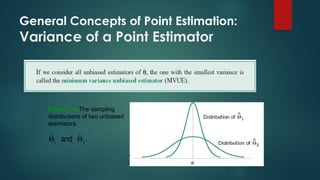
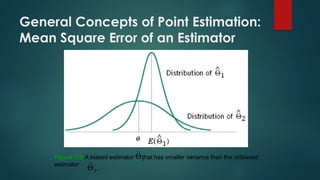
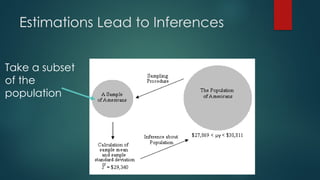
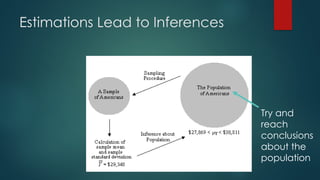
The document discusses statistical inference, which involves methods for making conclusions about a population based on sampled data. It explains parameter estimation, including the process of selecting samples and calculating sample statistics to estimate population parameters, and highlights the central limit theorem's role in assessing sampling distributions. Key concepts include unbiased estimators, consistency, and the importance of sound statistical practices to ensure valid estimations.











![7.2 Sampling Distributions and the
Central Limit Theorem
Figure 7-1
Distributions of
average scores from
throwing dice.
[Adapted with
permission from
Box, Hunter, and
Hunter (1978). ]](https://image.slidesharecdn.com/samplingdistributionandpointestimationofparameters-copy-240809074522-e8bb7502/85/SAMPLING-DISTRIBUTION-AND-POINT-ESTIMATION-OF-PARAMETERS-Copy-pptx-15-320.jpg)