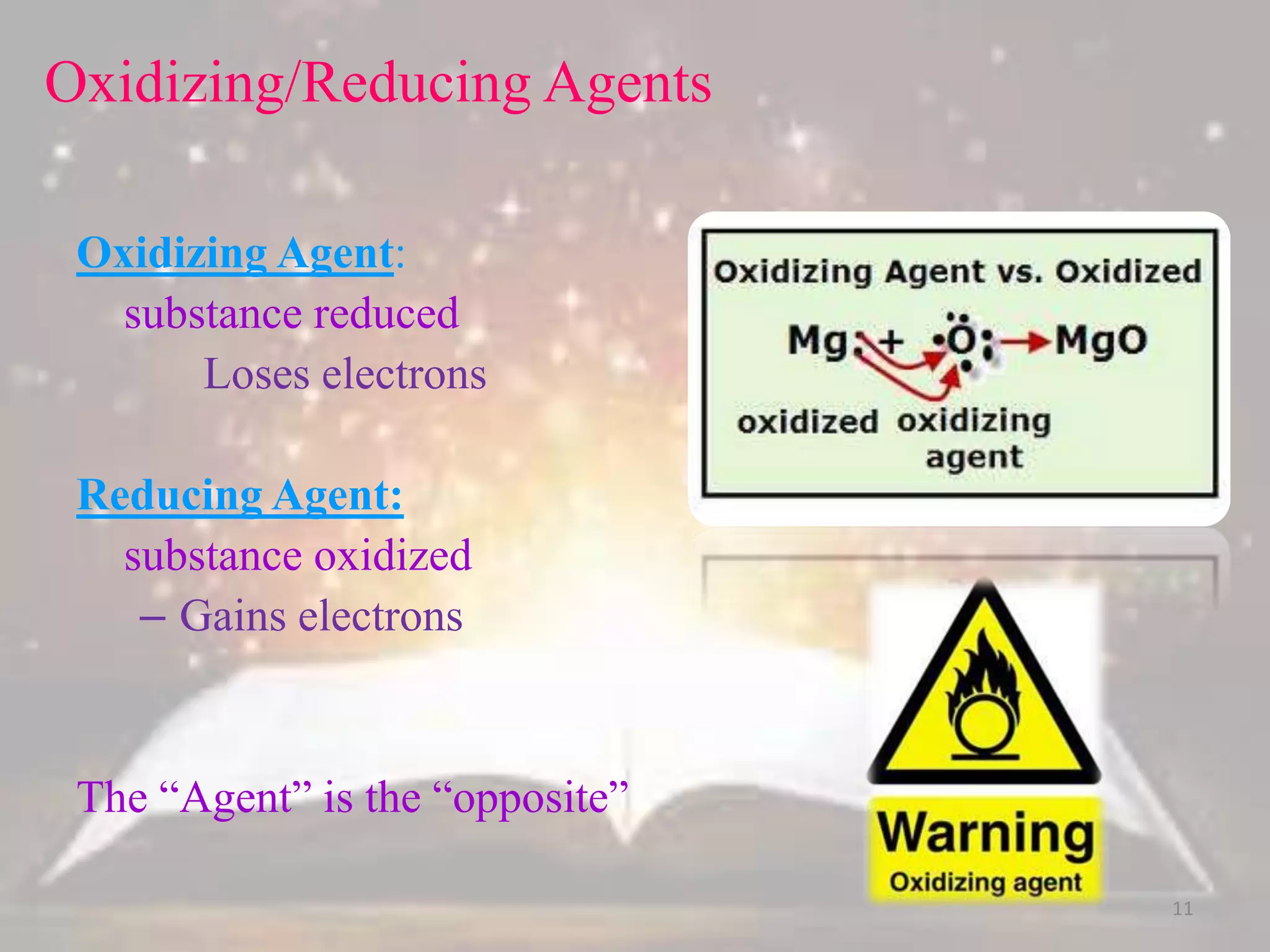
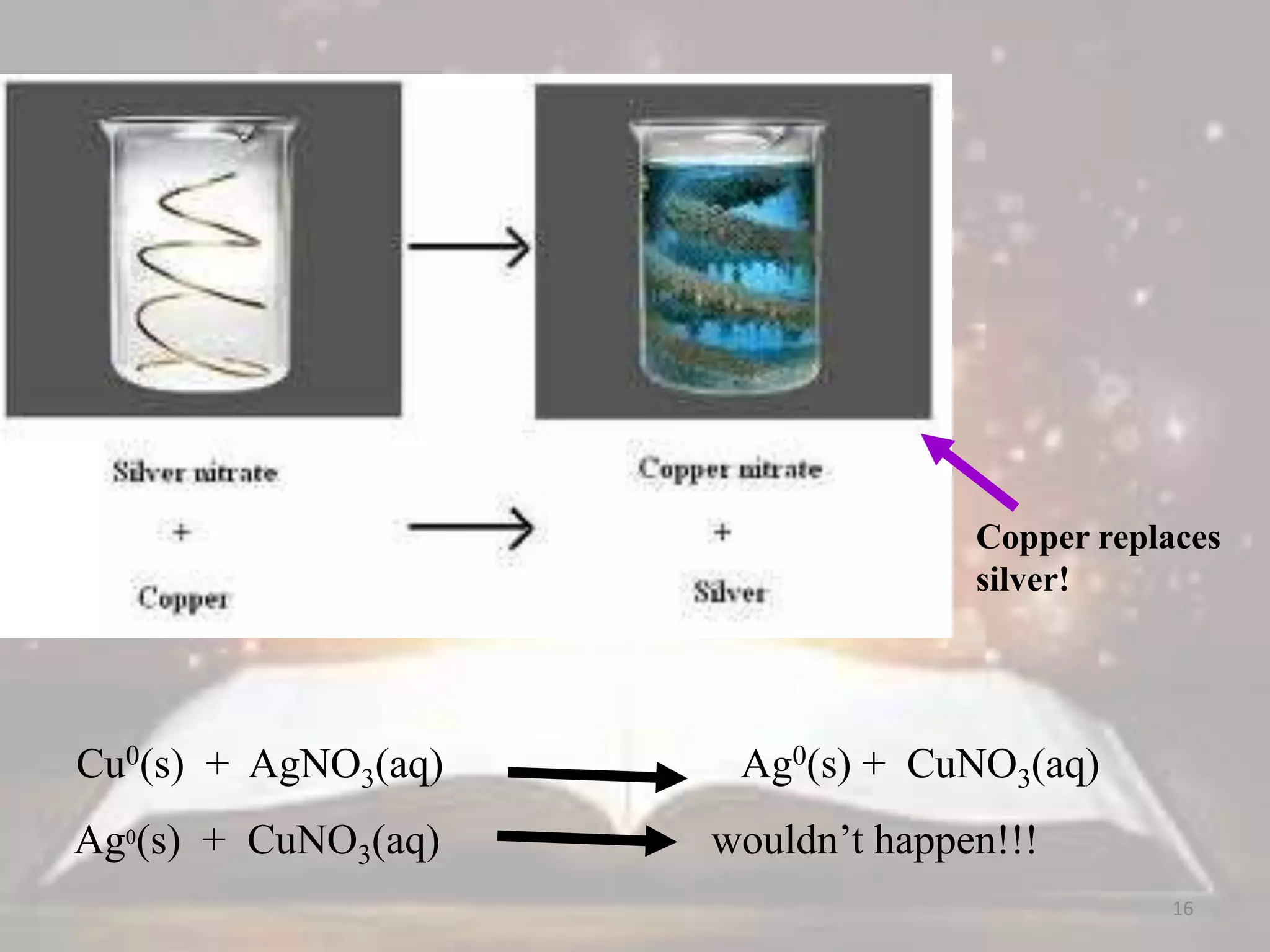
This document discusses oxidation-reduction (redox) reactions. It defines oxidation as the loss of electrons and reduction as the gain of electrons. Redox reactions always involve a transfer of electrons between reactants. The key principles are: 1. Oxidation and reduction always occur together in a redox reaction. 2. The total number of electrons lost must equal the total number of electrons gained to satisfy the conservation of charge. 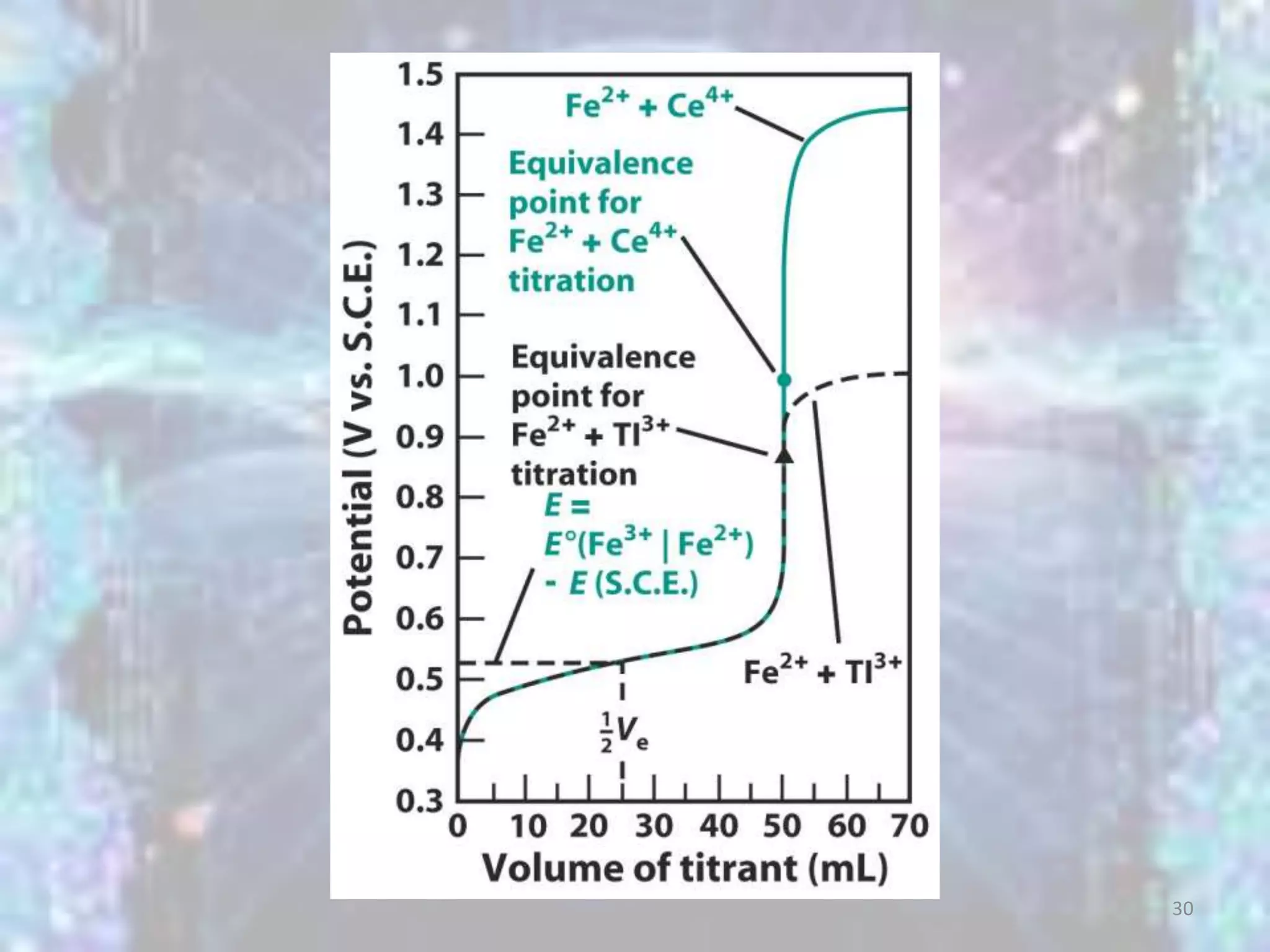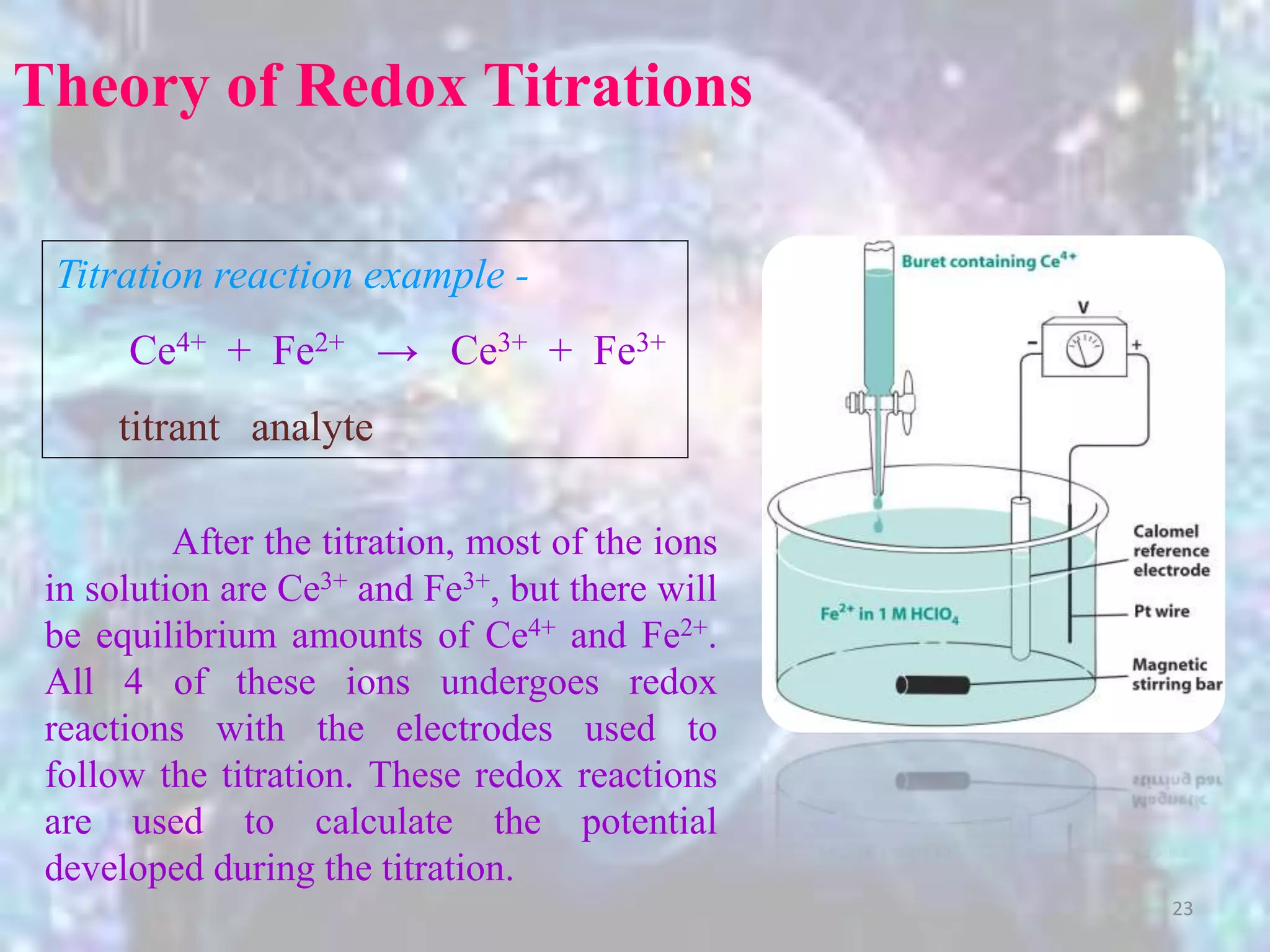3. Redox titrations can be used to determine the concentration of an unknown substance and rely on a redox reaction between a titrant and analyte with an indicator or potentiometer used to find the endpoint.

1. 1

2. 2

3. Oxidation
Original definition:
When substances combined with oxygen.
Ex:
All combustion (burning) reactions
CH4(g) + 2O2(g) CO2(g) + 2H2O(l)
All “rusting” reactions
4Fe(s) + 3O2(g) 2Fe2O3(s)
3

4. Reduction
Original Definition:
Reaction where a substance “gave up” oxygen
is called “reductions” because they produced
products that were “reduced” in mass because gas
escaped.
Ex:
2Fe2O3(l) + 3C(s) 4Fe(l) + 3CO2(g)
4

5. Oxidation/Reduction
Deals with movement of ELECTRONS
during a chemical reaction.
(Oxygen doesn’t have to be present)
5

6. Electron Transfer Reactions:
Oxidation: LOSS of one or more electrons
Reduction: GAIN of one or more electrons
6

7. Electron Transfer Reactions
Oxidation & reduction always occur together.
Electrons travel from what is oxidized towards
what is reduced.
One atom loses e-, the other gains e-
7

8. Redox Reactions:
ALWAYS involve changes in charge
A competition for electrons between atoms!
8

9. Remember!!
9

10. Conservation of “Charge”
Total electrons lost = Total electrons gained
10

11. Oxidizing/Reducing Agents
Oxidizing Agent:
substance reduced
Loses electrons
Reducing Agent:
substance oxidized
– Gains electrons
The “Agent” is the “opposite”
11

12. Redox or Not Redox
(that is the question…)
Redox Reactions: must have atoms changing in charge.
Not all reactions are redox.
Easy way to spot a redox reaction!!!
Look for elements entering and leaving compounds.
12

13. Applications of Redox Reactions
Corrosion of Metals
the metal gets oxidized
forming metal oxides on
the surface
Prevention: Use paint, oil,
plating or attach to negative
terminal of a battery.
Gold doesn’t
rust…Why? 13

14. Photograph Development involves oxidation and
reduction of silver atoms and ions
14

15. Bleach acts on
stains by oxidizing
them, getting reduced
in the process
Explosives form
neutral gases like N2
from compounds!
15

16. Copper replaces
silver!
Cu0(s) + AgNO3(aq) Ag0(s) + CuNO3(aq)
Ag0(s) + CuNO3(aq) wouldn’t happen!!!
16

18. Principle:
Redox titrations are based on a reduction-
oxidation reaction between an oxidizing and reducing
agent.
A potentiometer or redox indicator is usually
used to determine the endpoint of the titration.

20. Nernst Equation
The equation gives the relationship between the
electrode potential(E) of any given redox system,
concentration of oxidised/ reduced forms and shows the
dependence of electrode potential on concentration.
n = total number of moles electrons being transferred
R = gas constant = 8.314 Joules/deg.mol
F= Faraday’s constant = 96500 coulombs
T= Absolute temperature = 298ºC 20

21. The concentration of dissolved ions can affect voltage.
Greater concentration of reactant ions (see net)
increases the overall voltage.

23. Theory of Redox Titrations
Titration reaction example -
Ce4+ + Fe2+ → Ce3+ + Fe3+
titrant analyte
After the titration, most of the ions
in solution are Ce3+ and Fe3+, but there will
be equilibrium amounts of Ce4+ and Fe2+.
All 4 of these ions undergoes redox
reactions with the electrodes used to
follow the titration. These redox reactions
are used to calculate the potential
developed during the titration.
23

24. Saturated Calomel Reference Electrode half-reaction:
2Hg(l) + 2Cl-(aq) = Hg2Cl2(s) + 2e- Eo = 0.241 V
Pt electrode half-reactions:
Fe3+ + e- = Fe2+ Eo' = 0.767 V*
Ce4+ + e- = Ce3+ Eo' = 1.70 V*
The net cell reaction can be described in two equivalent ways:
2Fe3+ + 2Hg(l) + 2Cl- = 2Fe2+ + Hg2Cl2(s)
2Ce4+ + 2Hg(l) + 2Cl- = 2Ce3+ + Hg2Cl2(s)
* formal potential in 1.0 M HClO424

25. E = E+ - E-
0.241V
][Fe
][Fe
log0.0592-0.767V 3
2






 

Nernst equation for
Fe3+ + e- = Fe2+ (n=1)
Eo = 0.767V
E- = Sat'd
Calomel
Electrode voltag
(ESCE)
][Fe
][Fe
log0.0592-0.526V 3
2



Before the Equivalence Point
It's easier to use the Fe half-reaction because we know how
much was originally present and how much remains for each aliquot of
added titrant (otherwise, using Ce would require a complicated
equilibrium to solve for).
25

26. We're only going to calculate the potential at the half-
equivalence point where [Fe2+] = [Fe3+]:
][Fe
][Fe
log0.0592-0.526VE 3
2
1/2 


0
E1/2 = 0.526V or more generally for the half-equivalence point:
E1/2 = E+ - E- where E+ = Eo (since the log term went to zero)
and E- = ESCE
E1/2 = Eo - ESCE
26

27. At the Equivalence Point
Ce3+ + Fe3+ = Ce4+ + Fe2+ (reverse of the titration reaction)
titrant analyte
from the reaction stoichiometry, at the eq. pt. -
[Ce3+] = [Fe3+]
[Ce4+] = [Fe2+]
the two ½ reactions are at equilibrium with the Pt electrode -
Fe3+ + e- = Fe2+
Ce4+ + e- = Ce3+
so the Nernst equations are -
][Fe
][Fe
log0.0592-EE 3
2
0
Fe 



][Ce
][Ce
log0.0592-EE 4
3
o
Ce 



27

28. adding the two equations
together gives -
][Ce
][Ce
log0.0592-
][Fe
][Fe
log0.0592-EE2E 4
3
3
2
o
Ce
o
Fe 





][Fe
][Fe
log0.0592-EE 3
2
0
Fe 



][Ce
][Ce
log0.0592-EE 4
3
o
Ce 



][Ce
][Ce
][Fe
][Fe
log0.0592-EE2E 4
3
3
2
o
Ce
o
Fe 





and since [Ce3+] = [Fe3+] and [Ce4+] = [Fe2+]
][Fe
][Fe
][Fe
][Fe
log0.0592-EE2E 2
3
3
2
o
Ce
o
Fe 





28

29. ][Fe
][Fe
][Fe
][Fe
log0.0592-EE2E 2
3
3
2
o
Ce
o
Fe 





o
Ce
o
Fe
EE2E 
1.23V
2
2.467
2
1.700.767
2
EE
E
o
Ce
o
Fe





More generally, this is the cathode
potential at the eq. pt. for any redox reaction
where the number of electrons in each half
reaction is equal.
2
EE
E
00
analytetitrant


Ee.p. = E+ - E- = E+ - ESCE = 1.23 - 0.241 = 0.99V
29

30. 30

31. Equivalence Point Potentials
Use these equations with Standard Reduction Potentials!
1. Equal number of electrons
2. Unequal number of electrons (m = #e's cathode ½ rxn, n = #e's
anode ½ rxn)
2
EE
E
0
analyte
0
titrant


nm
nEmE
E
00
analytetitrant



31

32. Examples
1. Equal number of electrons
Fe2+ + Ce4+ = Fe3+ + Ce3+ in 1 M HClO4
titrant
2. Unequal number of electrons
Sn4+ + 2Cr2+ = Sn2+ + 2Cr3+ in 1 M HCl
titrant
32

33. 33

34. Detection of endpoint:
Potentiometery
Indicator method
Self indicator
Internal indicators
External indicators
Redox indicators

35. KMnO4 is its own indicator, and electrodes can be used also, in
which case the eq. pt. is obtained by calculating the 2nd derivative.
Otherwise, an indicator is chosen that changes color at the eq. pt.
potential.
35

36. 36