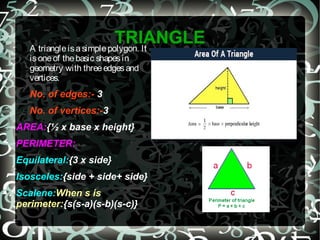
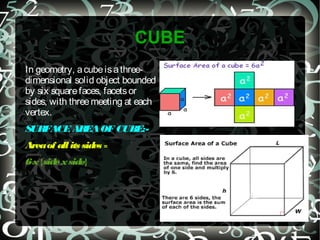
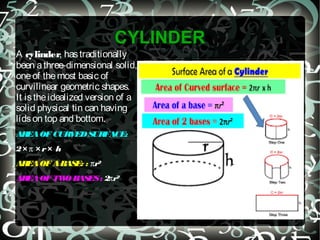
This document is a math project on mensuration submitted by Indira Singh of class VIIIA. It defines mensuration as the branch of mathematics dealing with measuring the areas and volumes of geometric figures. It then provides definitions of area and perimeter. The bulk of the document discusses different geometric shapes like squares, rectangles, triangles, parallelograms, trapezoids, rhombuses, cubes, cuboids and cylinders. It provides the number of sides, vertices, formulas to calculate the area and perimeter of two-dimensional shapes. It also gives the formulas to calculate the surface area and volume of three-dimensional solids.

1. BIRLA BALIKA VIDYAPEETH
MATHS PROJECT 2018
Submitted by :
Indira Singh
Class : VIIIA
Roll no:-7
Submitted to :
Mrs. Rini Abrahm

2. CHAPTER 11
MENSURATION
What is mensuration in mathematics?
Mensuration is a branch in mathematics which deals
with measurement of areas and volumes of various
geometrical figures. Figures such as
cubes,cuboid,cones,cylinders and spheres have
volume and area. Mensuration deals with
development of formulas to measure the areas and
volume.

3. INTRODUCTION
● PERIMETER OF CLOSED
FIGURE
● AREA OF
QUADRILATERAL AND
POLYGONS
●
SURFACE AREAS OF
SOLIDS
● VOLUME OF SOLIDS

4. DEFINATIONS
● AREA :-The amount of space inside the boundary
of a two dimensional shape .
● PERIMETER :-The amount of space outside the
boundary of a two dimensional shape .

5. SQUARE
Square, regular quadrilateral of all
four sidesof equal length and angles.
Itsoppositesidesareparallel and its
diagonalsperpendicularly bisect
each other,and areof equal length. A
quadrilateral isasquareonly if it
possesboth the propertiesoneof a
rhombus{FOUR EQUAL SIDES} and of
rectangles{FOUR EQUAL ANGLES}.
No. of edges:- 4
No. of vertices:-4
AREA:{side x side}
PERIMETER: {4 x side}

6. RECTANGLE
In rectangle,all anglesareright
angles. Thediagonalsbisect each
other and areequal in length. A
rectangleisalso parallelogram
(OPPOSITE SIDES ARE PARALLEL TO
EACH OTHER) .
No. of edges:- 4
No. of vertices:-4
AREA:{length x breadth}
PERIMETER:2{length+breadth}

7. TRIANGLEA triangleisasimplepolygon. It
isoneof thebasic shapesin
geometry with threeedgesand
vertices.
No. of edges:- 3
No. of vertices:-3
AREA:{½ x base x height}
PERIMETER:
Equilateral:{3 x side}
Isosceles:{side + side+ side}
Scalene:When s is
perimeter:{s(s-a)(s-b)(s-c)}

8. PARALLELOGRAM
A parallelogram isaquadrilateral
with oppositesidesequal and parallel
to each other. It hasoppositeequal
angles.Parallelogramsincludesall
rhombi and rhomboidsthusincludes
all rectangles.
No. of edges:- 4
No. of vertices:-4
AREA:{½ x base x height}
PERIMETER:{sum of all its
sides}

9. TRAPEZIUM
In Euclidean geometry, aconvex
quadrilateral with at least onepair of
parallel sidesisreferred to asatrapezium
in English outsideNorth America. The
parallel sidesarecalled thebasesof a
trapezium and theother two sidesare
called legsor lateral sides.
No. of edges:- 4
No. of vertices:-4
AREA:{½(sum of its sides) x
height}
PERIMETER:{sum of all its
sides}

10. RHOMBUS
Rhombushasall itsfour sidesof
equal length. Thediagonalsof a
rhombusperpendicularly bisect each
other. Informally:'apushover
square'.
No. of edges:- 4
No. of vertices:-4
AREA:½ x {product of its
diagonals}
PERIMETER:{sum of all its
sides}

11. CUBE
In geometry, acubeisathree-
dimensional solid object bounded
by six squarefaces, facetsor
sides, with threemeeting at each
vertex.
SURFACEAREAOFCUBE:-
Areaof allits sides =
6x{sidexside}

12. CUBOID
A cuboid isabox-shaped object
madeof six facesthat all meet at 90-
degreeangles. A cuboid shapecan
also beacubeif all sidesarethe
samelength{NOT ALL CUBOIDS ARE
CUBES}.
SURFACEAREAOFCUBOID:-
AREAOFALLITSFACES=
2{lb+ bh+ hl}

13. CYLINDER
A cylinder, hastraditionally
been athree-dimensional solid,
oneof themost basic of
curvilinear geometric shapes.
It istheidealized version of a
solid physical tin can having
lidson top and bottom.
AREAOFCURVEDSURFACE:
2× π × r× h
AREAOFABASE: : πr²
AREAOFTWO BASES: 2πr²

14. VOLUME OF
SOLIDS

15. CUBE
● A cubehassix squarefaces.
● Thelength of each squareface
isequal.
VOLUMEOF CUBE :
Lengthx length x length
Or
L3

16. CUBOID
● A cuboid also has6 faces.
● However,they arenot
equal in length.
VOLUMEOF CUBOID:
Lengthx widthx height

17. CYLINDER
A cylinderistheidealized
version of asolid physical tin can
having lidson top and bottom.
VOLUMEOFCYLINDER:
πr²h

18. HOPE YOU LIKED IT