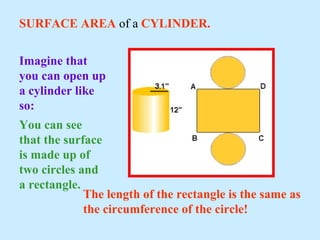
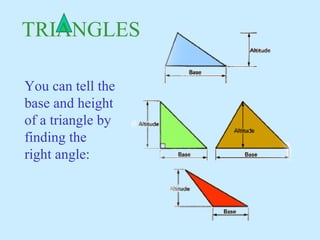
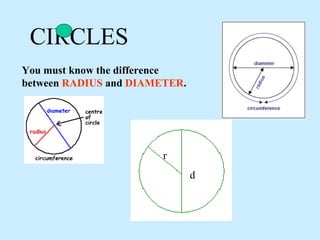
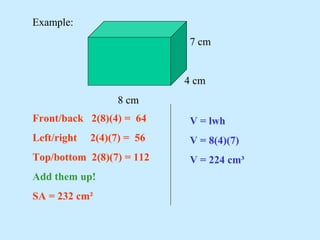
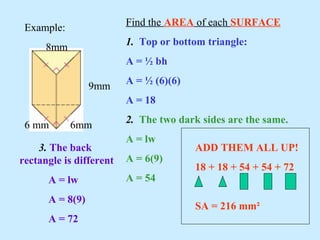
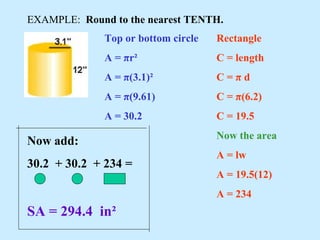
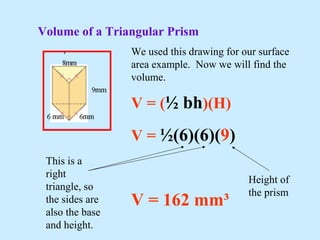
1) The document provides formulas for calculating the surface area and volume of basic geometric shapes like rectangles, triangles, circles, cylinders, prisms, and triangular prisms. 2) It explains how to identify the key dimensions needed to substitute into the formulas, like finding the radius, diameter, height, and base/length of an object. 3) Examples are provided to demonstrate applying the formulas step-by-step to calculate surface areas and volumes.

1. Geometry
Formulas:
Surface AreaSurface Area
& Volume& Volume

2. A formula is just a set of instructions.
It tells you exactly what to do!
All you have to do is look at the
picture and identify the parts.
Substitute numbers for the variables
and do the math. That’s it! 

3. Let’s start in the beginning…
Before you can do surface area or volume,
you have to know the following formulas.
Rectangle A = lw
Triangle A = ½ bh
Circle A = π r²
C = πd

4. You can tell the
base and height
of a triangle by
finding the
right angle:
TRIANGLES

5. CIRCLES
You must know the difference
between RADIUS and DIAMETER.
r
d

6. Let’s start with a rectangular prism.
Surface area can be done using the formula
SA = 2 lw + 2 wl + 2 lw OR
Either method will gve you the same answer.
you can find the area
for each surface and
add them up.
Volume of a rectangular prism is V = lwh

7. Example:
7 cm
4 cm
8 cm
Front/back 2(8)(4) = 64
Left/right 2(4)(7) = 56
Top/bottom 2(8)(7) = 112
Add them up!
SA = 232 cm²
V = lwh
V = 8(4)(7)
V = 224 cm³

8. To find the surface
area of a triangular
prism you need to be
able to imagine that
you can take the
prism apart like so:
Notice there are TWO congruent triangles
and THREE rectangles. The rectangles
may or may not all be the same.
Find each area, then add.

9. Example:
8mm
9mm
6 mm 6mm
Find the AREA of each SURFACE
1. Top or bottom triangle:
A = ½ bh
A = ½ (6)(6)
A = 18
2. The two dark sides are the same.
A = lw
A = 6(9)
A = 54
3. The back
rectangle is different
A = lw
A = 8(9)
A = 72
ADD THEM ALL UP!
18 + 18 + 54 + 54 + 72
SA = 216 mm²

10. SURFACE AREA of a CYLINDER.
You can see
that the surface
is made up of
two circles and
a rectangle.
The length of the rectangle is the same as
the circumference of the circle!
Imagine that
you can open up
a cylinder like
so:

11. EXAMPLE: Round to the nearest TENTH.
Top or bottom circle
A = πr²
A = π(3.1)²
A = π(9.61)
A = 30.2
Rectangle
C = length
C = π d
C = π(6.2)
C = 19.5
Now the area
A = lw
A = 19.5(12)
A = 234
Now add:
30.2 + 30.2 + 234 =
SA = 294.4 in²

12. There is also a formula to find surface area of a cylinder.
Some people find this way easier:
SA = 2πrh + 2πr²
SA = 2π(3.1)(12) + 2π(3.1)²
SA = 2π (37.2) + 2π(9.61)
SA = π(74.4) + π(19.2)
SA = 233.7 + 60.4
SA = 294.1 in²
The answers are REALLY close, but not exactly the same.
That’s because we rounded in the problem.

13. Find the radius and height of the cylinder.
Then “Plug and Chug”…
Just plug in the numbers then do the math.
Remember the order of operations and you’re
ready to go.
The formula tells you what to do!!!!
2πrh + 2πr² means multiply 2(π)(r)(h) + 2(π)(r)(r)

14. Volume of Prisms or Cylinders
You already know how to find the volume of a
rectangular prism: V = lwh
The new formulas you need are:
Triangular Prism V = (½ bh)(H)
h = the height of the triangle and
H = the height of the cylinder
Cylinder V = (πr²)(H)

15. Volume of a Triangular Prism
We used this drawing for our surface
area example. Now we will find the
volume.
V = (½ bh)(H)
V = ½(6)(6)(9)
V = 162 mm³
This is a
right
triangle, so
the sides are
also the base
and height.
Height of
the prism

16. Try one:
Can you see the
triangular bases?
V = (½ bh)(H)
V = (½)(12)(8)(18)
V = 864 cm³
Notice the prism is on
its side. 18 cm is the
HEIGHT of the prism.
Picture if you turned it
upward and you can
see why it’s called
“height”.

17. V = (πr²)(H)
V = (π)(3.1²)(12)
V = (π)(3.1)(3.1)(12)
V = 396.3 in³
Volume of a Cylinder
We used this drawing for our
surface area example. Now we will
find the volume.
optional
step!

18. Try one:
10 m
d = 8 m
V = (πr²)(H)
V = (π)(4²)(10)
V = (π)(16)(10)
V = 502.7 m³
Since d = 8,
then r = 4
r² = 4² = 4(4) = 16

19. Here are the formulas you will need to know:
A = lw SA = 2πrh + 2πr²
A = ½ bh V = (½ bh)(H)
A = π r² V = (πr²)(H)
C = πd
and how to find the surface area of a prism
by adding up the areas of all the surfaces