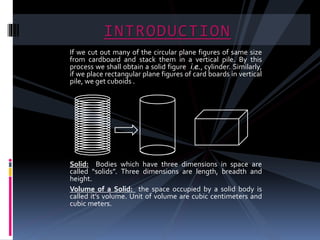
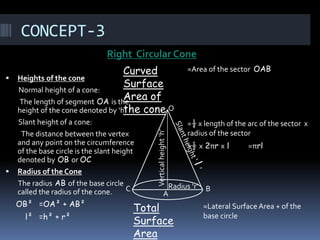
The document discusses different geometry concepts related to mensuration including cubes, cuboids, cylinders, cones, spheres and hemispheres. It defines key terms like total surface area, lateral surface area and volume. Formulas are provided to calculate surface areas and volumes of cubes, cuboids, cylinders, cones, spheres and hemispheres. Examples are given to illustrate concepts like hollow cylinders and spherical shells.

1. BY: ARCHAN CHATTERJEE
ROLL: 04 CLASS: IX ‘C’
Mensuration

2.  Introduction.
Total Surface Area and Lateral Surface Area of
Cuboids & Cubes.
Volume of Cuboids & Cubes.
Total Surface Area and Lateral Surface Area of
Right circular cylinder and hollow cylinder.
Volume of Right circular cylinder and hollow
cylinder.
Total Surface Area and Lateral Surface Area of
Right Circular Cone.
Volume of Right Circular Cone.
Total Surface Area and Lateral Surface Area of
Sphere and Hemispheres.
Volume of Sphere and Hemispheres.
Topics to be discussed

3. If we cut out many of the circular plane figures of same size
from cardboard and stack them in a vertical pile. By this
process we shall obtain a solid figure i.e., cylinder. Similarly,
if we place rectangular plane figures of card boards in vertical
pile, we get cuboids .
Solid: Bodies which have three dimensions in space are
called “solids”. Three dimensions are length, breadth and
height.
Volume of a Solid: the space occupied by a solid body is
called it’s volume. Unit of volume are cubic centimeters and
cubic meters.
INTRODUCTION

4. CONCEPT-1
CUBOIDS
 Total Surface Area
We know that the outer surface of a
cuboid is made up of six is made up of six
rectangles and the area of each
rectangle is the product of its length and
breadth.
 Lateral Surface Area
We find the area of four faces
leaving the faces and the top
faces then the area of these
four faces is called the lateral
surface area of the figure.
Lateral surface area of the
cuboid is = 2 { lh + bh }
I
III
II
Area of I rectangle =l x h
Area of back of I rectangle =l x h
Area of II rectangle =b x h
Area of back of II rectangle =b x h
Area of III rectangle =l x h
Area of bottom of III rectangle =l x h
Surface Area of a cuboid =Area of six rectangles
=lb + lb + bh + bh + lh + lh
=2lb + 2bh + 2lh
=2 {lb + bh + lh}

5. CONCEPT-1
Cubes
 Total Surface Area
A Cube is a cuboid whose length,
breadth and height are equal. If
each of the edges of a cube are
taken as ‘a’ then
 Lateral Surface Area
We find the area of four faces
leaving the faces and the top faces
then the area of these four faces is
called the lateral surface area of the
figure.
Lateral Surface Area
of cube = 4a²
The surface
area of the cube
=2{a x a + a x a + a x a}
=2{a² + a² + a²} = 2 x 3a²
Surface Area
of the cube
=6a²
a

6. VOLUMES
Volume of a Cube Volume of a cuboid
If we cut some rectangular sheets from
cardboard and place it one over the
other, if we place rectangular sheet
vertically in pile, it becomes a
cuboid.
If the area of each rectangle is ‘A’ and
the height up to which the
rectangles are stacked is ‘h’, then
Volume of the cuboid = Area of sheet x height
V = A x h
A = l x b
V = ( l x b ) x h
Volume of the cuboid = length x breadth x height
Volume of a cube =edge x edge x edge
= a³
A Cube is a cuboid whose length,
breadth and height are equal. If each
of the edges of a cube are taken as
‘a’ then

7. CONCEPT-2
Right circular cylinder
 Total Surface Area
An object having a curved surface and
congruent circular cross section is called a
circular cylinder. If we cut a number of
circular sheets and stack them in vertical pile
we will get a right circular cylinder.We shall
call the right circular cylinder as cylinder.
If a cylinder is hollow then it will be made up of
two geometrical figure rectangle and two
circles.
Total Surface area= Area of the rectangle +
Area of two circles
= 2πrh + πr² + πr²
= 2πrh + 2πr²
= 2πr ( h + r )
 Lateral Surface Area
A D
B C
2πr
2πr
h h
Area= (2πr) x h
= 2πrh
πr²
πr²
Lateral Surface of a
cylinder
= Circumference of the
base x Height
= 2πr x h
= 2πrh

8. CONCEPT-2
Hollow Cylinder
Hollow cylinder is a solid bounded by
two co-axial cylinders of the same
height and different radii.
Area of each end = πR² - πr² = π (R² - r²)
Curved Surface Area of the Hollow Cylinder
=External Surface + Internal Surface
=2πRh + 2πrh = 2πh(R + r)
Total Surface Area of the
hollow cylinder
= Curved Surface Area+2Area
of the Base
=2πRh + 2πrh + 2π(R²-r²)
=2π( R+r ) ( h+R-r)

9. VOLUMES
Volume of Solid Cylinder Volume of Hollow Cylinder
The space enclosed by a cylinder has
volume and this volume is known as
volume of a cylinder.
Volume of the
material of the hollow
cylinder
=External volume –
Internal volume
B
h
r
Volume of the cylinder =Area of the base x height
=(πr²) x h
Volume of the cylinder =πr²h
=πR²h – πr²h =πh(R² - r²)
h
R r

10. CONCEPT-3
Right Circular Cone
 Heights of the cone
Normal height of a cone:
The length of segment OA is the
height of the cone denoted by ‘h’
Slant height of a cone:
The distance between the vertex
and any point on the circumference
of the base circle is the slant height
denoted by OB or OC
 Radius of the Cone
The radius AB of the base circle
called the radius of the cone.
OB² =OA² + AB²
l² =h² + r²
B
A
Radius ‘r’
Verticalheight‘h’
C
O
Curved
Surface
Area of
the cone
=Area of the sector OAB
=½ x length of the arc of the sector x
radius of the sector
=½ x 2πr x l =πrl
Total
Surface
Area
=Lateral Surface Area + of the
base circle

11. VOLUMES
Volume of a Right Circular Cone
NOTE: Both the cone and cylinder are of same
height and same radius as well as same base.
The space enclosed by a cone has volume and
this volume is known as volume of a cone.
3 xVolumes of a cone = One volume of a right circular cylinder
Volume of a cone = 1/3Volume of a right circular cylinder
Volume of a cone =1/3πr²h
Volume of a
cone
=1/3πr
²h

12. CONCEPT-4
Sphere and Hemisphere
Sphere
A sphere is described as a set of all
those points in space which are
equidistant from a fixed point. The
fixed point is called the center of the
sphere and the constant distance is
called the radius.
Hemisphere
A plane passing through the centre of
a sphere divides the sphere into two
equal parts, each part of which is
called the hemisphere.
Surface Area of Sphere =4πr²
1. Curved Surface Area
of hemisphere.
=2πr²
2. Total Surface Area of
hemisphere
=2πr² + πr² =3πr²
Outer surface Area of a Spherical Shell =4πR²

13. VOLUMES
Different types of Spheres
Volume a Sphere =4/3πr³
Volume of the
hemisphere
=1/2 X Volume of a sphere
=1/2 X 4/3πr³ =2/3πr³
Volume of a hollow cylinder
Volume of the material =Volume of outer sphere –Volume of inner sphere
=4/3πR³ – 4/3πr³ =4/3π(R³ – r³)
R
r