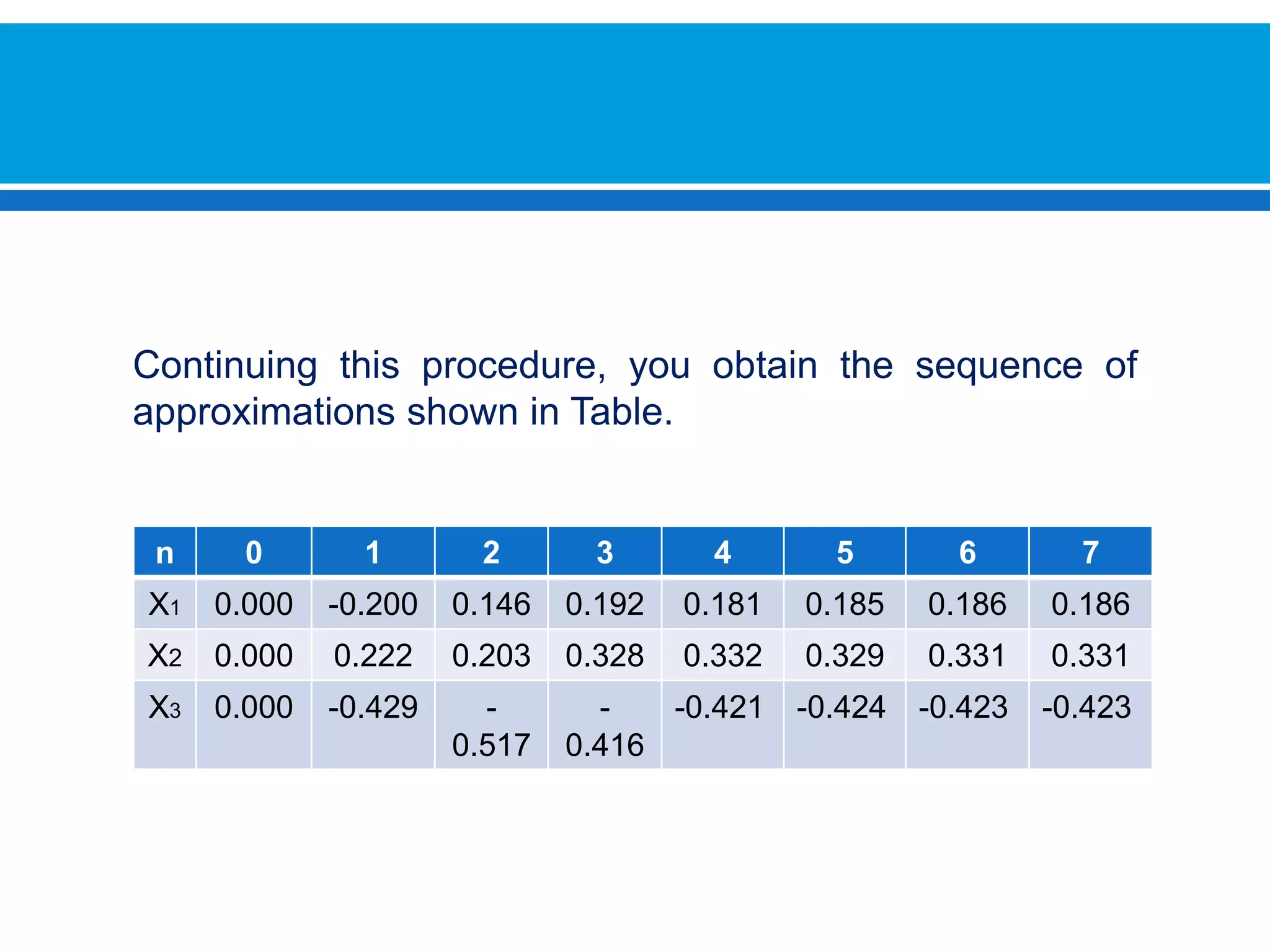
The document discusses iterative methods for solving systems of linear equations, including the Jacobi, Gauss-Seidel, and Gauss-Seidel relaxation methods. The Jacobi method works by rewriting the system in a form where the diagonal entries are isolated and computing successive approximations. The Gauss-Seidel method similarly computes approximations but uses the most recent values available at each step. Relaxation improves the Gauss-Seidel method's convergence by taking a weighted average of the current and previous iterations' results. Examples demonstrate applying the different methods to compute solutions.

1. ITERATIVESMETHODS

2. JACOBI METHODITERATIVESMETHODS

3. JACOBI METHODSuppose we are trying to solve a system of linear equation Mx= b. If we assume that the diagonal entries are non-zero (true if the matrix M is positive definite), then we may rewrite this equation as:Dx+ Moffx = bWhere:Dis the diagonal matrix containing the diagonal entries of M and Moff contains the off-diagonal entries of M. Because all the entries of the diagonal matrix are non-zero, the inverse is simply the diagonal matrix whose diagonal entries are the reciprocals of the corresponding entries of D.

4. Thus, we may bring the off-diagonal entries to the right hand side and multiply by D-1:x = D-1(b - Moffx) You will recall from the class on iteration, we now have an equation of the form x = f(x), except in this case, the argument is a vector, and thus, one method of solving such a problem is to start with an initial vector x0.

5. EXAMPLE Use the Jacobi method to approximate the solution of the following system of linear equations:Withinitialvalues:

6. Continue the iterations until two successive approximations are identical when rounded to three significant digits.Tobegin, writethesystem in theform:

7. As a convenient initial approximation. So, the first approximation is:

8. Continuing thisprocedure, youobtainthesequence of approximationsshown in Table.

9. Becausethelasttwocolumns in table are identical, you can concludethattothreesignificantdigitsthesolutionis:Forthesystem of linear equations given in example, theJacobimethodissaid ti converge. Thatis, repeated iterations succeed in producingapproximationthatiscorrecttothreesignificantdigits. As is generally true foriterativemethods, grateraccuracywouldrequire more iterations.

10. GAUSS-SEIDEL METHODITERATIVESMETHODS

11. GAUSS-SEIDEL METHODThe Gauss–Seidel method, also known as the Liebmann method or the method of successive displacement, is an iterative method used to solve a linear system of equations. It is named after the GermanmathematiciansCarl Friedrich Gauss and Philipp Ludwig von Seidel, and is similar to the Jacobi method. Though it can be applied to any matrix with non-zero elements on the diagonals, convergence is only guaranteed if the matrix is either diagonally dominant, or symmetric and positive definite.

12. First solve for the unknowns in order.Then we assume an initial value for [X(0)]We must remember that I always use the most recent value xi. This means that calculated values apply for the calculations are in the current iteration

13. Calculation of relative absolute error approximateThen find the correct answer when the maximum relative absolute error is approximately less than the specified tolerance for all unknowns.

14. EXAMPLE Solve the following system of equations:Matrixcoefficients:Withinitialvalues:

15. Let's see if the matrix is diagonally dominantSatisfy all inequalities, therefore the solution should converge using the Gauss Seidel.

16. Rewritingeachequation:Withinitialvalues:

17. Iteration1Theapproximaterelativeabsoluteerror:The approximate maximum relative absolute error after the first iteration is 100%.

18. Substituting the above values into the equations

19. Iteration 2Theapproximaterelativeabsoluteerror:The approximate maximum relative absolute error after the second iteration is 24.7%.

20. Substituting the above values into the equations

21. Iteration 3Theapproximaterelativeabsoluteerror:The approximate maximum relative absolute error after the second iteration is 8.9%.

22. Substituting the above values into the equations

23. Iteration 4Theapproximaterelativeabsoluteerror:The approximate maximum relative absolute error after the second iteration is 0.06%.

24. Theresultingsolutionis:Theexactsolutionis:

25. GAUSS-SEIDEL RELAXATION METHODGauss-SeidelITERATIVESMETHODS

26. GAUSS-SEIDEL RELAXATIONThe Gauss-Seidel method is a technique for solving the equations of the linear system of equationsAx = b one at a time in sequence, and uses previously computed results as soon as they are available,

27. There are two important characteristics of the Gauss-Seidel method should be noted. Firstly, the computations appear to be serial. Since each component of the new iterate depends upon all previously computed components, the updates cannot be done simultaneously as in the Jacobi method. Secondly, the new iterate depends upon the order in which the equations are examined. If this ordering is changed, the components of the new iterates (and not just their order) will also change.

28. In terms of matrices, the definition of the Gauss-Seidel method can be expressed as where the matrices D, -L and -U represent the diagonal, strictly lower triangular, and strictly upper triangular parts of, respectively. The Gauss-Seidel method is applicable to strictly diagonally dominant, or symmetric positive definite matrices .

29. IMPROVING THE CONVERGENCE USING RELAXATION SORThe relaxation represents a slight modification to the Gauss Seidel and this improves the convergence. Estimated after each new value of x, that value is changed by a weighted average of the results of previous and current iteration.Where w is a weighting factor that has a Valors between 0 and 2.

30. Example.Figure 5. The effect of freezing the boundary on several levels of a surface.

31. EXAMPLE Solve the following system of equations for Relaxation SOR:Withinitialvalues:With:

32. Rewritingeachequation:Withinitialvalues X1:

33. Iteration1

34. Iteration2

35. And we must make the followings iterations y and obtained:

36. If A is symmetric and positive definite, the Gauss-Seidel method converges.If A is symmetric and the matrix is the form:And is positive definite, the Jacobi method is convergent.CONVERGENCE OF ITERATIVES METHODS

37. If A is symmetric and positive definite, the relaxation method converges if and only if 0 < w <2.If w < 1 the method is named subrelajation and if w > 1, Overrelaxation.If A is symmetric, positive definite and tridiagonal, the optimal value of w for the convergence of the relaxation method is: where:Pj: The spectral radius of the matrix Jacobi iteration method.

38. http://www.google.com.co/imgres?imgurl=http://www.unavarra.es/personal/victor_dominguez/portMatlab.jpg&imgrefurl=http://www.unavarra.es/personal/victor_dominguez/libroMatlab.htm&usg=__g0H6VfxnJXinSq932hKACQW-4mE=&h=423&w=596&sz=61&hl=es&start=19&itbs=1&tbnid=qcEPT90K9KGOJM:&tbnh=96&tbnw=135&prev=/images%3Fq%3DGauss-Seidel%2Bcon%2Brelajaci%25C3%25B3n%26hl%3Des%26sa%3DG%26gbv%3D2%26tbs%3Disch:1http://www.ana.iusiani.ulpgc.es/metodos_numericos/document/apuntes/Parte_4.pdfBibliography