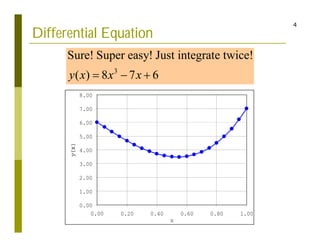
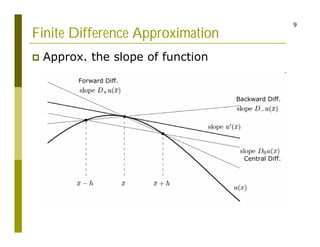
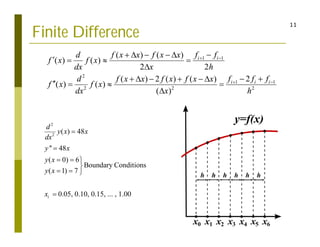
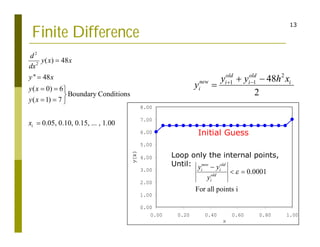
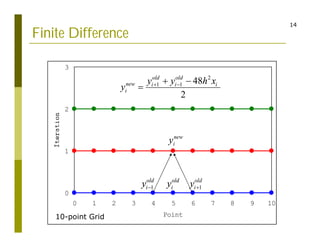
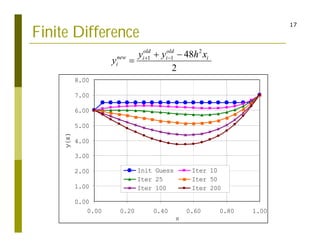
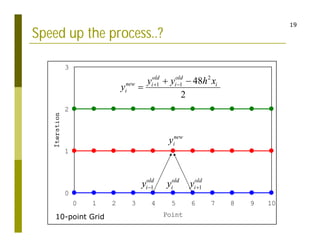
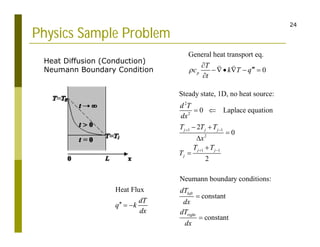
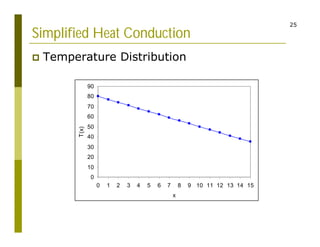
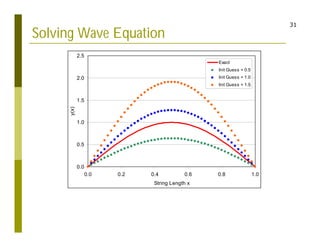
This document discusses finite difference methods for solving differential equations. It begins by introducing grid-based computation and finite difference approximations of derivatives. It then provides examples of solving differential equations using explicit and implicit finite difference schemes. The document discusses various approaches to implementing finite difference methods in code, including defining the domain, discretization, boundary conditions, and iteration procedures. It also gives examples of applying finite difference methods to problems in math, physics, and heat conduction.

1. 1
1
Programming, Computation, Simulation
Applications in Math & Physics
Finite Difference Methods
Syeilendra Pramuditya
Department of Physics
Institut Teknologi Bandung

2. 2
Grid-based Computation
 Euler-type Methods
 Differential equations
 Temporal domain (variation in time)
 Initial value problems
 Initial conditions
 Finite Difference Methods
 Differential equations
 Spatial domain (variation in space)
 Boundary value problems
 Dirichlet boundary conditions: value of solution at
boundaries
 Von Neumann boundary conditions: derivative of
solution at boundaries

3. 3
Differential Equation
2
2
( ) 48
'' 48
( 0) 6
Boundary Conditions
( 1) 7
Can you solve for ( )...?
d
y x x
dx
y x
y x
y x
y x


  

  

4. 4
Differential Equation
3
Sure! Super easy! Just integrate twice!
( ) 8 7 6
y x x x
  
0.00
1.00
2.00
3.00
4.00
5.00
6.00
7.00
8.00
0.00 0.20 0.40 0.60 0.80 1.00
x

5. 5
Differential Equation
2
2
( ) 5 ( ) 10 ( ) 10
5 10 10
( 0) 0
Boundary Conditions
( 1) 100
Can you solve for ( )...???
d d
y x y x y x x
dx dx
y y y x
y x
y x
y x
  
 
  
  

  

6. 6
Derivation from Taylor Series
 Forward difference equation

7. 7
Derivation from Taylor Series
 Backward difference equation

8. 8
Derivation from Taylor Series
 Central difference equation
Now substract this
From this

9. 9
Finite Difference Approximation
 Approx. the slope of function
Forward Diff.
Backward Diff.
Central Diff.

10. 10
Finite Difference Equations
 The Central Difference

11. 11
Finite Difference
1 1
2
1 1
2 2 2
( ) ( )
( ) ( )
2 2
2
( ) 2 ( ) ( )
( ) ( )
( )
i i
i i i
f f
d f x x f x x
f x f x
dx x h
f f f
d f x x f x f x x
f x f x
dx x h
 
 

    
   

 
     
   

2
2
( ) 48
'' 48
( 0) 6
Boundary Conditions
( 1) 7
0.05, 0.10, 0.15, ... , 1.00
i
d
y x x
dx
y x
y x
y x
x


  

  


12. 12
Finite Difference
1 1
2
2
1 1
2
1 1
'' 48
2
48
2 48
48
2
i i i
i
i i i i
i i i
i
y x
y y y
x
h
y y y h x
y y h x
y
 
 
 

 

  
 

1 1
2
1 1
2 2
( ) ( )
2
2
( ) ( )
i i
i i i
f f
d
f x f x
dx h
f f f
d
f x f x
dx h
 
 

  
 
  

13. 13
0.00
1.00
2.00
3.00
4.00
5.00
6.00
7.00
8.00
0.00 0.20 0.40 0.60 0.80 1.00
x
Finite Difference
Initial Guess
2
2
( ) 48
'' 48
( 0) 6
Boundary Conditions
( 1) 7
0.05, 0.10, 0.15, ... , 1.00
i
d
y x x
dx
y x
y x
y x
x


  

  

2
1 1 48
2
old old
new i i i
i
y y h x
y  
 

Loop only the internal points,
Until:
0.0001
For all points i
new old
i i
old
i
y y
y


 

14. 14
Finite Difference
0
1
2
3
0 1 2 3 4 5 6 7 8 9 10
Point
10-point Grid
old
i
y 1
old
i
y 
1
old
i
y 
old
i
y
1
old
i
y 
new
i
y
2
1 1 48
2
old old
new i i i
i
y y h x
y  
 


15. 15
Code Structure
 Define domain boundaries (x1 & xN)
 Define resolution
 Define number of points (xi)
 Calculate h or x
 Define initial guess for internal points
 Define boundary conditions  f(x1) & f(xN)
 Dirichlet BC
 Double Loop
 Inner loop  Update internal points using finite
difference equation
 Outer loop  Convergence check: how much the change
of each point is?
 Loop until iteration is converged
 No significant change for all points

16. 16
Code Output
Converged in 379 iterations.
0, 6
0.05, 5.65543
0.1, 5.31675
0.15, 4.98985
0.2, 4.68064
0.25, 4.39501
0.3, 4.1389
0.35, 3.91822
0.4, 3.73892
0.45, 3.60695
0.5, 3.5283
0.55, 3.50895
0.6, 3.55492
0.65, 3.67221
0.7, 3.8669
0.75, 4.14501
0.8, 4.51263
0.85, 4.97585
0.9, 5.54074
0.95, 6.21343
1, 7

17. 17
Finite Difference
2
1 1 48
2
old old
new i i i
i
y y h x
y  
 

0.00
1.00
2.00
3.00
4.00
5.00
6.00
7.00
8.00
0.00 0.20 0.40 0.60 0.80 1.00
x
Init Guess Iter 10
Iter 25 Iter 50
Iter 100 Iter 200

18. 18
Finite Difference
Max error = 1E-4  379 iterations to converged
0.00
1.00
2.00
3.00
4.00
5.00
6.00
7.00
8.00
0.00 0.20 0.40 0.60 0.80 1.00
x
Exact
Finite Diff.

19. 19
Speed up the process..?
0
1
2
3
0 1 2 3 4 5 6 7 8 9 10
Point
10-point Grid
old
i
y 1
old
i
y 
1
old
i
y 
old
i
y
1
old
i
y 
new
i
y
2
1 1 48
2
old old
new i i i
i
y y h x
y  
 


20. 20
Speed up the process..?
2
1 1 48
2
old old
new i i i
i
y y h x
y  
 

2
1 1 48
2
old new
new i i i
i
y y h x
y  
 

Jacobi Method
Gauss-Siedel Method
379 iterations  219 iterations
1.73X Speed up!

21. 21
Finite Difference: Example
1 1
2
1 1
2 2 2
( ) ( )
( ) ( )
2 2
2
( ) 2 ( ) ( )
( ) ( )
( )
i i
i i i
f f
d f x x f x x
f x f x
dx x h
f f f
d f x x f x f x x
f x f x
dx x h
 
 

    
  

 
     
  



5 10 10
(0) 0
( ) 100
0.0, 0.1, 0.2, ... , 1.0
i
y y y x
y
y n
x
 
  




22. 22
Finite Difference: Example
1 1 1 1
2
2
1 1
2
5 10 10
2
5 10 10
2
1 5 5
1 1 10
2 10 2 2
i i i i i
i i
i i i i
y y y x
y y y y y
y x
h h
h h
y y y h x
h
   
 
 
  
  
  
 
   
    
   
 
    
 
1 1
2
1 1
2 2
( ) ( )
2
2
( ) ( )
i i
i i i
f f
d
f x f x
dx h
f f f
d
f x f x
dx h
 
 

  
 
  

23. 23
Physics Sample Problem
General heat transport eq.
0
p
T
c k T q
t



   

 
2
2
1 1
2
1 1
Steady state, 1D, no heat source:
0 Laplace equation
2
0
2
Dirichlet boundary conditions:
constant
constant
j j j
j j
j
left
right
d T
dx
T T T
x
T T
T
T
T
 
 
 
 






Heat Diffusion (Conduction)
Dirichlet Boundary Condition

24. 24
Physics Sample Problem
General heat transport eq.
0
p
T
c k T q
t



   

 
2
2
1 1
2
1 1
Steady state, 1D, no heat source:
0 Laplace equation
2
0
2
Neumann boundary conditions:
constant
constant
j j j
j j
j
left
right
d T
dx
T T T
x
T T
T
dT
dx
dT
dx
 
 
 
 






Heat Diffusion (Conduction)
Neumann Boundary Condition
Heat Flux
dT
q k
dx
  

25. 25
Simplified Heat Conduction
 Temperature Distribution
0
10
20
30
40
50
60
70
80
90
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
x
T(x)

26. 26
Code Structure
START
Set Boundary Conditions
Set Initial Guess
Repeat
Calculate interior points
Convergence check
Update interior points
Until Converge
Print Output
1 1
2
old old
new i i
i
T T
T  


for all i
new old
i i
old
i
T T
T



= for all i
old new
i i
T T

27. 27
Physics Sample Problem
 Vibrating String
 Guitar, bass, violin, piano, etc
 Resonance frequency  standing wave with
two closed ends

28. 28
Physics Sample Problem
 The Wave Equation
2 2
2 2
2 2
2
2 2
( , ) ( , )
Exact solution ( , ) sin( )
Guessed solution by variable separation ( , ) ( ) ( )
( ) ( )
1 1
const.
( ) ( )
m
x t x t
T
t x
x t kx t
x t y x t
d y x d t
T
y x dx t dt
 

  
 


 
 

 
  
 
   
2
2
2
2 2
2
( )
( ) Temporal domain (SHM), requires initial conditions
( )
( ) Spatial domain, requires boundary conditions
Solve the y(x) by finite difference?
d t
t
dt
d y x
y x
dx T

 
 
  
  

29. 29
Solving Wave Equation
2 2
2
2
1 1
2
2
1 1
2 2
2
1 1
2 2
2
1 1
2 2
1 1 1 1
2 2
2
2
2
( )
( ) 0
2
0
2
0
2
2
2
2
i i i
i
i i i
i
i i
i i
i i
i
i i i i
i
d y x
y x
dx T
y y y
y
h T
y y y
y
h h T
y y
y y
h h T
y y
y
h h T
y y y y
y
h
h
T
h T
 
 
 
 
 
 
 
 
 
 
 
   
 
 
 

  

 
 

 
 
 
 
 
 


 
 
Now imagine how you would write the code..?
What are the inputs?

30. 30
Solving Wave Equation
 Input
 String tension, T
 String length, L
 String linear density, 
 Harmonic order, n

31. 31
Solving Wave Equation
0.0
0.5
1.0
1.5
2.0
2.5
0.0 0.2 0.4 0.6 0.8 1.0
String Length x
y(x)
Exact
Init Guess = 0.5
Init Guess = 1.0
Init Guess = 1.5