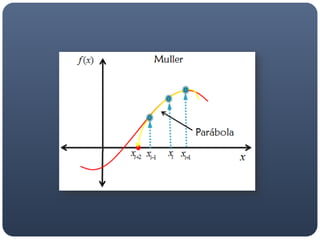
The Bairstow method and Muller method are techniques for calculating the roots of polynomials. The Bairstow method uses synthetic division to iteratively calculate the roots of a polynomial by dividing it by quadratic factors (x^2 - rx - s) until the remainder is zero. It obtains better approximations of r and s at each iteration to isolate the roots. The Muller method fits a parabola through three initial guesses to obtain the coefficients a, b, c of the quadratic formula. It then uses the quadratic formula to find the root, and iterates with new guesses to converge on more accurate roots. Both methods use iterative techniques to gradually converge on the real and complex roots of polynomials without

1. BAIRSTOW METHODMULLIER METHODDANIEL FERNANDO RODRIGUEZROOTS OF POLYNOMIALS

2. Bairstow MethodA method for calculating roots of polynomials can calculate peer (conjugated in the case of complex roots).Unlike Newton, calculate complex roots without having to make calculations with complex numbers. It is based on the synthetic division of the polynomial Pn (x) by the quadratic (x2 - rx - s).

3. Bairstow Method The synthetic division can be extended to quadratic factors:and even by multiplying the coefficients is obtained:

4. Bairstow MethodWe want to find the values of r and s that make b1 and b0 equal to zero since, in this case, the factor divided exactly quadratic polynomial. The first method works by taking an initial approximation (r0, s0) and generate approximations (rk, sk) getting better using an iterative procedure until the remainder of division by the quadratic polynomial (x2 - rkx - sk) is zero. The iterative procedure of calculation is based on the fact that both b1 and b0 are functions of r and s.

5. In developing b1 (rk, sk) and b0 (rk, sk) in Taylor series around the point (r *, s *), we obtain:It takes (r *, s *) as the point where the residue is zero and Δr = r * - rk, Δs = s * - sk. Then:Bairstow Method

6. Bairstow MethodBairstow showed that the required partial derivatives can be obtained from the bi by a second synthetic division between factor (x2 - r0x - s0) in the same way that the bi are obtained from the ai. The calculation is:

7. Thus, the system of equations can be writtenBairstow Method

8. Calculation of approximate error:When tolerance is reached estimated coefficientsrand s is used to calculate the roots:Bairstow Method

9. Bairstow MethodThen:When the resulting polynomial is of third order or more, the Bairstow method should be applied to obtain a resultant function of order 2.When the result is quadratic polynomial, defines two of the roots using the quadratic equation.When the final function is first order root is determined from the clearance of the equation.

10. MullerMethod Is based on the layout of a polynomial function specifically a parable with three initial values. Is to have the coefficients of a parabola passing through three points. These points are substituted into the quadratic formula to get the value where the parabola intersects the x-axis, ie, the approximate root.

12. The approach is facilitated by writing the parable in a convenient form:the parabola must pass through three points. These are evaluated as follows:

13. You can find the three unknown coefficients a, b, c and to two terms of the last equation are zero, f (x +1) = c, resulting in two equations with two unknowns

14. An algebraic manipulation allows you to find the remaining coefficients a, b. how to do this is to define the differences

15. These are replaced in the above equations and result:Where a and b are cleared and get:

16. Already known evaluate the quadratic coefficients: Evaluated to determine the sign: If D1 is developed further with the + quadratic, but is solved with the - sign

17. EXAMPLE:Use the muller method with initial values:To determine the root of the equation:

18. First evaluate the function to baseline:That are used to calculate:

19. These values are replaced in turn to find the values of a, b, cThen we find the term D major to determine the sign of the quadratic

20. As D1> D2 solve the quadratic with a positive sign. After the error is calculated accordingly to the Xi +1 xi +2 with the new variables:

21. Now for the new iterationXi-1 = Xi previousXi +1 = Xi previousXi +2 = Xi +1calculated

22. BIBLIOGRAPHYCHAPRA, Steven C. y CANALE, Raymond P.: Métodos Numéricos para Ingenieros. McGraw Hill 2002.