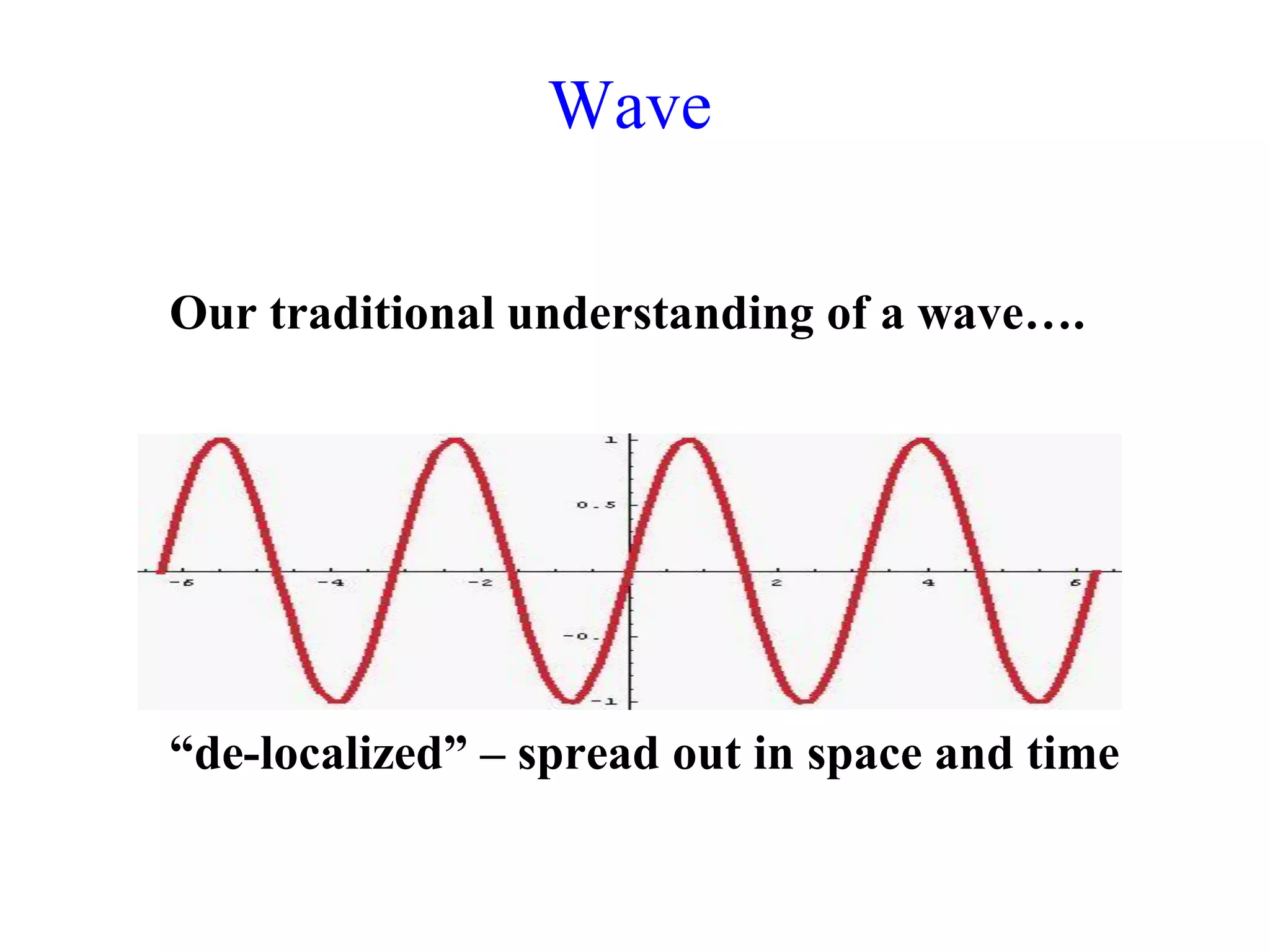
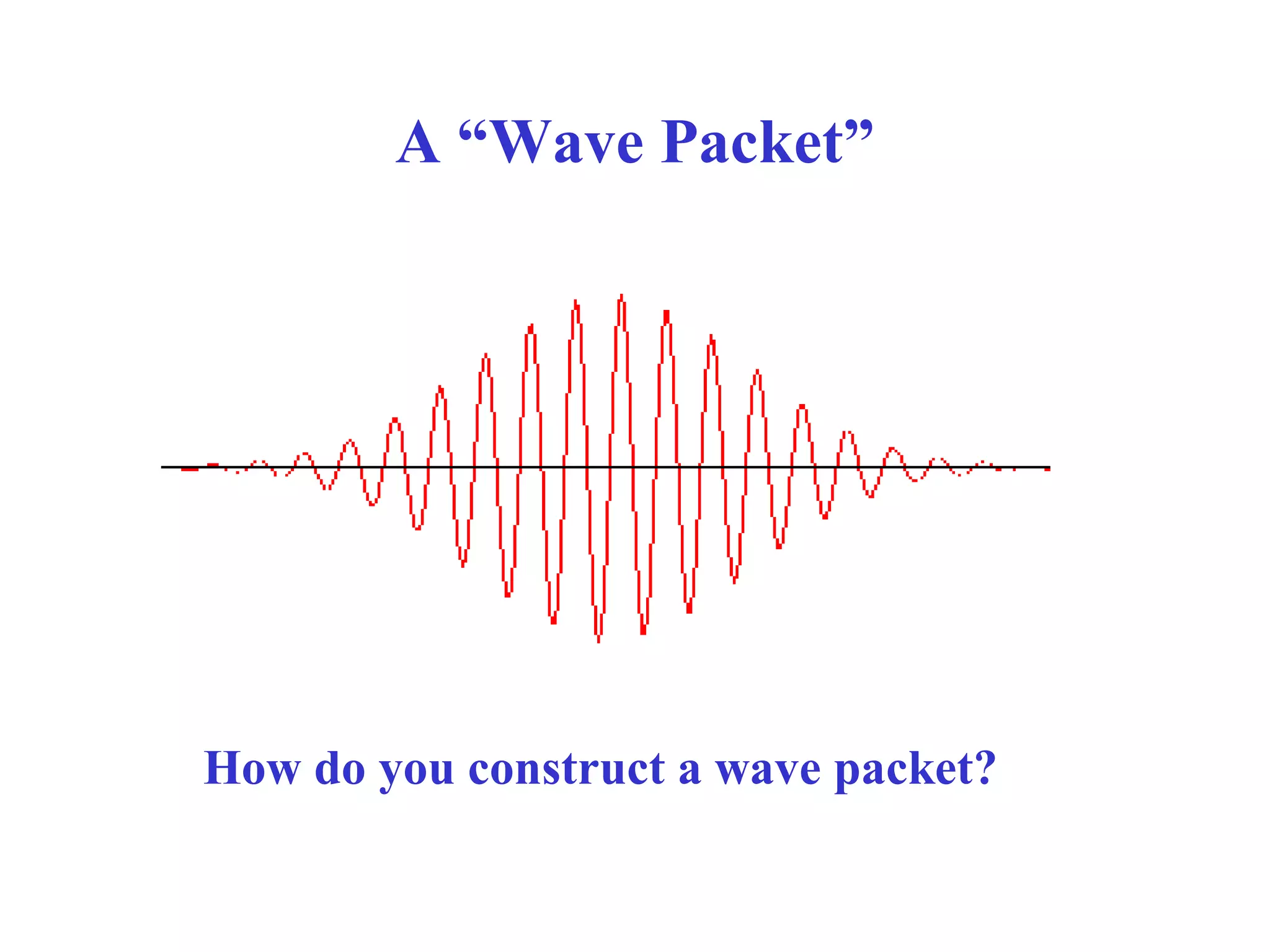
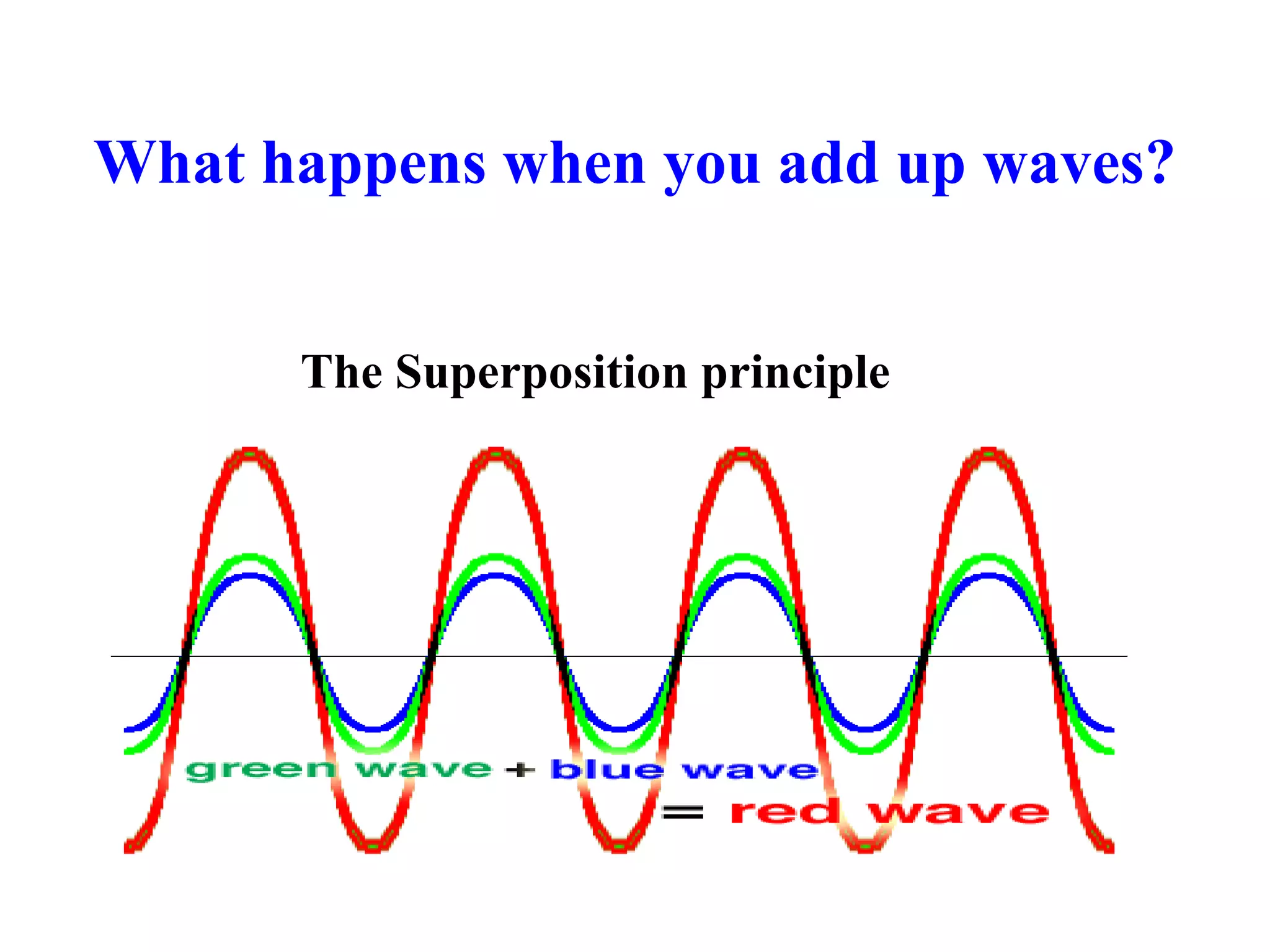
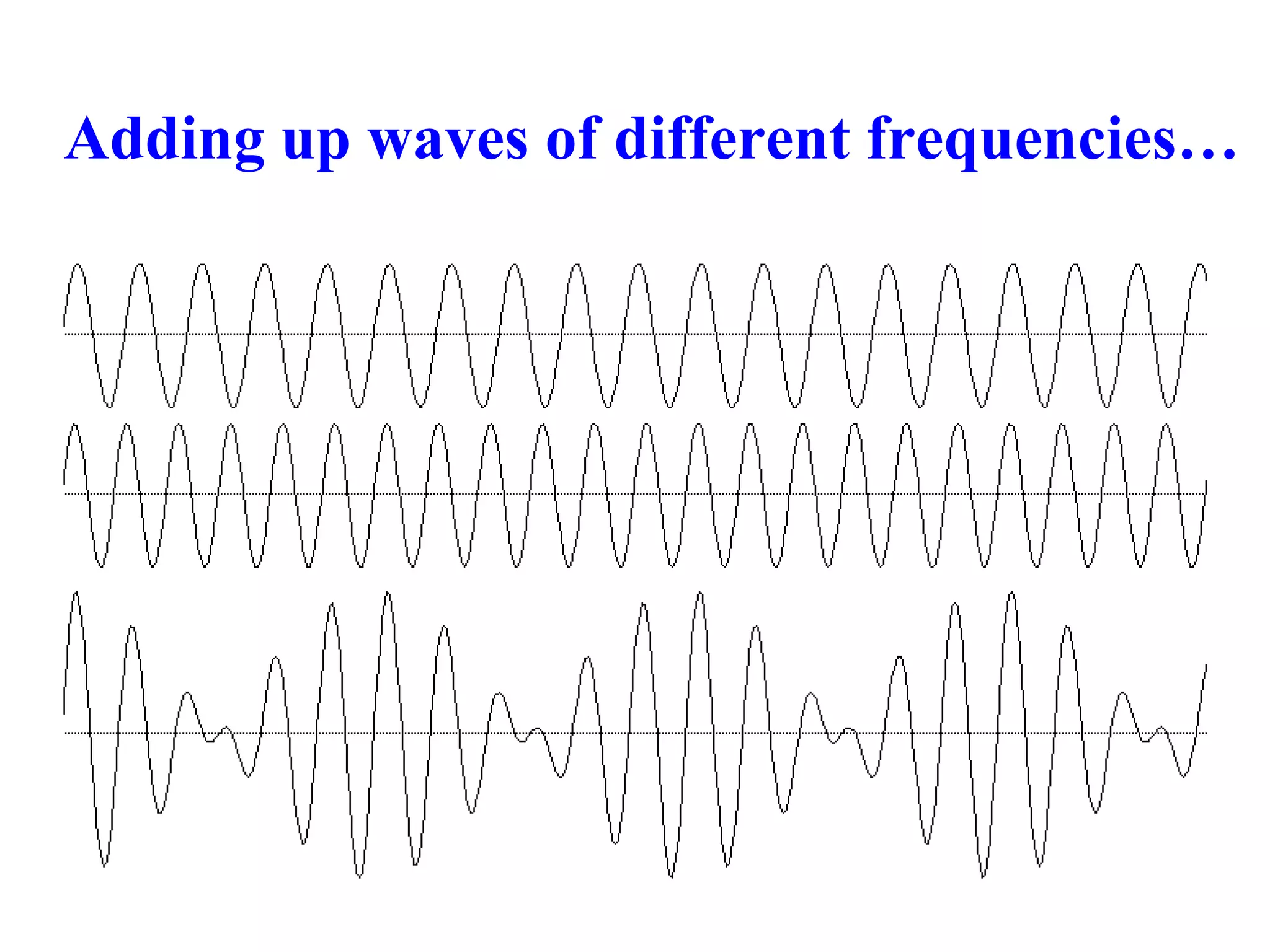
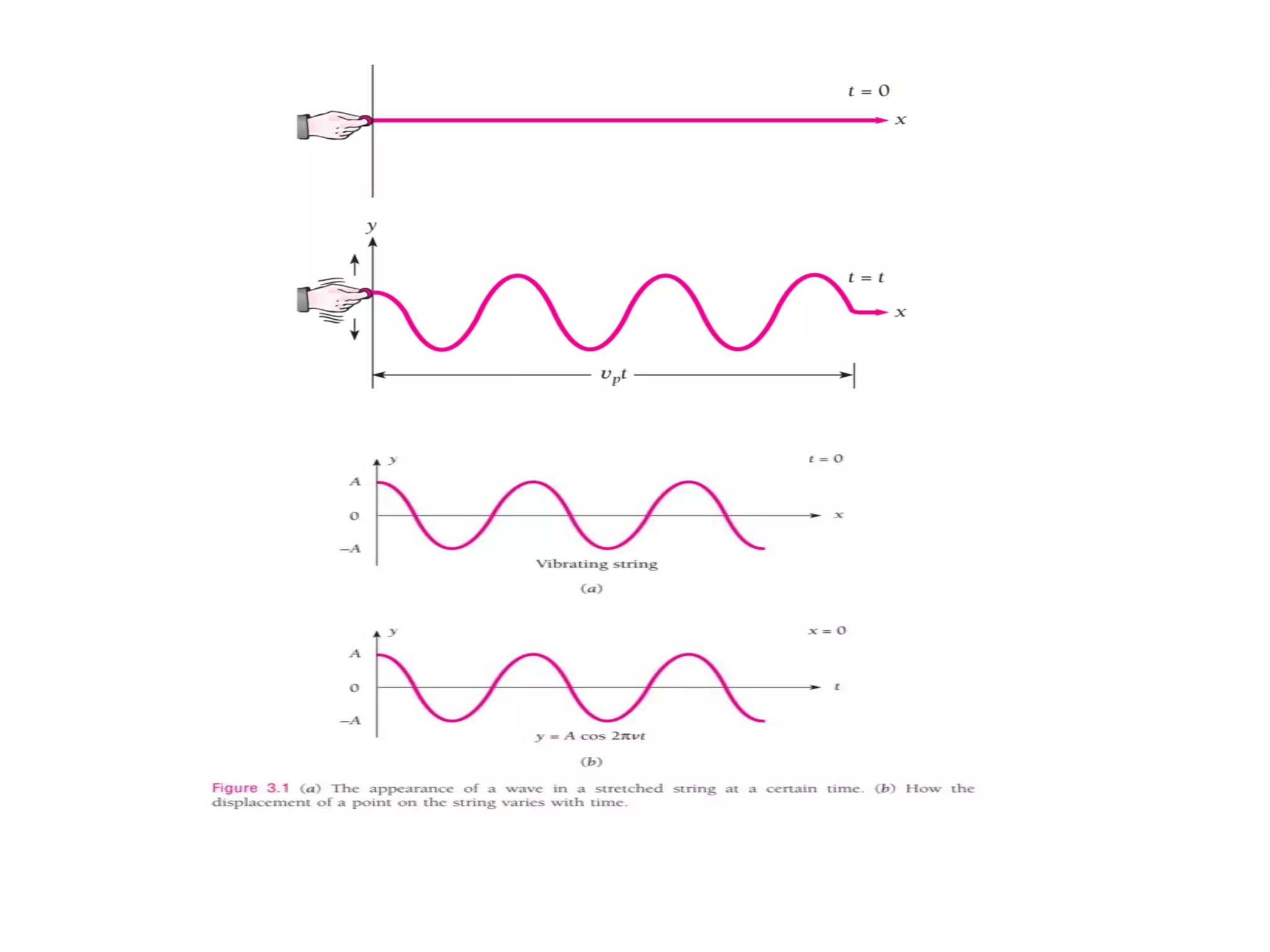
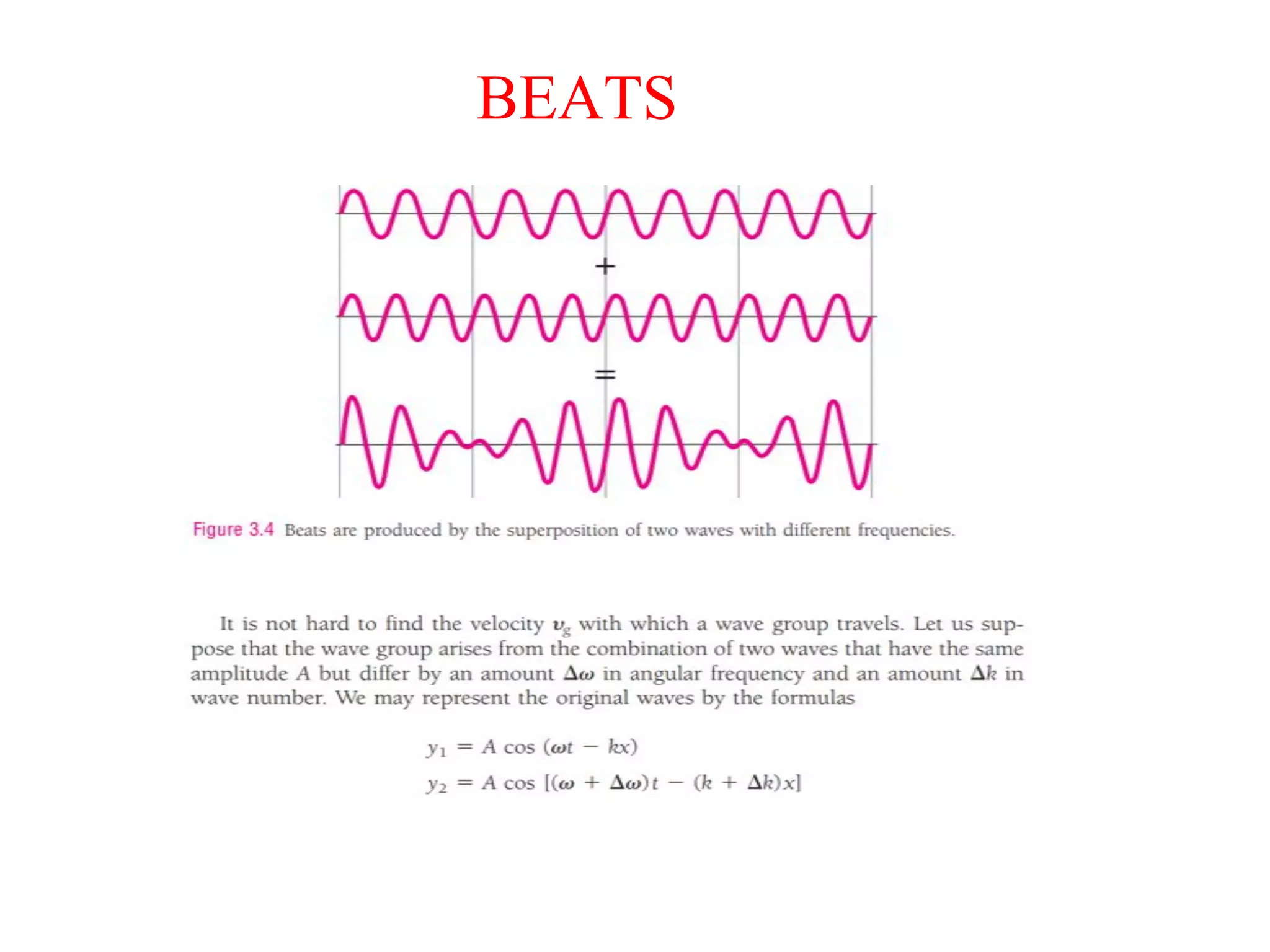
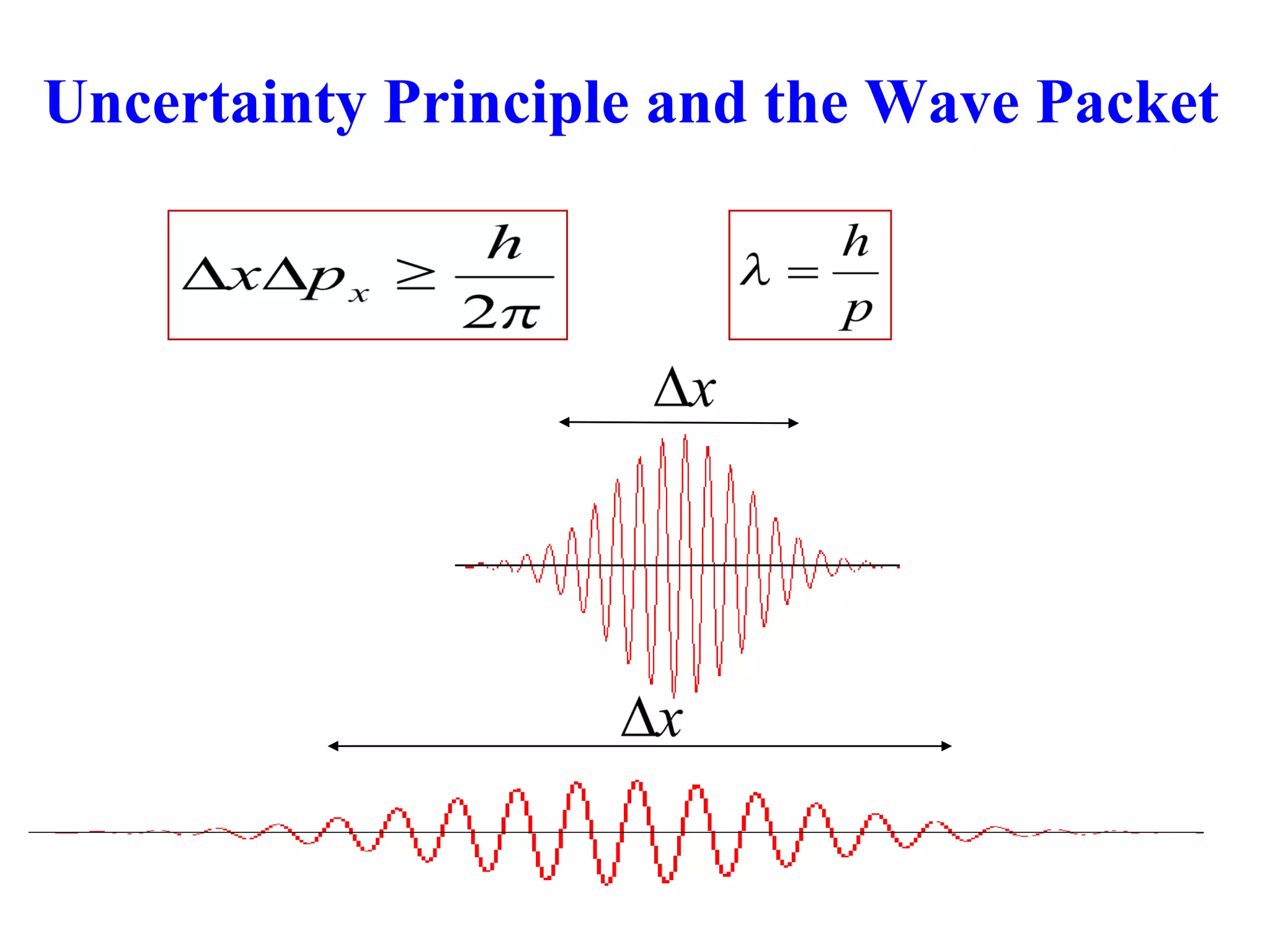
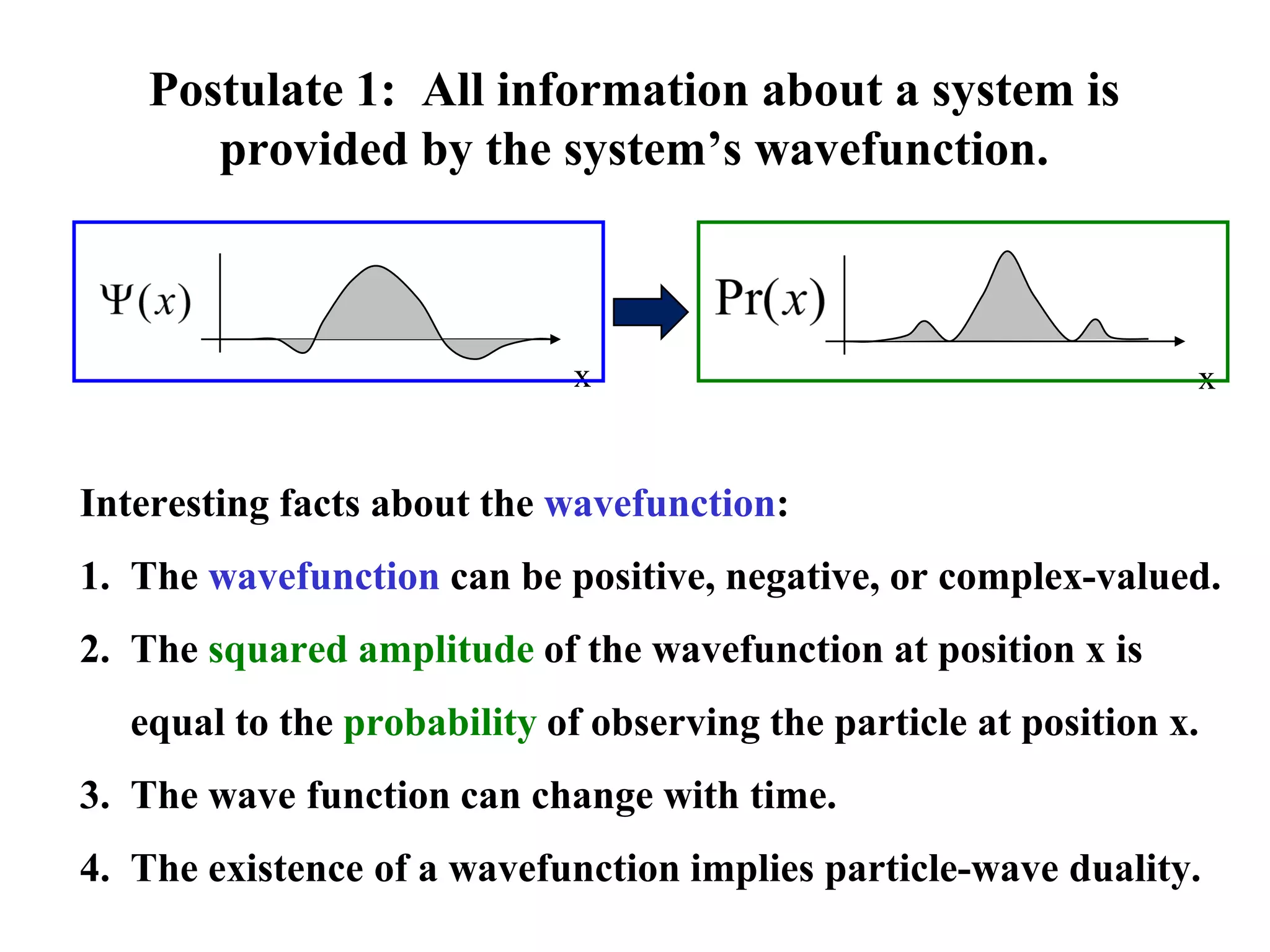
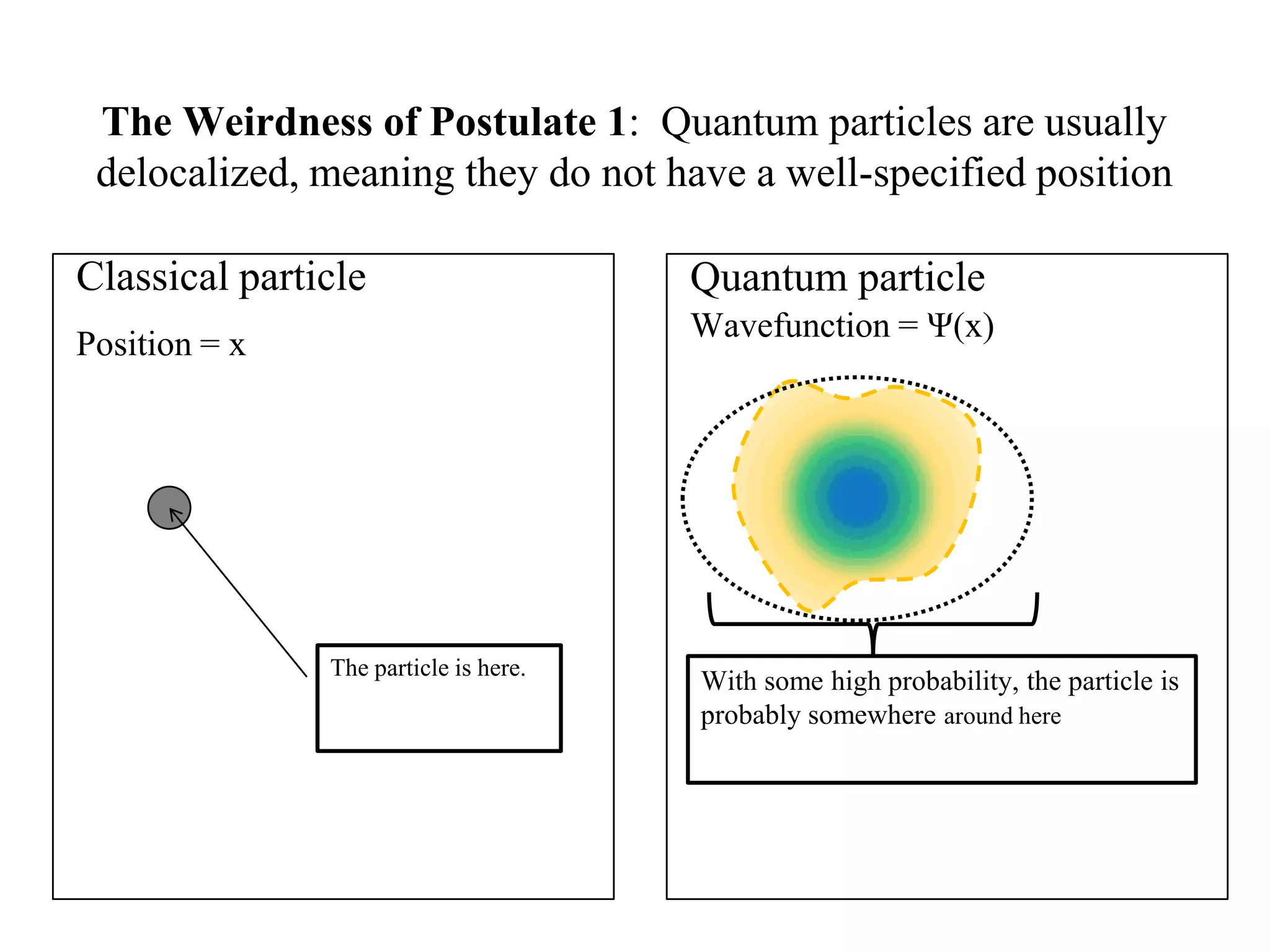
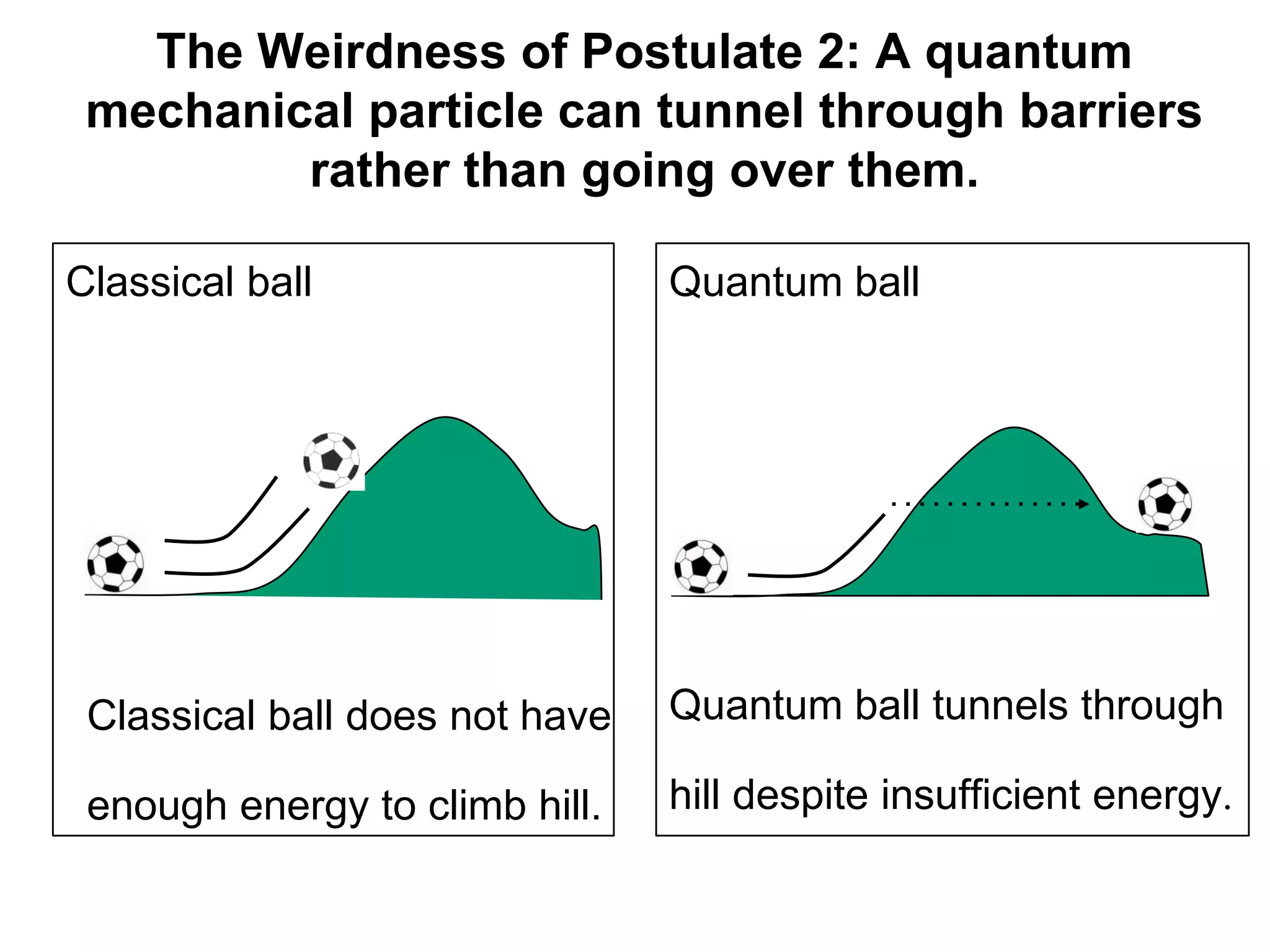
The document discusses the development of quantum mechanics and wave-particle duality, including de Broglie's hypothesis that all matter has an associated wave nature. It covers key concepts like the wave function, wave packets, Heisenberg's uncertainty principle, and the Schrödinger equation governing the motion of quantum particles. Experimental evidence for matter waves is also discussed, showing that even large molecules can exhibit wave-like behavior.

1. Modern Physics
Dr.N.Meenakshisundaram M.Sc., NET, Ph.D. (IITM)
Assistant Professor of Physics
Vivekananda College
Madurai - 625234

2. The Birth of Quantum Mechanics
Wave – Particle Duality

3. Wave Properties of Particles
● de-Broglie Waves
● Waves of Probability
● Describing a Wave
● Phase and Group Velocity
● Davisson and Germer Experiment
● Particle in a Box
● Uncertainty Principle and Its Applications

4. If light, which was traditionally understood as a
wave also turns out to have a particle nature,
might matter, which is traditionally understood as
particles, also have a wave nature?
Yes!

5. Louis de Broglie’s hypothesis
The dual nature of matter
A particle with momentum p has a matter wave
associated with it, whose wavelength is given by

6. Why isn’t the wave nature of matter
more apparent to us…?
Planck’s constant is so small that we don’t observe
the wave behaviour of ordinary objects – their de
Broglie wavelengths could be many orders of
magnitude smaller than the size of a nucleus!

7. Some Typical de Broglie wavelengths
A human being weighing 70 kg, and moving with a
speed of 25 m/s ~ 3.79 x 10-37 meters.
A ball weighing 100 g, and moving with a speed of
25 m/s ~ 2.65 x 10-34 meters.
An electron accelerated through a potential
difference of 50 V ~ 1.73 x 10-10 meters.

8. Particle
Our traditional understanding of a particle…
“Localized” - definite position, momentum, confined
in space

9. Wave
Our traditional understanding of a wave….
“de-localized” – spread out in space and time

10. How do we associate a wave nature to a
particle?
What could represent both wave and particle?
• Find a description of a particle which is consistent
with our notion of both particles and waves……
• Fits the “wave” description
• “Localized” in space

11. A “Wave Packet”
How do you construct a wave packet?

12. What happens when you add up waves?
The Superposition principle

13. Adding up waves of different frequencies…

14. Constructing a wave packet by adding
up several waves …
If several waves of different wavelengths
(frequencies) and phases are superposed together,
one would get a resultant which is a localized wave
packet

15. A wave packet describes a particle
• A wave packet is a group of waves with slightly
different wavelengths interfering with one another
in a way that the amplitude of the group (envelope)
is non-zero only in the neighbourhood of the
particle
• A wave packet is localized – a good representation
for a particle!

16. Waves of Probability
1. The quantity whose variations make up matter
waves is called the wave function, symbol Ѱ
2. The value of the wave function associated with a
moving body at the particular point x, y, z in space
at the time t is related to the likelihood of finding
the body there at the time.
Probability density:
“The probability of experimentally finding the body
described by the wave function Ѱ at the point x, y, z,
at the time t is proportional to the value of |Ѱ| 2 there
at t ”.

17. Describing a wave
A general formula for wave

22. BEATS

28. Wave Packet, Phase Velocity and Group
Velocity
• The velocities of the individual waves which
superpose to produce the wave packet representing
the particle are different - the wave packet as a
whole has a different velocity from the waves that
comprise it
• Phase Velocity: The rate at which the phase of the
wave propagates in space
• Group Velocity: The rate at which the envelope of
the wave packet propagates

29. Wave Packet, Phase Velocity and Group
Velocity
• The spread of wave packet in wavelength depends
on the required degree of localization in space –
the central wavelength is given by
• What is the velocity of the wave packet?

30. Wave Packet, Phase Velocity and Group
Velocity
Phase velocity
Group velocity
Here is the velocity of light and is the
velocity of the particle

31. Particle in a Box

34. Heisenberg's Uncertainty Principle
• The Uncertainty Principle is an important
consequence of the wave-particle duality of matter
and radiation and is inherent to the quantum
description of nature
• Simply stated, it is impossible to know both the
exact position and the exact momentum of an object
simultaneously
A fact of Nature!

35. Heisenberg's Uncertainty Principle
Uncertainty in Position :
Uncertainty in Momentum :

36. Heisenberg's Uncertainty Principle
- applies to all “conjugate variables”
Position & Momentum
Energy & Time

37. Uncertainty Principle and the Wave Packet
If is large, is small

38. Some consequences of the Uncertainty
Principle
• The path of a particle (trajectory) is not well-defined
in quantum mechanics
• Electrons cannot exist inside a nucleus
• Atomic oscillators possess a certain amount of energy
known as the zero-point energy, even at absolute zero

39. Why isn’t the uncertainty principle
apparent to us in our ordinary
experience…?
Planck’s constant, again!!
Planck’s constant is so small that the uncertainties
implied by the principle are also too small to be
observed. They are only significant in the domain of
microscopic systems

40. Are Matter Waves for Real?!
• In 1927 Davisson and Germer showed that
electrons can diffract – they act like waves
• Big application – Electron Microscopes

41. Are matter waves for real?!
__________________________________
Double –slit experiment with electrons (1989)
(www.hqrd.hitachi.co.jp/em/doubleslit.cfm)

42. Are matter waves for real?!
• Today, advances in technology have led to matter
wave interference experiments being
demonstrated successfully not only with electrons
but neutrons, atoms, and big and small molecules!
• In fact, the largest molecule showing interference
has almost a 100 atoms!

43. Are matter waves for real?!
__________________________________
• C60 molecules (Fullerenes or Bucky Balls) have a wave
nature! (A. Zeilinger et al, Vienna, 1999)
• Biomolecules have it too!
Porphyrin (2003)

44. True understanding of nature required that physical objects,
whatever they are, are neither exclusively particles or waves. No
experiment can ever measure both aspects at the same time, so
we never see a mixture of particle and wave.
When one observes a physical phenomenon involving a physical
object, the behaviour you will observe – whether particle like or
wave like – depends on your method of observation. The object
is described by mathematical functions which are measures of
probability.

45. Matter waves are real….
If there is wave, there must be a wave equation………
The Schrödinger Equation

46. The Fundamental Postulates of
Quantum Mechanics
Postulate 1: All information about a system is
provided by the system’s wave function.
Postulate 2: The motion of a nonrelativistic
particle is governed by the Schrodinger equation
Postulate 3: Measurement of a system is associated
with a linear, Hermitian operator

47. Postulate 1: All information about a system is
provided by the system’s wavefunction.
x x
Interesting facts about the wavefunction:
1. The wavefunction can be positive, negative, or complex-valued.
2. The squared amplitude of the wavefunction at position x is
equal to the probability of observing the particle at position x.
3. The wave function can change with time.
4. The existence of a wavefunction implies particle-wave duality.

48. The Weirdness of Postulate 1: Quantum particles are usually
delocalized, meaning they do not have a well-specified position
Classical particle Quantum particle
The particle is here.
With some high probability, the particle is
probably somewhere around here
Position = x
Wavefunction = Ψ(x)

49. Postulate 2: The motion of a nonrelativistic particle is
governed by the Schrödinger equation
Interesting facts about the Schrödinger Equation:
1. It is a wave equation whose solutions display interference effects.
2. It implies that time evolution is unitary and therefore reversible.
3. It is very, very difficult to solve for large systems (i.e. more
than three particles).
Time-dependent S.E.:
Time-independent S.E.:
Molecular S.E.:

50. The Weirdness of Postulate 2: A quantum
mechanical particle can tunnel through barriers
rather than going over them.
Classical ball Quantum ball
Classical ball does not have
enough energy to climb hill.
Quantum ball tunnels through
hill despite insufficient energy.

51. The wavefunction is the solution to the
Schrödinger wave equation:
We’re not going to go into the details of the derivation or the
solution of the Schrödinger equation. However, it is essential to
realise that the equation above has much in common with (but
also some important differences to) the classical wave equation :
(In one dimension)
The Schrödinger wave equation

52. Reference Text Book
Concepts of Modern Physics - Arthur Beiser,
Sixth Edition 2004, Tata McGraw-Hill Publishing
Company Limited, New Delhi
Chapter 3 : 3.1 - 3.9
Acknowledgement
References collected from Google Search!!