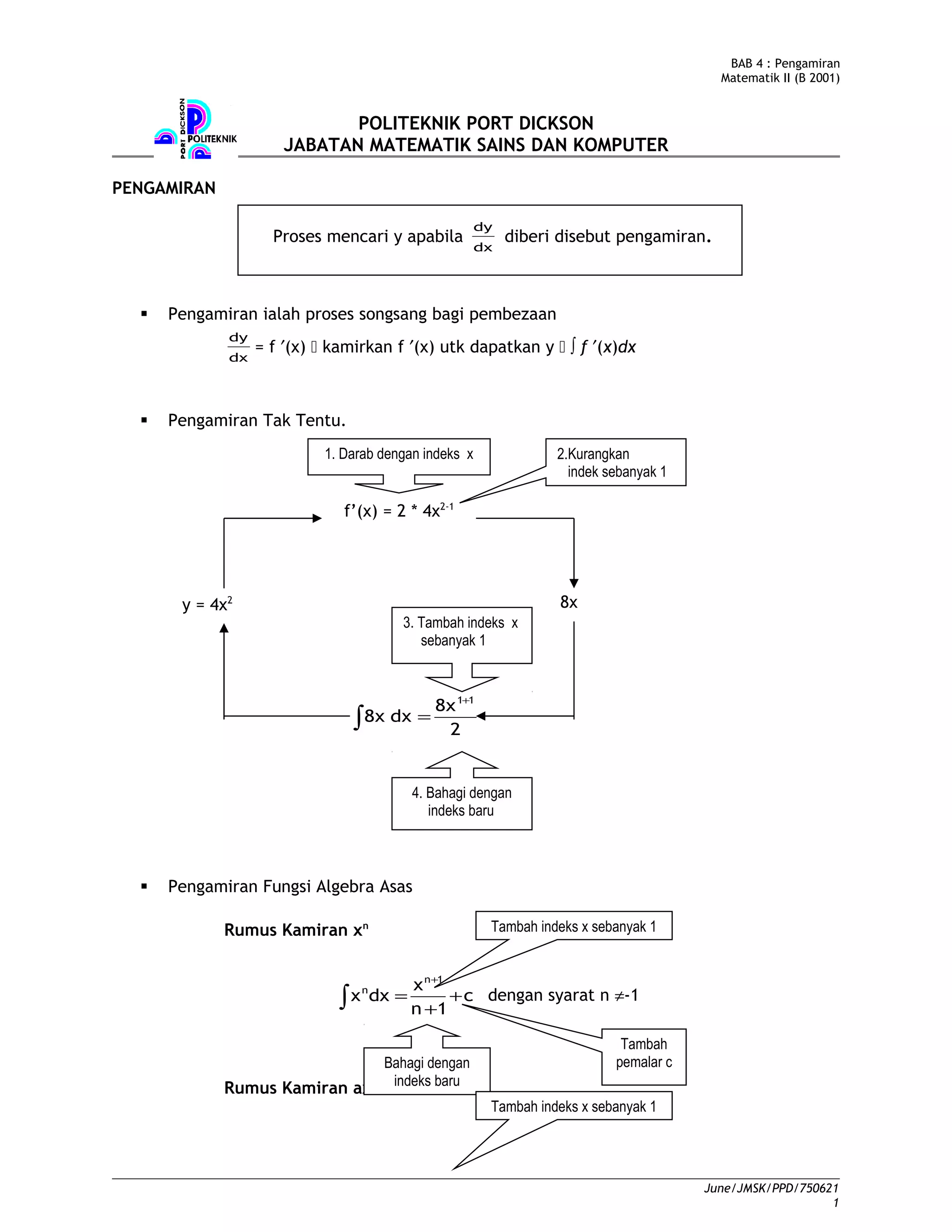
Dokumen ini membincangkan konsep pengamiran dalam matematik, termasuk rumus-rumus pengamiran fungsi algebra, logarithma, trigonometri, dan eksponen. Ia menerangkan kaedah pengamiran tak tentu, hasil tambah, hasil tolak, serta penggantian, disertai dengan contoh-contoh dan langkah-langkah penyelesaian. Terdapat juga latihan untuk menguji pemahaman tentang topik pengamiran.

1. BAB 4 : Pengamiran
Matematik II (B 2001)
POLITEKNIK PORT DICKSON
JABATAN MATEMATIK SAINS DAN KOMPUTER
PENGAMIRAN
Proses mencari y apabila
dx
dy
diberi disebut pengamiran.
 Pengamiran ialah proses songsang bagi pembezaan
dx
dy
= f ′(x)  kamirkan f ′(x) utk dapatkan y  ∫ f ′(x)dx
 Pengamiran Tak Tentu.
 Pengamiran Fungsi Algebra Asas
Rumus Kamiran xn
c
1n
x
dxx
1n
n
+
+
=
+
∫ dengan syarat n ≠-1
Rumus Kamiran axn
June/JMSK/PPD/750621
1
f’(x) = 2 * 4x2-1
∫
+
=
2
8x
dx8x
11
y = 4x2 8x
4. Bahagi dengan
indeks baru
1. Darab dengan indeks x 2.Kurangkan
indek sebanyak 1
3. Tambah indeks x
sebanyak 1
Tambah indeks x sebanyak 1
Bahagi dengan
indeks baru
Tambah
pemalar c
Tambah indeks x sebanyak 1

2. BAB 4 : Pengamiran
Matematik II (B 2001)
c
1n
ax
dxax
1n
n
+
+
=
+
∫ dengan syarat n ≠-1
 Contoh Soalan
1. c2xc
2
4x
dx4x 2
2
+=+=∫
4. ∫ +−=− c23ydy23
2. c
8
7x
c
4
x
2
7
dx
2
7x 443
+=+×=∫
5. ∫ += c10zdz10
3. c
6
t
dtt
6
5
+=∫ 6. ∫ dk5k = c
2
5k2
+
 Pengamiran Hasil Tambah & Hasil Tolak
Fungsi lebih drpd byk fungsi lain, kamirkan setiap fungsi satu demi satu.
a) Pengamiran hasil tambah  ∫ ∫ ∫+=+ q(x)dxp(x)dxq(x)]dx[p(x)
b) pengamiran hasil tolak  ∫ ∫ ∫−=− q(x)dxp(x)dxq(x)]dx[p(x)
Contoh:
a. ∫ ∫ ∫+=+ dx3dx2x3]dx[2x
= c3x
3
2x3
++
b. dt
3
2t
dt3tdt]
3
2t
[3t 55
∫ ∫∫ −=−
= c
23
2t
6
3t 26
+
×
−
= c
3
t
2
t 26
+−
c. ∫ ∫ −−=+− dx2]x[6xdx1)2)(2x(3x 2
= ∫ dx6x2
∫− x dx2∫−
= c2x
2
x
3
6x 23
+−−
June/JMSK/PPD/750621
2
Tambah satu
pemalar sahaja
Kembangkan utk mendapat
Bahagi dengan
indeks baru
Tambah
pemalar c
Tambah satu
pemalar sahaja

3. BAB 4 : Pengamiran
Matematik II (B 2001)
= c2x
2
x
2x
2
3
+−−
d. dx]
x
2x
x
4x
[dx
x
2x4x 5353
−=
−
∫∫
∫ ∫−= dx2xdx4x 42
c
5
2x
3
4x 53
+−=
 Pengamiran Melalui Penggantian
Cari, ∫ − dx3)(2x 5
Penyelesaian : anggap u = 2x – 3.
Maka, 2
dx
du
= ⇒
2
du
dx =






=− ∫∫ 2
du
udx3)(2x 55
duu
2
1 5
∫=
c
15
u
2
1 15
+
+
×=
+
c
62
3)(2x 6
+
×
−
=
c
12
3)(2x 6
+
−
=
Contoh :
a. Cari kamiran bagi ∫ + dx5)(3x 6
Anggap : u = 3x + 5
3
dx
du
= ⇒
3
du
dx =
∫ ∫=+
3
du
udx5)(3x 66
June/JMSK/PPD/750621
3
Bahagikan setiap sebutan
pengangka dengan x
Gantikan (2x-3)
dengan u
Gantikan dx dengan
Ganti semula
u = (2x-3)
Gantikan
(3x+5) dengan
u
Gantikan dx dengan

4. BAB 4 : Pengamiran
Matematik II (B 2001)
c
7
u
3
1 7
+





=
c
21
5)(3x 7
+
+
=
 Rumus-Rumus Melalui Kaedah Penggantian
Rumus Kamiran (ax+ b) n
( ) ( )
( )∫ +
+
+
=+
+
c
1na
bax
dxbax
1n
n
, 1n −≠
a. c
22
1)(2x
dx1)(2x
2
+
×
+
=+∫ b. c
33
4)(3x
dx4)(3x
3
2
+
×
−
=−∫
c
4
1)(2x 2
+
+
= c
9
4)(3x 3
+
−
=
c.
c
20
7)(4t
c
54
7)(4t
dt7)(4t
5
5
4
+
+
=
+
×
+
=+∫
d.
c
3
1)(3k
c
1)(3
1)(3k
dk1)(3k
1
1
2
+
−
−=
+
−×
−
=−
−
−
−
∫
 PENGAMIRAN FUNGSI LOGARITHMA, TRIGONOMETRI & EKSPONEN
 Kamiran Fungsi Salingan x,
x
1
;
utk semua nilai x 
 cxlndx
x
1
+=∫

( )
cbaxln
a
1
dx
bax
1
++=
+∫
June/JMSK/PPD/750621
4
Gantikan semula
u dengan 3x + 5
Tambah indeks n
sebanyak 1
Bahagi dengan indeks baru
didarab dengan pekali x
Tambah
pemalar c
Semua nilai
mesti +ve

5. BAB 4 : Pengamiran
Matematik II (B 2001)

( )
( )
( )∫∫ =
+
dx
xf
xf'
dx
bax
1
n
 Contoh
a)
cxln
2
1
dx
x
1
2
1
dx
2x
1
+=
=∫ ∫
b)
cx3ln
dx
x
1
3dx
x
3
+−=
−=
−
∫ ∫
c)
cxln
5
1
dx
x
1
5
1
dx
5x
1
+−=
−=−∫ ∫
d)
∫ ++=
+
c32tln
2
1
dt
32t
1
e)
∫ +−= c2x-5ln
2
1
dx
2x-5
1 f)
∫ ++=
+
c25xln
5
1
dx
25x
1
g)
∫ +
dx
3x
x
2
katakan ( ) 3xxf 2
+=
( ) 2xxf' =
maka
c3xln
2
1
dx
3x
2x
2
1
dx
3x
x
2
22
++=
+
=
+∫ ∫
h)
∫ +
dp
3p
p
5
4
katakan ( ) 3pxf 5
+=
( ) 4
5pxf' =
maka
c3pln
5
1
dp
3p
5p
5
1
dp
3p
p
5
5
4
5
4
++=
+
=
+ ∫∫
 Kamiran Fungsi Trigonometri
1. cxkosdxxsin +−=∫
2. cxsindxxkos +=∫
3. cxtandxxsek2
+=∫
4. caxkos
a
dxaxsin +−=∫
1
5. caxsin
a
dxaxkos +=∫
1
6. caxtan
a
dxaxsek2
+=∫
1
June/JMSK/PPD/750621
5
Tulis semula
dalam
bentuk
Tulis semula
dalam
bentuk

6. BAB 4 : Pengamiran
Matematik II (B 2001)
7. cb)(axkos
a
dxb)(axsin ++−=+∫
1
8. cb)(axsin
a
dxb)(axkos ++=+∫
1
9. cb)(axtan
a
dxb)(axsek2
++=+∫
1
 Contoh:
a)
cxsin3
dxxkos3dxxkos3
+−=
−=−∫ ∫
b)
cxtan
2
1
dxxsek
2
1
dx
2
xsek 2
2
+=
=∫
c)
c4xsin
2
1
c4xsin
4
1
2
dx4xkos2dx4xkos2
+=
+•=
=∫ ∫
d)
cx
3
1
sin3
cx
3
1
sin
3
1
1
xdx
3
1
kosdx
3
x
kos
+=
+=
=∫∫
e)
c1)(3kkos
6
1
c1)(3kkos
3
1
2
1
dk1)(3ksin
2
1
dk1)(3ksin
2
1
++−=
++−•=
+=+∫ ∫
f)
c3x)-(1tan
3
5
c3x)-(1tan
3
1
5
dx3x)-(1sek5dx3x)-(1sek5 22
+−=
+−•=
=∫ ∫
g)
dx
xkos
xsin
dxxtan ∫∫ =
katakan ( ) xkosxf =
( ) xsinxf' −=
maka
June/JMSK/PPD/750621
6
Tulis semula
dalam
bentuk

7. BAB 4 : Pengamiran
Matematik II (B 2001)
cxkosln
dx
xkos
xsin-
dx
xkos
xsin
+−=
=∫∫
h)
dx
xsin
xkos
dxxkot ∫∫ =
katakan ( ) xsinxf =
( ) xkosxf' =
maka
cxsinln
dx
xsin
xkos
dx
xsin
xkos
+=
=∫∫
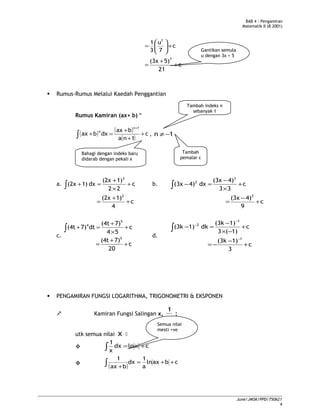
 Pengamiran Melalui Penggantian – Identiti Trigonometri
 Jika soalan trigo yang mempunyai kuasa maka penyelesaian masalah mesti
menggunakan identiti trigo.
 Langkah-langkah penyelesaian masalah
1. Tukar ke bentuk yg boleh dikamirkar dgn menggunakan identiti trigo. –
pilih identiti trigo yg sesuai
2. salin balik soalan yg telah ditukat bentuk dan selesaikan.
a) ∫ dx3xkos2
[ ]
cx
2
1
6xsin
12
1
cx6xsin
6
1
2
1
dx1dx6xkos
2
1
1)dx6x(kos
2
1
++=
+



+=
+=
+=
∫ ∫
∫
Diketahui : 1A2kos2Akos 2
−=
Gantikan : 3xA =
1)6x(kos
2
1
2
12(3x)kos
3xkos
12(3x)kos3x2kos
13x2kos2(3x)kos
2
2
2
+=
+
=
+=
−=
b) ∫ dx3xtan2
cx3xtan
3
1
dx1dx3xsek
dx1)3x(sek
2
2
+−=
−=
−=
∫ ∫
∫
Diketahui : Atan1Asek 22
+=
Gantikan : 3xA =
1-3xsek3xtan
3xtan13xsek
22
22
=
+=
c)
∫ dx
3
x
sin2 Diketahui : Asin12Akos 2
2−=
2A)kos(1
2
1
2
2Akos1
Asin
2Akos1Asin2
2
2
−=
−
=
−=
June/JMSK/PPD/750621
7
1
2
Tulis semula
dalam
bentuk
2
1

8. BAB 4 : Pengamiran
Matematik II (B 2001)
cx
3
2
sin
4
3
x
2
1
cx
3
2
sin
2
3
x
2
1
cx
3
2
sin
3
2
1
x
2
1
dxx
3
2
kosdx1
2
1
x)dx
3
2
kos(1
2
1
x)dx
3
2
kos(1
2
1
+−=
+





−=
+








−=




−=
−=
−=
∫∫
∫
∫ Gantikan :
3
x
A =
x)
3
2
kos(1
2
1
3
x
sin2
−=
 Kamiran Fungsi Eksponen
1. ∫ += cedxe xx
2. ∫ += ce
a
1
dxe axax
3. ∫ += ++
ce
a
1
dxe baxbax
 Contoh:
a) ∫ += cedxe xx
b)
∫ +
−
= −−
ce
4
1
dxe 4x4x
c)
c2e
ce
2
1
1
dxe
x
2
1
x
2
1
x
2
1
+−=
+
−
=
−
−−
∫
d)
ce
3
1
dxe 53x53x
+= ++
∫
Soalan Latihan
1. Cari setiap kamiran berikut.
a. ∫ + dxxx ]4[ 23
= cx
x
++ 3
4
3
4
4
b. dt
t
t ]
1
3[ 3
3
−∫ = c
t
t ++ 2
4
2
1
4
3
c. dx
x
]3
2
[ 2
−∫ = cx
x
+−− 3
2
2. Nilaikan yang berikut:
June/JMSK/PPD/750621
8

9. BAB 4 : Pengamiran
Matematik II (B 2001)
a. ∫ +− dkkk ]44[ 2
= ckk
k
++− 42
3
2
3
b. ∫ − dzz 2
)32( = czzz ++− 96
3
4 23
c. dx
x
x
∫
+
2
5
42
= cx
x
++− 42
3. Nilaikan kamiran yang berikut:
a. ∫ dz7 = 7z +c
b. ∫ dtt3
2 = c
t
+
5
2 5
c. dx
x∫ 4
10
= c
x
+− 3
3
10
d. ( )∫ −+ dxxxx 96 2
= cxxx +−+ 323
3
2
2
9
2
e. ( )∫ − dzx
2
52 = cxx
x
++− 2510
3
4 2
3
4. Tuliskan semula ungkapan berikut supaya ia boleh diselesaikan dengan
menggunakan rumus hasil tambah dan hasil tolak pengamiran.
a. (3x - 2)2
= cxxx ++− 463 23
b. 5
2
)1(
x
xx −
= c
xx
+−
1
2
1
2
c. 2
)1)(1(
k
kk −+
= c
k
k ++
1
5. Selesaikan:
a. ∫ + dss3
34 = css ++ 4
4
3
4
b. ∫ − dzx 2
)76( = cxxx ++− 32
3
49
2136
Soalan Latihan
1. Dapatkan setiap kamiran berikut:
a. dxx∫ − 4
)32( = c
x
+
−
10
)32( 5
b. dzz∫ + 3
)63( = c
z
+
+
12
)63( 4
c. ∫ − dtt 5
)75( = c
t
+
−
−
42
)75( 6
d. dxx∫ + 3
)84(6 = c
x
+
+
8
)84(3 4
e. ∫
−
− dxx 3
)27( = c
x
+
−
− 2
)27(14
1
f. dt
t∫ + 2
)31(
π
= c
t
+
+
−
)31(3
π
June/JMSK/PPD/750621
9

10. )()()]([)( aFbFxFxf b
a
b
a
−==∫
BAB 4 : Pengamiran
Matematik II (B 2001)
g. dx
x∫ − 3
)54(
1
= c
x
+
−
− 2
)54(8
1
h. dx
x∫ +
−
4
)53(2
3
=
c
x
+
+ 3
)53(6
1
a. Nilaikan kamiran berikut:
a. dkkk∫ − 732
)1( = ( ) ck +−
− 83
1
24
1
b. dzzzz∫ −− )33()3( 233
= ( ) css +−
32
3
3
1
c. dp
pp
p
∫ +
+
3 3
2
3
1
= ( ) cpp ++ 3
2
3
3
2
1
PENGAMIRAN TENTU
CONTOH
a. 2
0
2
2
0
]x
2
x
[dx)1(x +=+∫
4
0)(02)
2
2
(
2
=
+−+=
June/JMSK/PPD/750621
10
Hasil pengamiran Gantikan x = b
a disebut had bawah
pengamiran dan b
had atas pengamiran
Gantikan x = a
Gantikan semua x dengan 2
Gantikan semua x dengan 0

11. BAB 4 : Pengamiran
Matematik II (B 2001)
b.
2
1
23
2
1
2
2
3x
3
2x
dx3x)(2x 





−=−∫
6
1
2
3
3
2
6
3
16
2
13
3
12
2
23
3
22 2323
=






−−





−=





 ×
−
×
−




 ×
−
×
=
c.
2
1
3
2
2
1
2
3
x
2xdx)x(4x
−
− 





−=−∫
3
3
1
2
3
8
8
3
1)(
1)(2
3
2
22
3
2
3
2
=






+−





−=





 −
−−×−





−×=
SOALAN LATIHAN
a) ∫ −
3
2
2
dx5x)(x
( ) ( )
6
37
atau
6
1
6
3
22
2
27
2
20
3
8
2
45
3
27
2
25
3
2
2
35
3
3
2
5x
3
x
dx5x)(x
2323
3
2
23
3
2
2
−−=






−−−=




−−



−=








−−







−=






−=−∫
b) dx
x
5xx1
2 3
4
∫
−
−
+
June/JMSK/PPD/750621
11

12. BAB 4 : Pengamiran
Matematik II (B 2001)
1
2
9
2
11
2
5
25
2
1
2)(
5
2
2)(
1)(
5
2
1)(
x
5
2
x
dx)5x(xdx
x
5xx
22
1
2
2
1
2
2
1
2 3
4
=
−=






+−





+=






−
−
−
−





−
−
−
=






−=
+=
+
−
−
−
−
−
−
− ∫∫
c) ∫ +−
4
2
dt2t)3t)(1(1
116
2(2)
2
2
22(4)
2
4
4
2t
2
t
t
dt)6tt1(dt2t)3t)(1(1
3
2
3
2
4
2
3
2
4
2
2
4
2
−=






−−−





−−=






−−=
−−=+− ∫∫
d) ∫ −
3
0
dx3)
3
2x
(
69
6
18
3(0)
6
2(0)
3(3)
6
2(3)
3x
23
2x
dx3)
3
2x
(
22
3
0
2
3
0
−=−=






−−





−=






−
×
=−∫
e) ( )∫ −+
3
1
2
dx16x2x
June/JMSK/PPD/750621
12

13. BAB 4 : Pengamiran
Matematik II (B 2001)
( )
( ) ( ) ( ) ( )
[ ]
3
1
39atau
3
118
3
8
42
13
3
2
32718
1131
3
2
3333
3
2
x3x
3
2x
x
2
6x
3
2x
dx16x2x
2323
3
1
2
3
3
1
23
3
1
2
=
−=




−+−−+=




−+−



−+=






−+=






−+=−+∫
f) Satu objek dicampakkan ke bawah daripada sebuah helikopter pada masa sifar (t=0).
Objek itu mempunyai halaju v=13 +10t meter per saat. Jika objek itu mencecah tanah
selepas 10 saat, apakah jarak helikopter daripada tanah pada masa t = 10 saat?
[ ]
630
05(10)13(10)
5
10t
13t
)dt10t13(
2
10
0
2
10
0
=
−+=






+=
+= ∫
KAMIRAN TENTU BAGI FUNGSI SELANJAR DALAM SELANG TERTUTUP [a, b]
Contoh:
Diberi 6dxf(x)
5
3
=∫ , nilaikan kamiran berikut.
a)
∫
5
3
dx3f(x)
18
63
dxf(x)3
5
3
=
×=
= ∫
b)
( ) [ ]
( )
6
91512
3x62
dx3dxf(x)2
dx3)f(x)2(
5
3
5
3
5
3
5
3
=
−−=
−×=
−=
−
∫∫
∫
June/JMSK/PPD/750621
13
Ingat! dinilaikan
berasingan

14. ∫∫ −=
b
a
a
b
dxf(x)dxf(x)
∫∫∫ +=
c
b
b
a
c
a
dxf(x)f(x)dxf(x)
BAB 4 : Pengamiran
Matematik II (B 2001)
HAD KAMIRAN TENTU YANG DISALING TUKARKAN
CONTOH :
Diberi 12dxh(x)
5
1
=∫ , nilaikan kamiran berikut:
a) dxh(x)
1
5∫
12
dxh(x)
5
1
−=
−= ∫
b)
[ ]
72
25)(196
x12)8(
dx2xdxh(x)8
dx2x)(8h(x)
1
5
2
1
5
5
1
1
5
−
−−−=
−×−=
−−=
−
∫∫
∫
Kamiran Tentu Bagi Fungsi Hasil Tambah
CONTOH:
Diberi 5dxf(x)
6
2
=∫ , nilaikan kamiran berikut.
a)
∫
6
2
dx3f(x)
15
53
dxf(x)3
6
2
=
×=
= ∫
b)
[ ]
23
815
4)(1215
2x5)(3
dx2dxf(x)3
dx2)(3f(x)
6
2
6
2
6
2
6
2
=
+=
−+=
+×=
+=
+
∫∫
∫
June/JMSK/PPD/750621
14
Apabila had kamiran disaling tukarkan,
kamiran itu bertukar tanda.
Tukar tanda
Ingat!
dinilaikan
berasingan

15. BAB 4 : Pengamiran
Matematik II (B 2001)
CONTOH SOALAN
1. Jika
2
7
dxf(x)
1
2
=∫−
dan
2
3
dxf(x)
2
1
=∫ , nilaikan yang berikut.
a.
∫∫ +
−
2
1
1
2
dx2f(x)dxf(x)
2
1
6
2
13
2
3
2
2
7
dxf(x)2
2
7 2
1
=
=






+=
+= ∫
b.
∫−
2
2
dxf(x)
5
2
3
2
7
dxf(x)dxf(x)
2
1
1
2
=
+=
+= ∫∫−
c.
∫ ∫−
−
1
2
1
2
dxf(x)2dxf(x)
2
1
6atau
2
13
2
3
2
2
7
dxf(x)2
2
7 2
1
=
−×





−=
−×





−= ∫
2. Nilaikan yang berikut jika 1dxf(x)
3
2
−=∫ dan 4dxg(x)
3
1
=∫
a. dx)1(3f(x)
3
2∫ −
[ ]
4
13
2)(33
x1)3(
dx13f(x)dx
3
2
3
2
3
2
−=
−−=
−−−=
−−=
−=∫ ∫
b. )dxf(x)dxg(x)2(
3
2
3
1 ∫∫ −
10
28
1)2(2(4)
dxf(x)2dxg(x)2
3
2
3
1
=
+=
−−=
−= ∫∫
PENGAMIRAN TENTU MENGGUNAKAN KAEDAH GANTIAN
a.
( )∫ +
1
0
32
dx2xx
Andaikan
u = x2
+ 2
dx
du
= 2x
KESIMPULANNYA
1. Andaikan U
2. Bezakan U
3. dx jadikan tajuk
4. gantikan nilai x dalam u
5. kamirkan dan selesaikan
June/JMSK/PPD/750621
15

16. BAB 4 : Pengamiran
Matematik II (B 2001)
dx =
2x
du
Apabila x = 0 maka u = 0 + 2 = 2
Apabila x = 1 maka u = 1 + 2 = 3
Maka kamiran menjadi :
8
65
4
16
4
81
2
1
4
2
4
3
2
1
4
u
2
1
duu
2
1
2x
du
ux
44
3
2
4
3
2
3
3
2
3
=




−=






−=






=
=• ∫∫
b. dt
3t
3
6
1
∫ +
Andaikan
u = t + 3
dt
du
= 1
du = dt
Apabila t = 1 maka u = 1 + 3 = 4
Apabila t = 6 maka u = 6 + 3 = 9
Maka kamiran menjadi :
June/JMSK/PPD/750621
16
}

17. BAB 4 : Pengamiran
Matematik II (B 2001)
[ ]
6
2)6(3
496
2u3
2
1
u
3
duu3
dt
u
3
dt
3t
3
9
4
2
1
9
4
2
1
9
4
2
1
9
4
9
4
=
−=
−=






=










=
=
=
+
∫
∫∫
−
CONTOH SOALAN :
1. ( )∫ +
1
0
3
dx12x2
Andaikan
u = 2x + 1
dx
du
= 2
dx =
2
du
Apabila x = 0 maka u = 2(0) + 1 = 1
Apabila x = 1 maka u = 2(1) + 1 = 4
Maka kamiran menjadi :
20
4
1
4
81
4
1
4
3
4
u
duu
2
du
u2
44
3
1
4
3
1
3
3
1
3
=






−=






−=






=
=• ∫∫
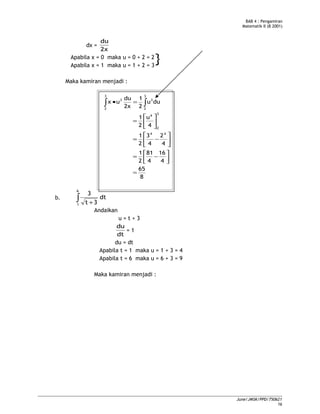
2.
( )∫ +
3
2
2
dz
12z
4z
2
June/JMSK/PPD/750621
17

18. BAB 4 : Pengamiran
Matematik II (B 2001)
Andaikan
u = 2z2
+ 1
dz
du
= 4z
dz =
4z
du
Apabila z = 0 maka u = 2(2) 2
+ 1 = 9
Apabila z = 1 maka u = 2(3) 2
+ 1 = 19
Maka kamiran menjadi :
171
10
171
199-
9
1
19
1
u
1
1-
u
duu
du
u
1
4z
du
u
4z
19
9
19
9
1-
19
9
2-
19
9
2
19
9
2
=
+
=




+−=




−=






=
=
=•
∫
∫∫
3. ( )∫ +
2
1-
43
dt15tt
Andaikan
u = 5t4
+ 1
dt
du
= 20t3
dt = 3
20t
du
Apabila t = -1 maka u = 5(-1)4
+ 1 = 6
Apabila t = 2 maka u = 5(2)4
+ 1 = 81
Maka kamiran menjadi :
June/JMSK/PPD/750621
18

19. BAB 4 : Pengamiran
Matematik II (B 2001)
8
1
163
40
6525
2
6525
20
1
2
36
2
6561
20
1
2
6
2
81
20
1
2
u
20
1
duu
20
1
20t
du
ut
22
81
6
2
81
6
81
6
3
3
=
=




=




−=






−=






=
=• ∫∫
4. dk
1k
k
3
0
2∫ +
Andaikan
u = k2
+ 1
dk
du
= 2k
dk =
2k
du
Apabila k = 0 maka u = 1
Apabila k = 3 maka u = 4
Maka kamiran menjadi :
June/JMSK/PPD/750621
19

20. BAB 4 : Pengamiran
Matematik II (B 2001)
[ ]
1
1-2
14
u
2u
2
1
2
1
u
2
1
duu
2
1
2k
du
u
k
dk
1k
k
4
1
2
1
4
1
2
1
4
1
2
1
4
1
2
1
1
3
0
2
=
=
−=






=






=










=
=
•=
+
∫
∫∫
−
4
SOALAN LATIHAN
1. Dengan menggunakan kaedah kamiran berhad, kamirkan setiap yang berikut:
a) ( )∫ +
2
0
dx1x b) ( )∫ −
3
1
2
dx3x2x
c) ( )∫ −
0
2-
2
dxx2x d) ( )∫ −
4
2
2
dx3xx
e) ( )∫ −
0
2-
2
dxxxkos f) ( )∫ +
3
0
2
dxxtan2
2. Dengan menggunakan kaedah kamiran berhad, kamirkan setiap yang berikut:
a) ( )∫ +
2
0
42
dx3x2x b) ( )∫ −
3
0
4
dxx3x3
c)
( )∫ +
0
2- 2
dx
53x
6x
2
d)
∫
3
1 2
dx
2-x
x
June/JMSK/PPD/750621
20