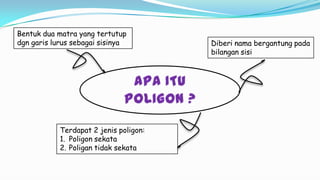
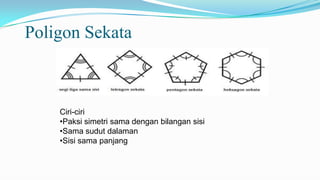
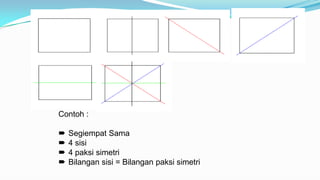
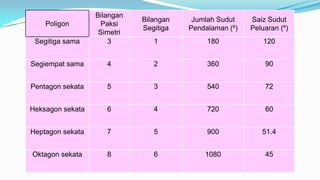
Dokumen tersebut membahas tentang poligon sekata dan tidak sekata, termasuk definisi, ciri-ciri, cara menghitung sudut dalam, perimeter, dan luas. Poligon dibedakan menjadi dua jenis berdasarkan panjang sisi dan besar sudut dalamnya. Rumus-rumus untuk menghitung sudut, perimeter, dan luas dipaparkan dengan beberapa contoh.

1.  TAKRIF POLIGON
 SUDUT DALAM POLIGON SEKATA DAN TIDAK SEKATA
 LUAS DAN PERIMETER POLIGON

2. Bentuk dua matra yang tertutup
dgn garis lurus sebagai sisinya Diberi nama bergantung pada
bilangan sisi
Terdapat 2 jenis poligon:
1. Poligon sekata
2. Poligan tidak sekata

3. Poligon Sekata
Ciri-ciri
•Paksi simetri sama dengan bilangan sisi
•Sama sudut dalaman
•Sisi sama panjang

4.  Bilangan paksi simetri sebuah poligon sekata adalah
sama dengan bilangan sisinya.
Contoh :
Segitiga Sisi Sama
 3 sisi
 3 paksi simetri
 Bilangan sisi = Bilangan paksi simetri

5.  Poligon yang mempunyai sisi yang sama panjang dan
sudut pedalaman yang sama besar.
Contoh :

6. Contoh :
 Segiempat Sama
 4 sisi
 4 paksi simetri
 Bilangan sisi = Bilangan paksi simetri

7. Mengira sudut dalaman poligon sekata
 Hasil tambah sudut pedalaman sebuah segitiga
=180 darjah
 Sebuah poligon yang mempunyai n sisi boleh dibahagikan kepada (n -
2) segitiga
 Hasil tambah sudut pedalamannya = (n - 2) x 180 darjah

8. Poligon
Bilangan
Paksi
Simetri
Bilangan
Segitiga
Jumlah Sudut
Pendalaman (º)
Saiz Sudut
Peluaran (º)
Segitiga sama 3 1 180 120
Segiempat sama 4 2 360 90
Pentagon sekata 5 3 540 72
Heksagon sekata 6 4 720 60
Heptagon sekata 7 5 900 51.4
Oktagon sekata 8 6 1080 45

9. Poligon Tak Sekata
 Sisi yang tidak sama panjang
 Sudut pedalaman yang berbeza
 Bilangan paksi simetri bergantung kepada bentuk

10. Mengira sudut dalaman poligon tak sekata
 Hasil tambah sudut pedalamannya = (n - 2) x 180 darjah
 Bagi polygon tak sekata, kita hanya dapat mengira hasil tambah sudut
pedalaman poligon.

11.  Perimeter --- panjang sisi yang mengelilingi bentuk-2D
 Untuk mendapat perimeter poligon sekata dan tidak sekata, hanya
perlu menambah kesemua panjang sisi poligon

12. CONTOHNYA
Perimeter = 4 + 3 + 3 + 4 + 3 + 3
= 20 cm
Perimeter = 7 + 5 +4 +5 +3
= 24 cm

13. o Luas – size permukaan 2D
o Menghitung luas dengan rumus tertentu
 Segi empat – lebar x panjang
 Segi tiga - x tapak x tinggi
 Trapezium - (a+b) x tinggi
2
1
2
1

14.  Poligon terdiri daripada beberapa segi tiga sama sisi.
 Untuk menghitung luasnya, kita hendaklah menghitung luas segi tiga dan
tambah kesemua luas.
 Seperti dalam gambar rajah, heksagon mempunyai 6 bucu dan terdiri
daripada 6 segi tiga sama sisi. Oleh itu,
Luas hexagon = x a x t x 6
2
1

15.  Bagaimana pula jika maklumat yang diberi tidak merangkumi tapak atau
tinggi segi tiga?
 Untuk pengetahuan anda, kita hanya memerlukan salah satu daripada
panjang sisi, jejari, atau apothem untuk mendapatkan luasnya
Jejari = radius = panjang dari pusat
bulatan (center) ke salah satu bucu
Apothem = panjang dari pusat bulatan
ke titik tengah salah satu sisi

16. KES 1 : PANJANG SISI DIBERI
 Gambar rajah tersebut merupakan salah satu segi tiga yang dikeluarkan
daripada poligon.
 Segi tiga bersudut tegak dibentuk apabila satu garis,h dilukis dari bucu
ke titik tengah sisi.
 Sudut pada bucu adalah bergantung pada bilangan sisinya ,n (bilangan sigi tiga). Dengan itu ,
sudut dan atau
 . Susun semula dan mendapat
 Luas bagi segi tiga = dan darab n bagi n segi tiga dalam poligon .
Luas poligon =
n
t
360
2
n
t
2
360
n
t
180
t
s
h
tan2
t
s
s
tan22
1
h
s
t 2tan

17. KES 2 : JEJARI DIBERI
 Seperti dengan kes 1, gambar rajah tersebut merupakan segi tiga yang
dikeluarkan daripada poligon
 Daripada segi tiga tersebut, kita dapat mengetahui :
 Luas segi tiga =
 Menggantikan hx, luas segi tiga = atau
 Dengan identiti trigo, kita mendapat
 Sudut 2t bergantung pada bilangan sisi,n~~ dan dapat
 Darab n bagi n segi tiga dalam poligon. Oleh itu,
luas poligon =
trh cos trx sin
hxxh 2
2
1
trtr sincos
n
360

18. KES 3 : APOTHEM DIBERI
 Sama keadaan dengan kes 1,
 dan tan t boleh ditulis sebagai
n
t
180
a
s
a
s
n 2
2180
tan
 Susun semula dan dapat
 Luas segi tiga =
 Menggantikan s, luas segi tiga = =
 Darab n bagi n sigi tiga dalam poligon tersebut,
Luas poligon =
n
as
180
tan2
as
2
1
2
180
tan2 a
n
a

19.  Kesimpulan luas poligon sekata :
 Jika panjang sisi,s diberi,
 Jika jejari,r diberi,
 Jika apothem,a diberi,