Downloaded 227 times
Uploaded byAishah Ya'Acob
Kalkulus asas terbitan pertama
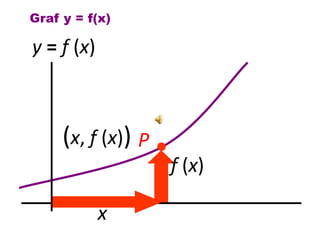
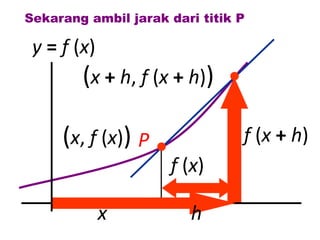
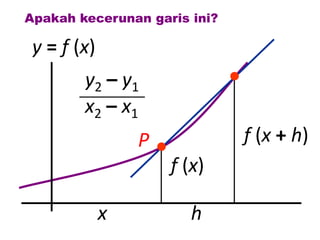
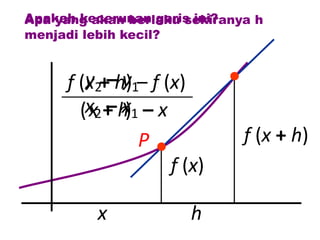
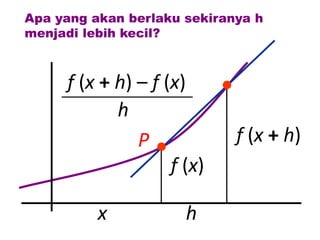
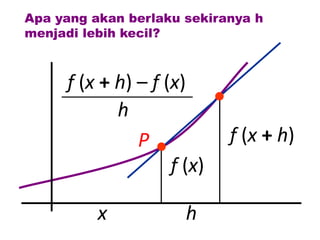
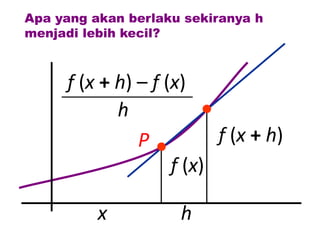
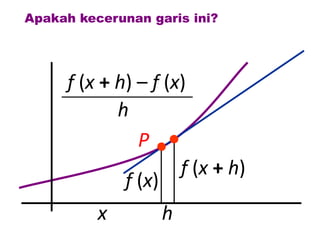
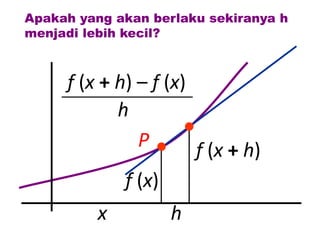
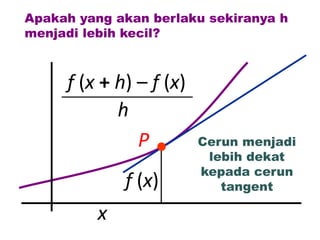
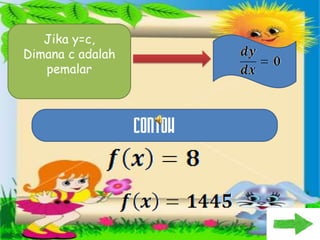
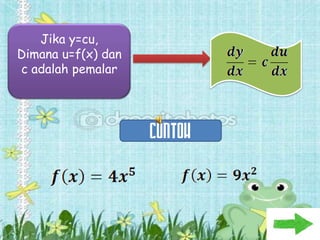
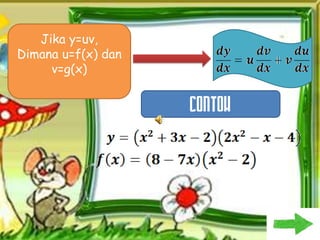
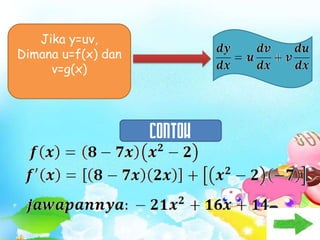
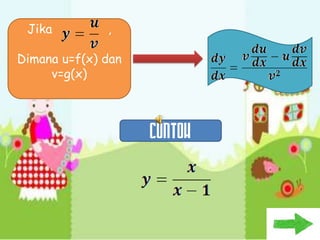
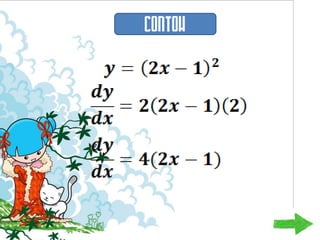
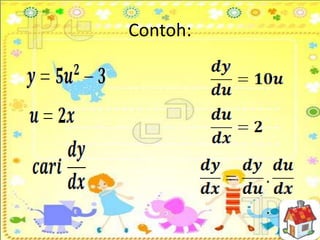
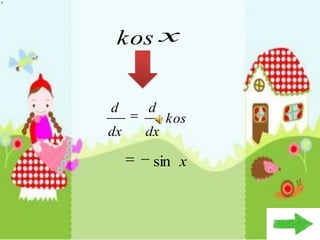
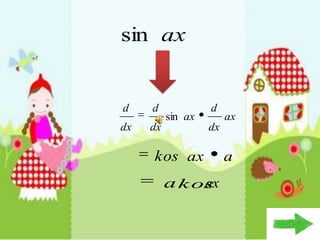
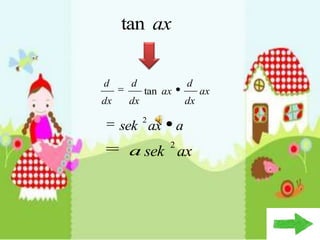
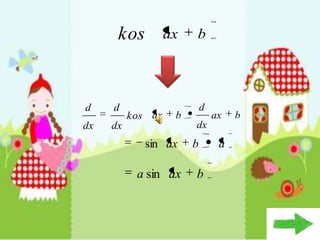
Dokumen ini membahas tentang konsep pembezaan dalam matematik, termasuk penggunaan prinsip pertama untuk mencari pembezaan fungsi. Berbagai contoh diberikan untuk ilustrasi, termasuk fungsi tetap dan fungsi yang melibatkan pemalar. Terdapat juga penjelasan tentang rumus rantaian dan aplikasinya dalam pembezaan.
More Related Content
Kalkulus asas terbitan pertama
- 2. Ayuh kita belajar bersama-sama
- 4. Menu Sila tekan pembezaan mengikut turutan PENGENALAN KONSEP RUMUS FUNGSI TRIGO LATIHAN
- 5. PENGENALANTerbitan Pertama sesuatu fungsi boleh didapati dengan menggunakan kaedah: PRINSIP PERTAMA RUMUS PEMBEZAAN
- 7. Graf y =f(x) y = f (x) (x, f (x)) P f (x) x
- 8. Sekarang ambil jarakdari titik P y = f (x) (x + h, f (x + h)) (x, f (x)) P f (x + h) f (x) x h
- 9. Apakah kecerunan garisini? y = f (x) y2 – y1 x2 – x1 P f (x + h) f (x) x h
- 10. Apakah kecerunan garisini? Apa yang akan berlaku sekiranya h menjadi lebih kecil? f (x2+–h)1– f (x) y y (x2 + h)1 – x x –x P f (x + h) f (x) x h
- 11. Apa yang akanberlaku sekiranya h menjadi lebih kecil? f (x + h) – f (x) h P f (x + h) f (x) x h
- 12. Apa yang akanberlaku sekiranya h menjadi lebih kecil? f (x + h) – f (x) h P f (x + h) f (x) x h
- 13. Apa yang akanberlaku sekiranya h menjadi lebih kecil? f (x + h) – f (x) h P f (x + h) f (x) x h
- 14. Apakah kecerunan garisini? f (x + h) – f (x) h P f (x + h) f (x) x h
- 15. Apakah yang akanberlaku sekiranya h menjadi lebih kecil? f (x + h) – f (x) h P f (x + h) f (x) x h
- 16. Apakah yang akanberlaku sekiranya h menjadi lebih kecil? f (x + h) – f (x) h P Cerun menjadi lebih dekat kepada cerun f (x) tangent x
- 17. Rumus Penting! f’(x)= had f (x + h) – f (x) h→0 h
- 18. Contoh 1: Dapatkan pembezaan PRINSIPPERTAMA bagi fungsi f(x)=x
- 19.
- 20. Contoh 2: Dapatkanpembezaan PRINSIP PERTAMA bagi fungsi
- 23. Jika y=c, Dimana cadalah pemalar CONTOH
- 24. Jika , CONTOH
- 25. Jika y=cu, Dimana u=f(x)dan c adalah pemalar CONTOH
- 26. Jika y=uv, Dimana u=f(x)dan v=g(x) CONTOH
- 27. Jika y=uv, Dimana u=f(x)dan v=g(x) CONTOH
- 28. Jika , Dimana u=f(x) dan v=g(x) CONTOH
- 29.
- 30. Jika , CONTOH
- 31.
- 32. Rumus Rantaian • Jikay dinyatakan dalam sebutan u, y=f(u), dan u dinyatakan dalam sebutan x, u=g(x), maka y dapat dinyatakan dalam sebutan x, iaitu y=f(u) = f(g(x)) • Contoh:
- 33.
- 34. kos x Sin x tan x Sin ax kos ax tan ax Tan Sin (ax+b) (ax+b) Kos (ax+b)
- 35. sin x d d sin x dx dx kos x
- 36. x kos x d d kos dx dx sin x
- 37. tan x d d tan x dx dx 2 sek x
- 38. sin ax d d d sin ax ax dx dx dx kos ax a a k osx a
- 39. kos ax d d d kos ax ax dx dx dx sin ax a a sin ax
- 40. tan ax d d d tan ax ax dx dx dx 2 sek ax a 2 a sek ax
- 41. sin ax b d d d sin ax b ax b dx dx dx kos ax b a a kos ax b
- 42. kos ax b d d d kos ax b ax b dx dx dx sin ax b a a sin ax b
- 43. tan ax b d d d tan ax b ax b dx dx dx 2 sek ax b a 2 a sek ax b
- 44. Apakah pembezaan bagi f(x) berikut? • 1) f (x) = x 2 • 2)
- 45. • Penyelesai 1) f (x) = x 2 an f (x ) = x 2 F (x + h) = (x + h)2 = x 2 + 2xh + h 2 f’(x)= had f (x + h) – f (x) h→0 h
- 46.