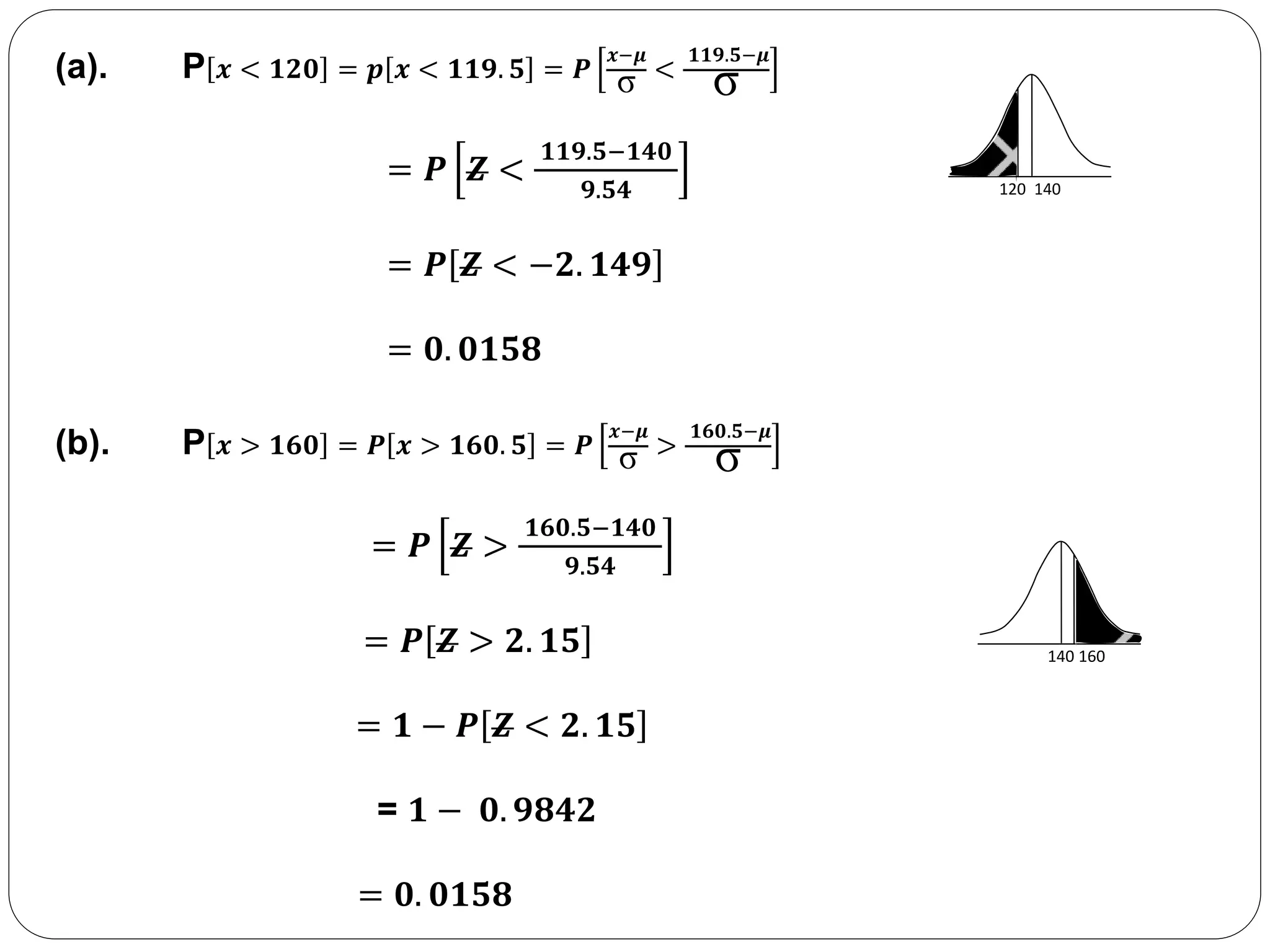
This document discusses using the normal distribution to approximate the binomial distribution when n is large and p is around 0.5. It provides continuity correction rules for using the normal approximation. It then works through an example calculating the probability of different outcomes when sampling 400 seeds with a 0.35 probability of being ryegrass. It calculates the probabilities using the normal approximation and continuity corrections.

1. Normal Approximation
to
The Binomial Distribution
NADEEM UDDIN
ASSOCIATE PROFESSOR
OF STATISTICS

2. Use of Normal Approximation to The Binomial Distribution
We can use the normal distribution as a close approximation
to the binomial distribution when n is large and
p is moderate (not to far from 0.5) .
OR
We can use the normal distribution as a close approximation
to the binomial distribution whenever n×p ≥ 5 and n×q ≥ 5.

3. As we know that the binomial distribution is a discrete distribution and
the normal distribution is a continuous distribution, When we use
normal approximation we should use the following continuity
correction rules.
(i) P(x1 ≤ X ≤ x2) = P(x1- 0.5 < X < x2+ 0.5)
(ii) P(x1 < X < x2) = P(x1+ 0.5 < X < x2- 0.5)
(iii) p(X > x) = p(X > x+0.5)
(iv) p(X ≥ x) = p(X > x – 0.5)
(v) p(X < x) = p(X < x – 0.5 )
(vi) p(X ≤ x) = p(X < x+0.5)
(vii) p(X = x) = P(x1- 0.5 < X < x2+ 0.5)

5. Example-4
In a sack of mixed grass seeds, the probability that a seed is
ryegrass is 0.35, find the probability that in a random
sample of 400 seeds from this sack,
(a). less than 120 are ryegrass seeds,
(b). more than 160 are ryegrass seeds,
(c). between 120 and 150 are ryegrass
(d). 150 are ryegrass.
Solution:
n = 400 ; p = 0.35
µ = np = 400 × 0.35 = 140
σ = 𝑛𝑝𝑞 = 400 × 0.35 × 0.65 = 9.54

6. (a). P 𝒙 < 𝟏𝟐𝟎 = 𝒑 𝒙 < 𝟏𝟏𝟗. 𝟓 = 𝑷
𝒙−𝝁
σ <
𝟏𝟏𝟗.𝟓−𝝁
σ
= 𝑷 𝒁 <
𝟏𝟏𝟗.𝟓−𝟏𝟒𝟎
𝟗.𝟓𝟒
= 𝑷 𝒁 < −𝟐. 𝟏𝟒𝟗
= 𝟎. 𝟎𝟏𝟓𝟖
(b). P 𝒙 > 𝟏𝟔𝟎 = 𝑷 𝒙 > 𝟏𝟔𝟎. 𝟓 = 𝑷
𝒙−𝝁
σ >
𝟏𝟔𝟎.𝟓−𝝁
σ
= 𝑷 𝒁 >
𝟏𝟔𝟎.𝟓−𝟏𝟒𝟎
𝟗.𝟓𝟒
= 𝑷 𝒁 > 𝟐. 𝟏𝟓
= 𝟏 − 𝑷 𝒁 < 𝟐. 𝟏𝟓
= 𝟏 − 𝟎. 𝟗𝟖𝟒𝟐
= 𝟎. 𝟎𝟏𝟓𝟖
120 140
140 160

7. (c).
P 120 < 𝑥 < 150 = 𝑃 120.5 < 𝑥 < 149.5
= 𝑃
120.5−140
9.54
< 𝑍 <
149.5−140
9.54
= 𝑃 −2.04 < 𝑍 < 0.99
= 𝑃 0 < 𝑍 < 0.99 − 𝑃 −2.04 < 𝑍 < 0
= 0.8389 − 0.0207
= 0.8182
120 140 150

8. (d) P x = 150 = P 149.5 < x < 150.5
P x = 150 = P
149.5−μ
σ
<
x−μ
σ
<
150.5−μ
σ
P x = 150 = P
149.5−140
9.54
< Z <
150.5−140
9.54
P x = 150 = P 0.99 < Z < 1.10
P x = 150 = P Z < 1.10 − P Z < 0.99
P x = 150 = 0.8643 − 0.8389
P x = 150 = 0.0254
140 149.5 150.5