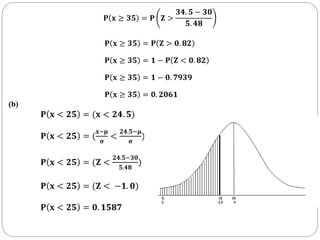
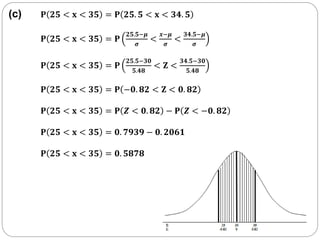
This document discusses using the normal distribution to approximate the Poisson distribution when the mean is large (greater than 15). It provides continuity correction rules for converting between discrete and continuous probabilities. As an example, it calculates the probability of the number of accidents exceeding or falling below certain thresholds over 10 months, assuming accidents follow a Poisson distribution with a mean of 3 per month.

1. NADEEM UDDIN
ASSOCIATE PROFESSOR
OF STATISTICS
Normal Approximation
to
The Poisson Distribution

2. Use of Normal Approximation to The Poisson Distribution
We can use the normal distribution as a close approximation to
the
Poisson distribution whenever Mean is large (more than 15).
As we know that the Poisson distribution is a discrete distribution
and the normal distribution is a continuous distribution, When we
use normal approximation we should use the following continuity
correction rules.
(i) P(x1 ≤ X ≤ x2) = P(x1- 0.5 < X < x2+ 0.5)
(ii) P(x1 < X < x2) = P(x1+ 0.5 < X < x2- 0.5)
(iii) p(X > x) = p(X > x+0.5)
(iv) p(X ≥ x) = p(X > x – 0.5)
(v) p(X < x) = p(X < x – 0.5 )
(vi) p(X ≤ x) = p(X < x+0.5)
(vii) p(X = x) = P(x1- 0.5 < X < x2+ 0.5)

4. Example-5
In a certain city area the number of accidents occurring in a month
follows a Poisson distribution with mean 3. Find the following
probability that there will be accidents during 10 months.
(a) at least 35 accidents
(b) Less 30 accidents
(c) Between 25 and 35
(d) 35 accidents.
Solution:
µ = 3×10 = 30 (in 10 months)
As we know in Poisson distribution mean is equal to variance
Therefore 𝛔 𝟐 = 𝟑𝟎
σ = 5.48
(a) 𝐏 𝐱 ≥ 𝟑𝟓 = 𝐏 𝐱 > 𝟑𝟒. 𝟓
𝐏 𝐱 ≥ 𝟑𝟓 = 𝐏
𝐱−𝛍
𝛔
>
𝟑𝟒.𝟓−𝛍
𝛔

5. 𝐏 𝐱 ≥ 𝟑𝟓 = 𝐏 𝐙 >
𝟑𝟒. 𝟓 − 𝟑𝟎
𝟓. 𝟒𝟖
𝐏 𝐱 ≥ 𝟑𝟓 = 𝐏 𝐙 > 𝟎. 𝟖𝟐
𝐏 𝐱 ≥ 𝟑𝟓 = 𝟏 − 𝐏 𝐙 < 𝟎. 𝟖𝟐
𝐏 𝐱 ≥ 𝟑𝟓 = 𝟏 − 𝟎. 𝟕𝟗𝟑𝟗
𝐏 𝐱 ≥ 𝟑𝟓 = 𝟎. 𝟐𝟎𝟔𝟏
(b)
𝐏 𝐱 < 𝟐𝟓 = (𝐱 < 𝟐𝟒. 𝟓)
𝐏 𝐱 < 𝟐𝟓 = (
𝐱−𝛍
𝛔
<
𝟐𝟒.𝟓−𝛍
𝛔
)
𝐏 𝐱 < 𝟐𝟓 = (𝐙 <
𝟐𝟒.𝟓−𝟑𝟎
𝟓.𝟒𝟖
)
𝐏 𝐱 < 𝟐𝟓 = (𝐙 < −𝟏. 𝟎)
𝐏 𝐱 < 𝟐𝟓 = 𝟎. 𝟏𝟓𝟖𝟕

6. (c) 𝐏 𝟐𝟓 < 𝐱 < 𝟑𝟓 = 𝐏 𝟐𝟓. 𝟓 < 𝐱 < 𝟑𝟒. 𝟓
𝐏 𝟐𝟓 < 𝐱 < 𝟑𝟓 = 𝐏
𝟐𝟓.𝟓−𝝁
𝝈
<
𝒙−𝝁
𝝈
<
𝟑𝟒.𝟓−𝝁
𝝈
𝐏 𝟐𝟓 < 𝐱 < 𝟑𝟓 = 𝐏
𝟐𝟓.𝟓−𝟑𝟎
𝟓.𝟒𝟖
< 𝐙 <
𝟑𝟒.𝟓−𝟑𝟎
𝟓.𝟒𝟖
𝐏 𝟐𝟓 < 𝐱 < 𝟑𝟓 = 𝐏 −𝟎. 𝟖𝟐 < 𝐙 < 𝟎. 𝟖𝟐
𝐏 𝟐𝟓 < 𝐱 < 𝟑𝟓 = 𝐏 𝒁 < 𝟎. 𝟖𝟐 − 𝐏 𝒁 < −𝟎. 𝟖𝟐
𝐏 𝟐𝟓 < 𝐱 < 𝟑𝟓 = 𝟎. 𝟕𝟗𝟑𝟗 − 𝟎. 𝟐𝟎𝟔𝟏
𝐏 𝟐𝟓 < 𝐱 < 𝟑𝟓 = 𝟎. 𝟓𝟖𝟕𝟖

7. (d) P x = 35 = P 34.5 < x < 35.5
P x = 35 = P
34.5−μ
σ
<
x−μ
σ
<
35.5−μ
σ
P x = 35 = P
34.5−30
5.48
< Z <
35.5−30
5.48
P x = 35 = P 0.82 < Z < 1.00
P x = 35 = P Z < 1.00 − P Z < 0.82
P x = 35 = 0.8413 − 0.7939
P x = 35 = 0.0474 30 34.5 35.5