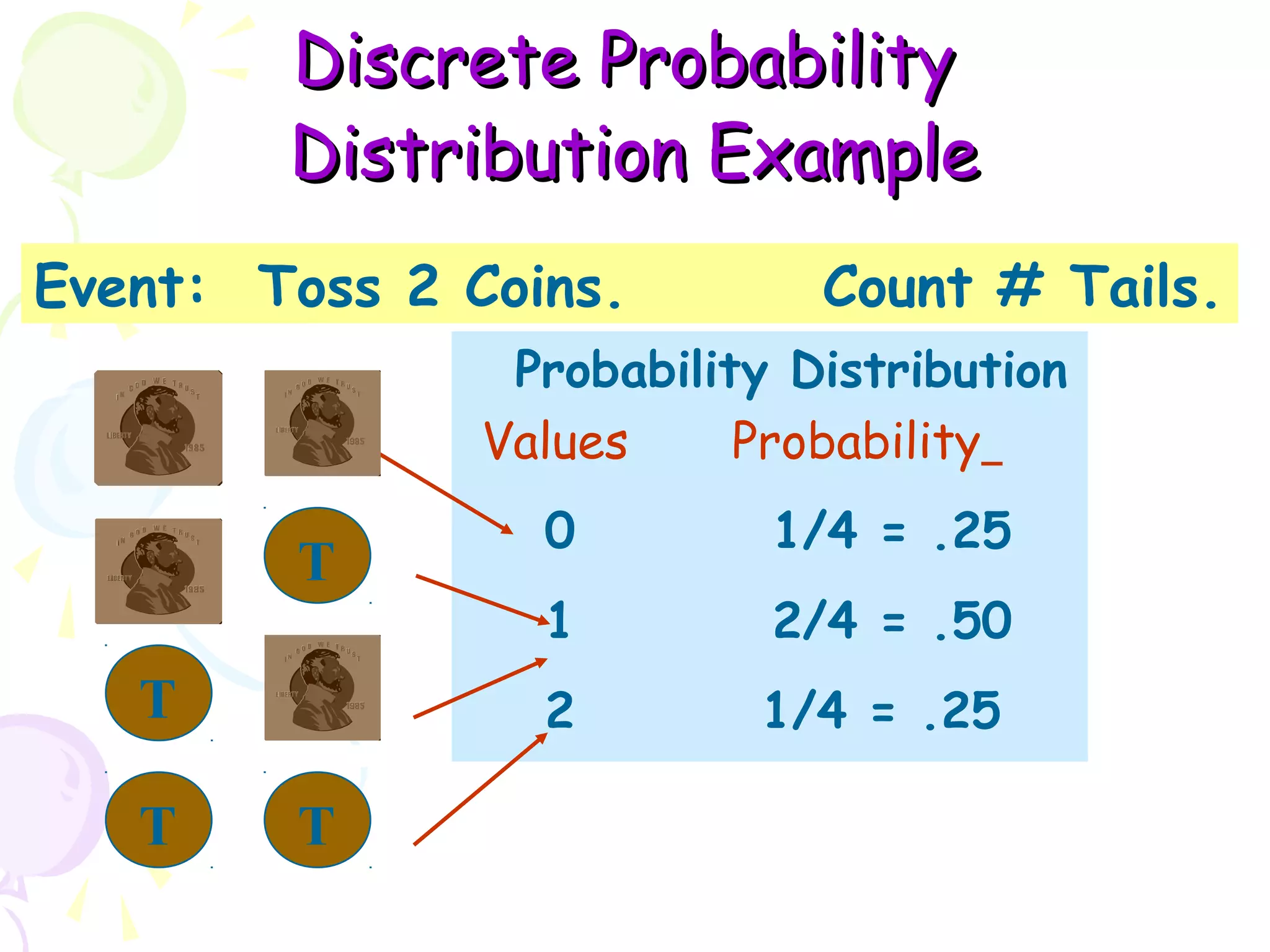
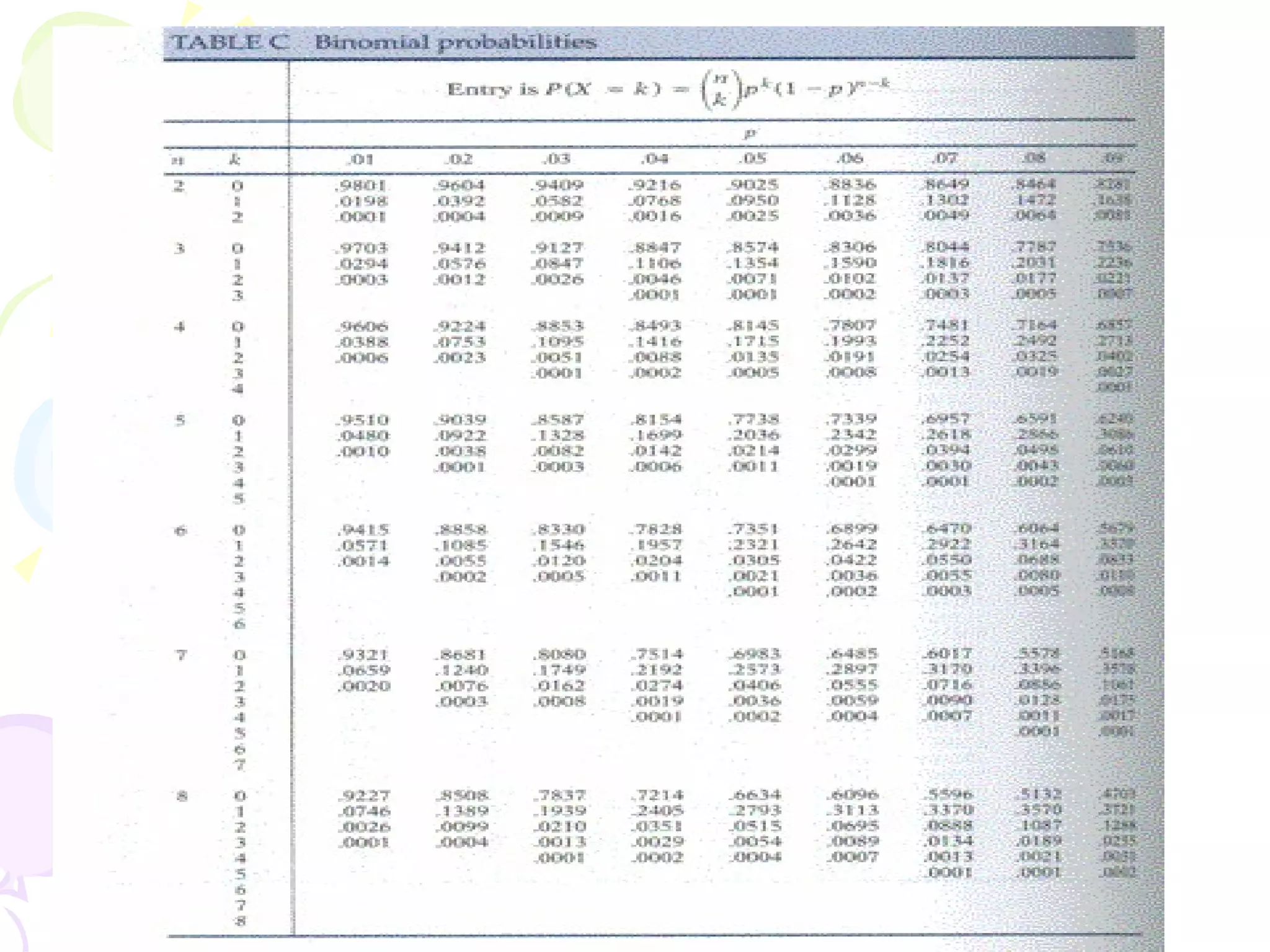
This document provides information on probability distributions, including discrete and binomial distributions. It discusses the assumptions and characteristics of binomial distributions, using examples to show how they work. It also covers the Poisson distribution, its assumptions and function, and gives an example of calculating probabilities using the Poisson. The document ends with questions for practice with binomial and Poisson distributions.

1. PPrroobbaabbiilliittyy
DDiissttrriibbuuttiioonnss

2. RRaannddoomm VVaarriiaabbllee
• Random variable
– Outcomes of an experiment
expressed numerically
– e.g.: Throw a die twice; Count the
number of times the number 6
appears (0, 1 or 2 times)

3. DDiissccrreettee RRaannddoomm VVaarriiaabbllee

4. DDiissccrreettee PPrroobbaabbiilliittyy
DDiissttrriibbuuttiioonn EExxaammppllee
Event: Toss 2 Coins. Count # Tails.
Probability Distribution
Values Probability
0 1/4 = .25
1 2/4 = .50
2 1/4 = .25
T
T
T T

5. Discrete Probability
Distributions
Binomial Poisson

6. BBiinnoommiiaall DDiissttrriibbuuttiioonn- AAssssuummppttiioonnss
• “n” Identical & finite trials
– e.g.: 15 tosses of a coin; 10 light bulbs taken from a
warehouse
• Two mutually exclusive outcomes on each
trial
– e.g.: Heads or tails in each toss of a coin; defective or
not defective light bulb
• Trials are independent of each other
– The outcome of one trial does not affect the outcome of
the other.
• Constant probability for each trial
– e.g.: Probability of getting a tail is the same each time a
coin is tossed

7. BBiinnoommiiaall DDiissttrriibbuuttiioonn
• A random variable X is said to follow
Binomial distribution if it assumes only
non negative values and its function is
given by
P x n !
- -
( ) ( ) x ( ) n x
= p 1
p
X x n -
x
! !
• x: No. of “successes” in a sample,
x=0,1,2..,n.
• n: Number of trials.
• p: probability of each success.
• q: probability of each failure (q=1-p)
•Notation: X ~ B (n, p).

8. BBiinnoommiiaall
DDiissttrriibbuuttiioonn CChhaarraacctteerriissttiiccss
• Mean
EX:
m = E ( X ) = np
m = np = 5( .1) = .5
• Variance and
standard deviation-
Ex:
n = 5 p = 0.1
.6
.4
.2
0
0 1 2 3 4 5
X
P(X)
( )
( )
2 1
np p
np 1
p
s = np(1- p) = 5( .1) (1-.1) = .6708
s
s
= -
= -

9. EExxaammppllee
• The experiment: Randomly draw red ball with
replacement from an urn containing 10 red balls
and 20 black balls.
• Use S to denote the outcome of drawing a red
ball and F to denote the outcome of a black ball.
• Then this is a binomial experiment with p =1/3.
• Q: Would it still be a binomial experiment if the
balls were drawn without replacement?

10. QQuueessttiioonnss ffoorr pprraaccttiiccee
• Ten coins are thrown simultaneously. Find the
probability of getting at least seven heads.
• A & B play a game in which their chances of winning are
in the ratio 3:2. find A’s chance of winning at least 3
games out of the 5 games played.
• Mr. Gupta applies for a personal loan of Rs 150,000
from a nationalized bank to repair his house. The loan
offer informed him that over the years bank has
received about 2920 loan applications per year and that
the prob. Of approval was on average, about 0.85. Mr.
Gupta wants to know the average and standard
deviation of the number of loans approved per year.

11. • The incidence of a certain disease in
such that on the average 20% of workers
suffer from it. If 10 workers are
selected at random, find the probability
that
1. Exactly 2 workers suffer from the
disease.
2. Not more than 2 workers suffer from
the disease.
• Bring out the fallacy, if any
1. The mean of a binomial distribution is 15
and its standard deviation is 5.
2. Find the binomial distribution whose
mean is 6 and variance is 4.

12. • The probability that an evening college student
will be graduate is 0.4.Determine the probability
that out of 5 students
• None will be graduate.
• One will be graduate.
• At least one will be graduate.
• Multiple choice test consists of 8 questions and
three answers to each question (of which only
one is correct). A student answers each question
by rolling a balanced die and marking the first
answer if he gets 1 or 2, the second answer if he
gets 3 or 4 and the third answer if he gets 5 or
6. To get a distinction, student must secure at
least 75% correct answers.If there is no
negative marking, what is the probability that
student secures a distinction?

13. Q. Assuming that half the population are
Consumers of rice and assuming that 100
investigators can take sample of 10
individuals to see whether they are rice
consumers , how many investigations
would you expect to report that three
people or less were consumers of rice?
Q. Five coins are tossed 3200 times. Find
the frequencies of the distribution of
heads and tails and tabulate the result.
Also calculate the mean number of
successes and S.D.

14. CCrreeddiitt CCaarrdd EExxaammppllee
• Records show that 5% of the customers in a
shoe store make their payments using a credit
card.
• This morning 8 customers purchased shoes.
• Use the binomial table to answer the following
questions.
1. Find the probability that exactly 6 customers
did not use a credit card.
2. What is the probability that at least 3
customers used a credit card?

15. CCrreeddiitt CCaarrdd EExxaammppllee
3. What is the expected number of customers
who used a credit card?
4. What is the standard deviation of the
number of customers who used a credit
card?

16. PPaarrkkiinngg EExxaammppllee
• Sarah drives to work everyday, but does not own a parking
permit. She decides to take her chances and risk getting a
parking ticket each day. Suppose
– A parking permit for a week (5 days) cost $ 30.
– A parking fine costs $ 50.
– The probability of getting a parking ticket each day is
0.1.
– Her chances of getting a ticket each day is independent
of other days.
– She can get only 1 ticket per day.
• What is her probability of getting at least 1 parking ticket
in one week (5 days)?
• What is the expected number of parking tickets that Sarah
will get per week?
• Is she better off paying the parking permit in the long run?

18. BBiinnoommiiaall DDiissttrriibbuuttiioonn-
DDiiffffeerreenntt ssiittuuaattiioonnss
Random experiments and random variable

19. SSiittuuaattiioonnss CCoonnttdd....
Random experiments and random variables

20. PPooiissssoonn
DDiissttrriibbuuttiioonn

21. AAssssuummppttiioonnss
Applicable when-
1) No. of trials is indefinitely large n®¥
2) Probability of success p for each trial
is very small. p ®0
3) Mean is a finite number given by
np = l

22. PPooiissssoonn DDiissttrriibbuuttiioonn FFuunnccttiioonn
X P ( X
)
e X
!
( )
P X X
X
: probability of "successes" given
: number of "successes" per unit
: expected (average) number of "successes"
: 2.71828 (base of natural logs)
e
ll
l
l
-
= X =0,1,2…
X ~ P(l)

23. PPooiissssoonn DDiissttrriibbuuttiioonn
CChhaarraacctteerriissttiiccss
( )
m l
= =
=å
( )
E X
N
1
i i
i
X P X
=
• Mean
• Variance & Standard deviation
s 2 =l s = l

24. Example
Arrivals at a bus-stop follow a
Poisson distribution with an
average of 4.5 every quarter of
an hour.
(assume a maximum of 20
arrivals in a quarter of an hour)
and calculate the probability of
fewer than 3 arrivals in a
quarter of an hour.

25. The probabilities of 0 up to 2 arrivals can
be calculated directly from the formula
-ll
x p ()
x
e !
x
=
4.504.5 (0)
0!
p e
-
=
with l =4.5
So p(0) = 0.01111

26. Similarly p(1)=0.04999 and p(2)=0.11248
So the probability of fewer than 3 arrivals is
0.01111+ 0.04999 + 0.11248 =0.17358

27. QQuueessttiioonnss ffoorr pprraaccttiiccee
• Suppose on an average 1 house in 1000 in a
certain district has a fire during a year.If
there are 2000 houses in that district,what is
the probability that exactly 5 houses will have
a fire during the year?
• If 3% of the electric bulbs manufactured by
a company are defective, find the probability
that in a sample of 100 bulbs
a) 0 b) 5 bulbs c) more than 5
d) between 1 and 3
e) less than or equal to 2 bulbs are defective

28. • Comment on the following for a Poisson
distribution with Mean = 3 and s.D = 2
• In a Poisson distribution if p(2)= 2/3 p(1).
Find
i) mean ii) standard deviation
iii)P(3) iv) p(x > 3)
• A car hire firm has two cars, which it hires
out day by day.The number of demands for a
car on each day is distributed as a Poisson
distribution with mean 1.5. Calculate the
proportion of days on which
i) Neither car is used.
ii) Some demand is refused.

29. • A manufacturer who produces medicine
bottles,finds that 0.1% of the bottles are
defective. The bottles are packed in boxes
containing 500 bottles.A drug manufacturer
buys 100 boxes from the producer of
bottles.Find how many boxes will contain
i) no defectives
ii) at least two defectives
• The following table gives the number of days
in a 50 day period during which automobile
accidents occurred in a city-
No. of accidents: 0 1 2 3 4
No. of days : 21 18 7 3 1
Fit a Poisson distribution to data.

30. Note:
In most cases, the actual number of trials is
not known, only the average chance of
occurrence based on the past experience
can help in constructing the whole distribution .
For ex: The number of accidents in any
Particular period of time : the distribution
is based on the mean value of occurrence of
an event , which may also be obtained based
on Past Experience .

31. • In a town 10 accidents took place in a
span of 50 days. Assuming that the
number of accidents per day follow
Poisson distribution, find the probability
that there will be 3 or more accidents in
a day.
HINT:
l = 10/50 = 0.2
Average no. of accidents per day

32. • Case-Let
• An insurance company insures 4000
people against loss of both eyes in a car
accident.Based on previous data,the
rates were computed on the assumption
that on the average 10 persons in
1,00,000 will have car accident each
year that result in this type of
injury.What is the probability that more
than 4 of the insured will collect on a
policy in a given year?

33. PPooiissssoonn ttyyppee SSiittuuaattiioonnss
• Number of deaths from a disease.
• No. of suicides reported in a city.
• No. of printing mistakes at each page of a
book.
• Emission of radioactive particles.
• No. of telephone calls per minute at a small
business.
• No. of paint spots per new automobile.
• No. of arrivals at a toll booth
• No. of flaws per bolt of cloth