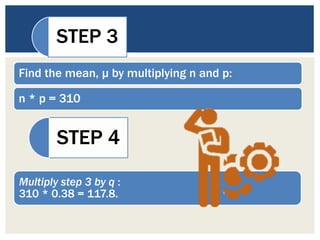
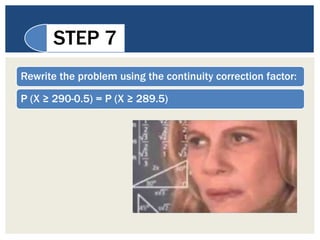
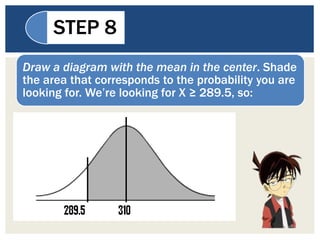
This document discusses the normal approximation to the binomial distribution. It explains that when the sample size (n) is large enough, the binomial distribution can be approximated by a normal distribution. It provides steps for using the normal approximation, including calculating n*p and n*q to determine if the approximation can be used, finding the mean and standard deviation, using the continuity correction factor, and looking up the probability in the z-table. An example problem demonstrates how to use these steps to calculate the probability that at least 290 students out of a sample of 500 are enrolled in school.

1. Prepared by:
Paul John Rey A. Tanghal
NORMAL
APPROXIMATION TO
BINOMIAL DISTRIBUTION

2. The normal approximation to the
binomial is when you use a continuous
distribution (the normal distribution) to
approximate a discrete distribution (the
binomial distribution). According to the
Central Limit Theorem, the sampling
distribution of the sample means
becomes approximately normal if the
sample size is large enough.
WHAT IS NORMAL APPROXIMATION TO
THE BINOMIAL DISTRIBUTION?

3. The first step into using the normal approximation to
the binomial is making sure you have a “large
enough sample”. How large is “large enough”? You
figure this out with two calculations: n * p and n * q .
The Uses of n*p and n*q

4. Where:
n is your sample size,
p is your given probability.
q is just 1 – p. For example, let’s say your probability p is .6.
You would find q by subtracting this probability from 1: q = 1
– .6 = .4. Percentages (instead of decimals) can make this a
little more understandable; if you have a 60% chance of it
raining (p) then there’s a 40% probability it won’t rain (q).
When n * p and n * q are greater than 5, you can use the
normal approximation to the binomial to solve a problem.

5. Sixty two percent of 12th
graders attend school in a
particular urban school
district. If a sample of 500
12th grade children are
selected, find the probability
that at least 290 are
actually enrolled in school.
NORMAL APPROXIMATION
EXAMPLE

6. Find p, q, and
n:
The
probability p
is given in the
question as
62%, or 0.62
To find q,
subtract p
from 1: 1 –
0.62 = 0.38
The sample
size n is given
in the
question as
500
MAKING CALCULATIONS
STEP 1

7. Figure out if you can use the
normal approximation to the
binomial. If n * p and n * q
are greater than 5, then you
can use the approximation:
n * p = 310 and n * q = 190.
These are both larger than 5,
so you can use the normal
approximation to the binomial
for this question.
STEP 2

8. Find the mean, μ by multiplying n and p:
n * p = 310
STEP 3
STEP 4
Multiply step 3 by q :
310 * 0.38 = 117.8.

9. Take the square root of
step 4 to get the standard
deviation,
σ:
√(117.8)=10.85
Note: The formula for the
standard deviation for a
binomial is √(n*p*q)
STEP 5

10. Write the problem using correct notation. The
question stated that we need to “find the probability
that at least 290 are actually enrolled in school”.
So:
P(X ≥ 290)
PART II: USING THE CONTINUITY
CORRECTION FACTOR
STEP 6

11. Rewrite the problem using the continuity correction factor:
P (X ≥ 290-0.5) = P (X ≥ 289.5)
STEP 7

12. Draw a diagram with the mean in the center. Shade
the area that corresponds to the probability you are
looking for. We’re looking for X ≥ 289.5, so:
STEP 8

13. Find the z-score.
You can find this by subtracting the mean (μ) from the
probability you found in step 7, then dividing by the standard
deviation (σ):
(289.5 – 310) / 10.85 = -1.89
STEP 9
STEP 10
Look up the z-value in the z-table:
The area for -1.89 is 0.4706.

14. Add .5 to your
answer in step 10
to find the total
area pictured:
0.4706 + 0.5 =
0.9706.
That’s it! The
probability is
.9706, or 97.06%.
STEP 11

15. References:
Stephanie Glen. "Normal Approximation to the Binomial" From
StatisticsHowTo.com: Elementary Statistics for the rest of us!
https://www.statisticshowto.com/probability-and-
statistics/binomial-theorem/normal-approximation-to-the-binomial/

16. END
E N D