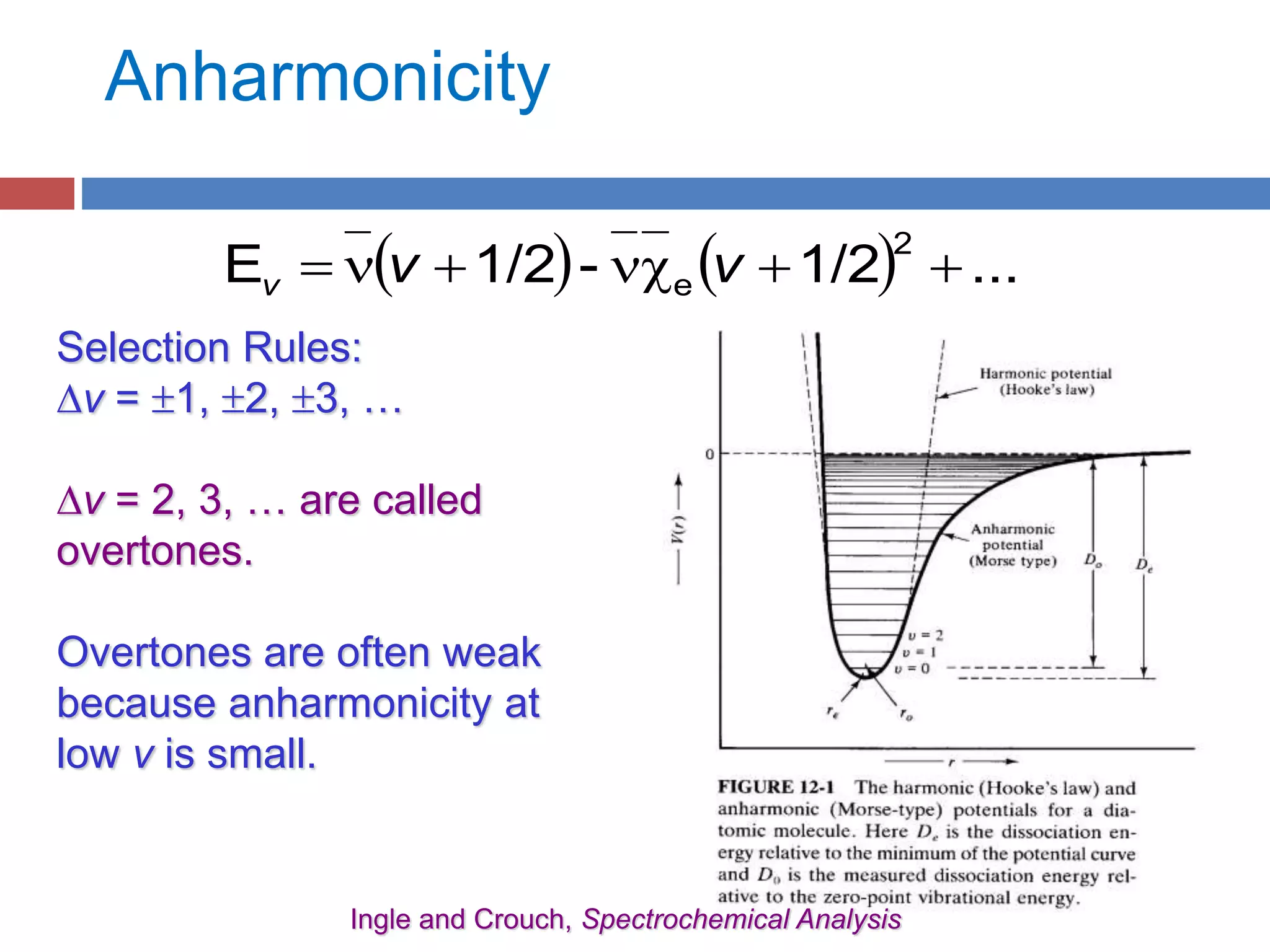
Rotational spectroscopy measures the energies of rotational states of molecules. It can observe the rotation of polar molecules using microwave or infrared spectroscopy, and of non-polar molecules using Raman spectroscopy. Molecules can be modeled as rigid or non-rigid rotors. Diatomic and linear molecules can be modeled as rigid rotors, while distortions are accounted for in non-rigid rotor models. Vibrational states are modeled as harmonic oscillators, though anharmonicity is considered. Rotational and vibrational states are quantized, and selection rules apply to rotational-vibrational transitions.

1. ASSIGNMENT ON
Non- Rigid Rotator

2. Rotational spectroscopy
 Rotational spectroscopy is concerned with the measurement of
the energies of transitions between quantized rotational states
of molecules in the gas phase. The spectra of polar molecules can
be measured in absorption or emission by microwave spectroscopy
or by far infrared spectroscopy.
 The rotational spectra of non-polar molecules cannot be observed
by those methods, but can be observed and measured by Raman
spectroscopy.
 Rotational spectroscopy is sometimes referred to as pure rotational
spectroscopy to distinguish it from rotational-vibrational
spectroscopy where changes in rotational energy occur together
with changes in vibrational energy, and also from ro-vibronic
spectroscopy where rotational, vibrational and electronic energy
changes occur simultaneously

3. Types of molecule
 Linear molecule
 Symmetric top Molecule
 Spherical top molecule
 Asymmetric top Molecule

4. Rotational Spectra
Simplest Case: Diatomic or Linear Polyatomic molecule
Rigid Rotor Model: Two nuclei joined by a weightless rod
J = Rotational quantum number (J = 0, 1, 2, …)
I = Moment of inertia = mr2
m = reduced mass = m1m2 / (m1 + m2)
r = internuclear distance
m1
m2
 1JJ
I2
E
2
J 


5. Rigid Rotor Model
In wavenumbers (cm-1):
 1JJ
Ic8
h
F 2J 

 1JJBFJ 
Separation between adjacent levels:
F(J) – F(J-1) = 2BJ

6. Rotational
Energy Levels
Selection Rules:
Molecule must have a
permanent dipole.
DJ = 1
J. Michael Hollas, Modern Spectroscopy,
John Wiley & Sons, New York, 1992.

7. The Non-Rigid Rotor
Account for the dynamic nature of the chemical bond:
DJ = 0, 1
  22
J 1)(JJ
hc
D
1JJ
hc
B
E 
D is the centrifugal distortion constant
(D is large when a bond is easily stretched)
Typically, D < 10-4*B and B = 0.1 – 10 cm-1
  22
J 1)(JJD1JJB F
m


k
c
D
2
1
and
B4
2
3


8. Vibrational Transitions
Simplest Case: Diatomic Molecule
Harmonic Oscillator Model: Two atoms connected by a
spring.
 1/2E  vv
 1/2hE  vv
v = vibrational quantum number (v = 0, 1, 2, …)
 = classical vibrational frequency
2/1
k
2
1






m

k = force constant (related to the bond order).
in Joules
in cm-1

9. Vibrational Energy Levels
J. Michael Hollas, Modern Spectroscopy, John Wiley & Sons, New York, 1992.
Selection Rules:
1) Must have a change in dipole moment (for IR).
2) Dv = 1

10. Anharmonicity
Ingle and Crouch, Spectrochemical Analysis
    ...1/2-1/2E
2
e  vvv
Selection Rules:
Dv = 1, 2, 3, …
Dv = 2, 3, … are called
overtones.
Overtones are often weak
because anharmonicity at
low v is small.

11. Rotation – Vibration Transitions
The rotational selection rule during
a vibrational transition is:
DJ = 1
Unless the molecule has an odd
number of electrons (e.g. NO).
Then,
DJ = 0, 1
    0,1,2..Jand0,1,2,...for11/2E v  vJJBvvJ 
Bv signifies the dependence of B on vibrational level

12. Rotation – Vibration
Transitions
Ingle and Crouch, Spectrochemical Analysis
If DJ = -1  P – Branch
If DJ = 0  Q – Branch
If DJ = +1  R – Branch

13. Thank you