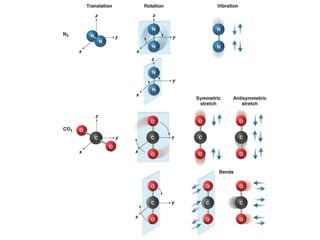
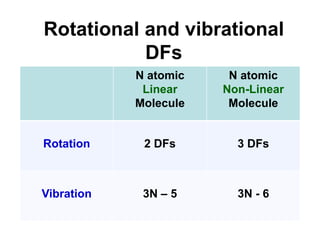
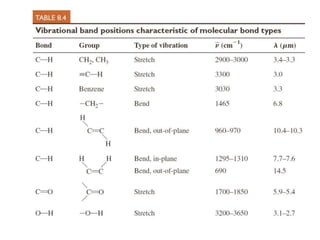
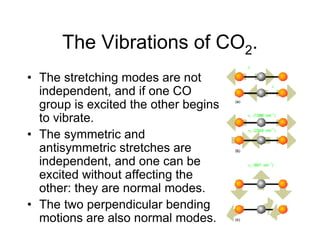
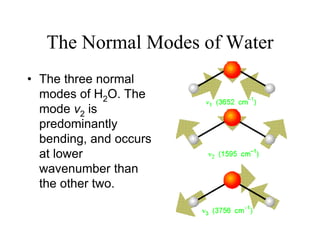
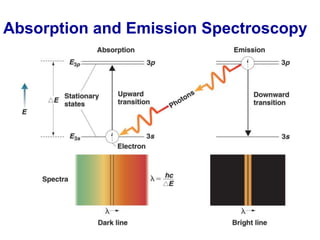
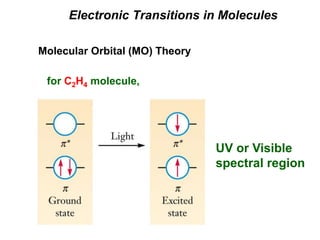
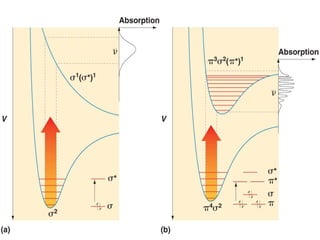
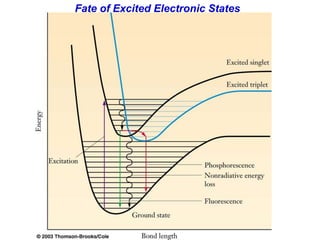
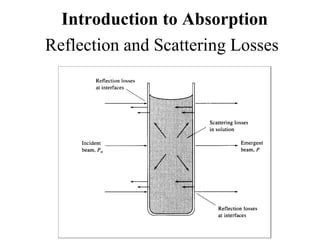
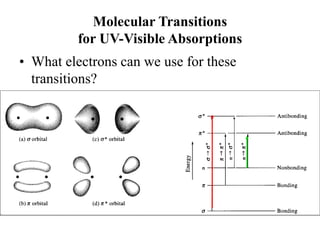
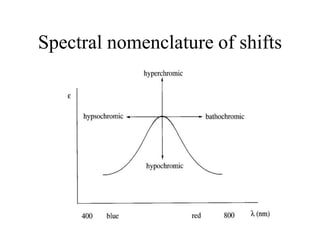
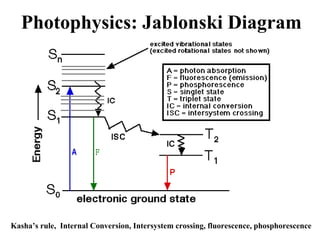
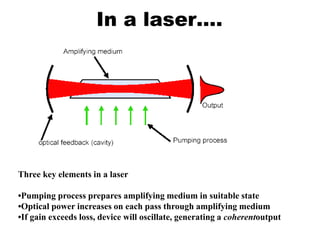
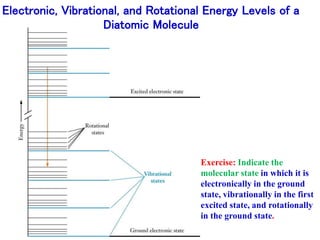
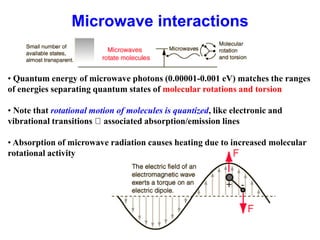
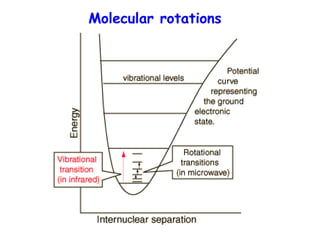
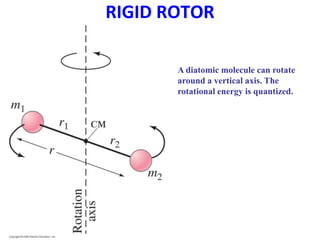
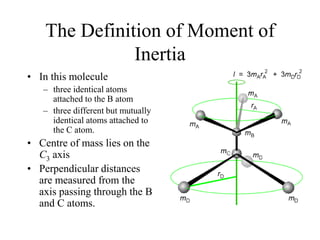
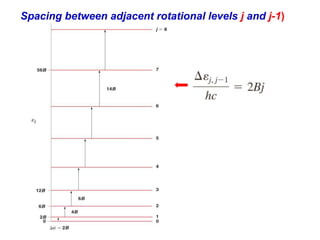
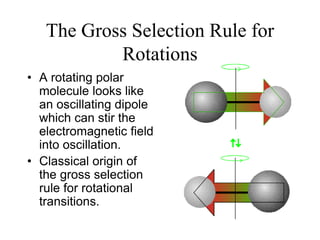
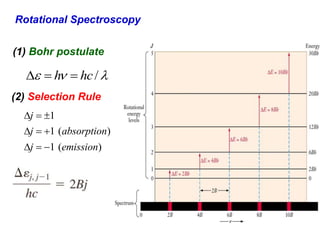
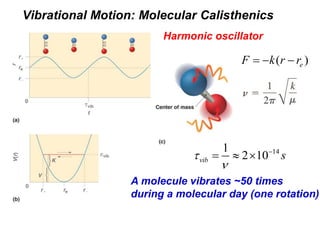
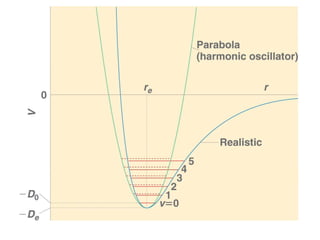
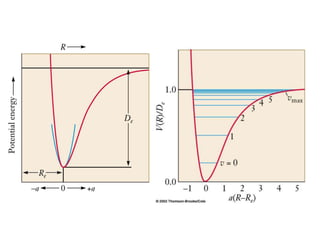
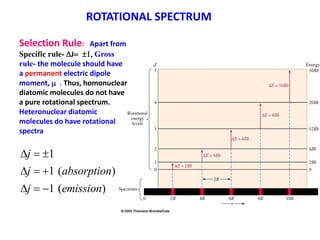
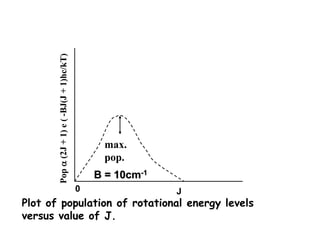
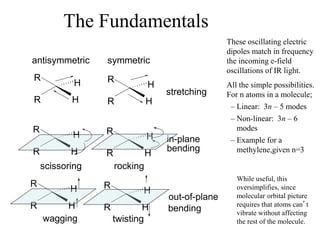
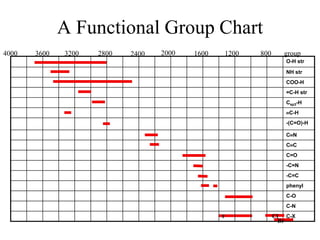
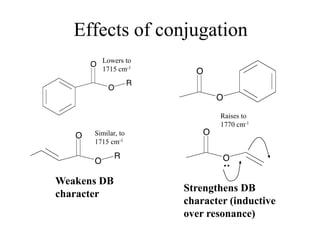
This document provides an overview of molecular spectroscopy techniques, including rotational spectroscopy, vibrational spectroscopy, and absorption and emission spectroscopy. Rotational spectroscopy uses microwave spectroscopy to study the quantized rotational energy levels of molecules. Vibrational spectroscopy uses infrared spectroscopy to analyze the quantized vibrational energy levels of bonds as they stretch, bend, and vibrate. Absorption and emission spectroscopy examines how molecules absorb and emit photons during electronic transitions between energy levels.

1. Degrees of Freedom
Rotational Spectroscopy
Electronic Transitions
Vibrational Spectroscopy
microwave infrared
Interaction with matter Energy levels
Spectroscopy
Absorption Spectroscopy Emission Spectroscopy

2. Introduction to Matters
Rotational Spectroscopy
Vibrational Spectroscopy
Absorption and emission Spectroscopy
Lakowicz, “Principles of Fluorescence Spectroscopy”, Springer Publishers, 3rd Edition, 2011
Atkins, Physical Chemistry, 9th edition, 2009
Banwell & McCash, Fundamentals of Molecular Spectroscopy, 4th edition, 1996
Moog, Spencer and farrell, Physical Chemistry: A Guided Inquiry: Atoms, Molecules,
and Spectroscopy, 2003

3. • The sun produces a full spectrum of electromagnetic
radiation
http://csep10.phys.utk.edu/astr162/lect/light/spectrum.html
http://kr.blog.yahoo.com/bmw26z/2188

4. Components of Electro Magnetic
Radiation
v

5. Two Components of EM
Radiation
• Electrical field (E): varies in magnitude in a direction
perpendicular to the direction of propagation
• Magnetic field (M): at right angle to the electrical
field, is propagated in phase with the electrical field
• Wavelength (l), distance from one wave crest to another
• Frequency (n), No. of crests passing a fixed point/ given time
• Amplitude, height of each peak (watts/sq. meter
• The speed of EM energy “c” 300,000km/second,
c = nl where l and n are inversely related

6. Interaction of radiation with matter
• If there are no available quantized energy levels matching the quantum
energy of the incident radiation, then the material will be transparent to that
radiation
Wavelength

7. Fate of molecule?
• Non-radiative transition: M* + M  M + M + heat
• Spontaneous emission: M*  M + hn (very fast for large
DE)
• Stimulated emission (opposite to stimulated absorption)
These factors contribute to linewidth & to lifetime of excited
state.

8. Molecular Motion and Spectroscopy
Study of Interaction of Matter and Light (Photon)
• Molecular Spectroscopy
 Information about molecules such as geometry and energy
levels are obtained by the interaction of molecules and photons
• Molecular motions: Translation, Rotation, Vibration
 determines the energy levels for the absorption or emission of
photons

9. Electronic, Vibrational, and Rotational Energy Levels of a
Diatomic Molecule
Exercise: Indicate the
molecular state in which it is
electronically in the ground
state, vibrationally in the first
excited state, and rotationally
in the ground state.

10. ROTATIONAL
SPECTROSCOPY

11. Microwave interactions
• Quantum energy of microwave photons (0.00001-0.001 eV) matches the ranges
of energies separating quantum states of molecular rotations and torsion
• Note that rotational motion of molecules is quantized, like electronic and
vibrational transitions associated absorption/emission lines
• Absorption of microwave radiation causes heating due to increased molecular
rotational activity

12. Molecular rotations

13. Types of Rigid Rotors
• A schematic illustration of the
classification of rigid rotors.

14. A diatomic molecule can rotate
around a vertical axis. The
rotational energy is quantized.
RIGID ROTOR
Figure 40-16 goes here.

15. THE RIGID ROTOR
A diatomic molecule may be thought of as two atoms held
together with a massless, rigid rod (rigid rotator model).
o
 r1 | r2 
m1 m2
o
• Consider a diatomic molecule with different atoms of mass
m1 and m2, whose distance from the center of mass are r1 and
r2 respectively
• The moment of inertia of the system about the center of
mass is:
I  m1r1
2
 m2r2
2

16. The Definition of Moment of
Inertia
• In this molecule
– three identical atoms
attached to the B atom
– three different but mutually
identical atoms attached to
the C atom.
• Centre of mass lies on the
C3 axis
• Perpendicular distances
are measured from the
axis passing through the B
and C atoms.

17. Rotational levels
)1(
2
22
2
2
22








JJ
h
L
momentumangularLwhere
I
LI
Er


• The classical expression for energy of rotation is :In the
harmonic oscillator model, the energy was all potential
energy. In the rigid rotor, it’s all kinetic energy:
•
• where J is the rotational quantum number
constantrotationalthe
8
)1()1(
22
1
)(
2
2
Ic
h
B
JJBchJJ
h
I
JE


n
n









18. Quantization of Rotational Energy
2
( )
8
h
B
cI

V = 0
cyclic boundary condition: Ψ(2π + θ) = Ψ(θ)
By solving Schrodinger equation for rotational motion
the rotational energy levels are
Rotational energy levels in wavenumber (cm-1)

19. Spacing between adjacent rotational levels j and j-1)

20. The Gross Selection Rule for
Rotations
• A rotating polar
molecule looks like
an oscillating dipole
which can stir the
electromagnetic field
into oscillation.
• Classical origin of
the gross selection
rule for rotational
transitions.

21. /h hc n lD  
1
1 ( )
1 ( )
j
j absorption
j emission
D  
D  
D  
Rotational Spectroscopy
(1) Bohr postulate
(2) Selection Rule

22. Vibrational Motion: Molecular Calisthenics
Harmonic oscillator
( )eF k r r  
141
2 10vib s
n

  
A molecule vibrates ~50 times
during a molecular day (one rotation)

23. Quantization of Vibrational Energy
By solving Schrodinger equation for vibrational motion,
Vibrational energy level
Zero point energy
Spacing between adjacent vibrational sates
where is a vibrational quantum number

26. ROTATIONAL SPECTRUM
Selection Rule: Apart from
Specific rule- DJ 1, Gross
rule- the molecule should have
a permanent electric dipole
moment, m . Thus, homonuclear
diatomic molecules do not have
a pure rotational spectrum.
Heteronuclear diatomic
molecules do have rotational
spectra
1
1 ( )
1 ( )
j
j absorption
j emission
D  
D  
D  

27. Appearance of rotational spectrum We can calculate
the energy corresponding to rotational transitions
D E=EJ’ –EJ for
Or generally:
J  J + 1 = B(J+1)(J+2) - BJ(J+1)
= 2B(J+1) cm-1
Microwave absorption lines should appear at
J = 0  J = 1 : = 2B - 0 = 2B cm-1
J = 1  J = 2 : = 4B cm-1
Note that the selection rule is DJ = 1, where +
applies to absorption and - to emission.
ν
1D initialfinal JJJ
ν

28. Relative Intensities of rotation spectral
lines
Now we understand the locations (positions)
of lines in the microwave spectrum, we can
see which lines are strongest.
J  BJ(J+1)
J=0  0
Intensity depends upon two factors:

29. Intensity depends upon two factors:
1.Greater initial state population gives stronger spectral
lines.This population depends upon temperature, T.
k = Boltzmann’s constant, 1.380658 x 10-23 J
K-1
(k = R/N)
We conclude that the population is smaller for
higher J states.













kT
νhc
exp
kT
E
exp
N
N J
0
J
cmK1.52034
k
hc







T
ν1.52034
e
N
N
o
J

30. 2. Intensity also depends on degeneracy of initial
state.
(degeneracy = existence of 2 or more energy states having exactly
the same energy)
Each level J is (2J+1) degenerate
 population is greater for higher J states.
To summarize: Total relative population at energy
EJ  (2J+1) exp (-EJ / kT) & maximum population
occurs at nearest integral J value to :
Look at the values of NJ/N0 in the figure, .

31. Plot of population of rotational energy levels
versus value of J.
B = 10cm-1
max.
pop.
J0
Pop(2J+1)e(-BJ(J+1)hc/kT)

32. MCWE or Rotational Spectroscopy
Classification of molecules
• Based on moments of inertia, I=mr2
– IA  IB  IC very complex eg H2O
– IA = IB = IC no MCWE spectrum
eg CH4
– IA  IB = IC complicated eg NH3
– IA = 0, IB = IC linear molecules eg NaCl
 
E
J J
I
J M JJ J

   
1
2
012 0 1
2

 with also, , , , ,

33. Vibrational Spectroscopy

34. Vibrational Spectra
Molecules are not Static
Vibration of bonds occurs in the liquid, solid and gaseous phase
Vibrating  Energy  Frequency (and the appropriate frequencies
for molecular vibrations are in the Infrared region of the
electromagnetic spectrum
Vibrations form therefore, a fundamental basis for spectroscopy in
chemistry--the bonds are what makes the chemistry work in structure
and function
For Organic Chemistry the most important uses of these vibrations is
for analysis of:
•functional groups
•structural identity, “fingerprinting”

35. What Kind of vibrations are These?
Bonds can…….
Stretch
Bend
Wag
(rock)
These can number into the
hundreds.
Some are symmetrical, some
antisymmetrical and many are
coupled across the molecule
Can be calculated. One easy
approximation is:
m
n
k12
103.5 -
´=
21
21
mm
mm
+
=m The “reduced mass” where m1, m2
are the masses on either side of
vibration
k is the “force constant”, like the
Hookes Law restoring force for a
spring. Known and tabulated for
different vibrations

36. The Fundamentals
R
R
H
H
R
R
H
H
R
R
H
H
R
R
H
H
R
R
H
H
R
R
H
H
antisymmetric symmetric
rockingscissoring
in-plane
bending
stretching
out-of-plane
bending
wagging twisting
These oscillating electric
dipoles match in frequency
the incoming e-field
oscillations of IR light.
All the simple possibilities.
For n atoms in a molecule;
– Linear: 3n – 5 modes
– Non-linear: 3n – 6
modes
– Example for a
methylene,given n=3
While useful, this
oversimplifies, since
molecular orbital picture
requires that atoms can’t
vibrate without affecting
the rest of the molecule.

37. A Functional Group Chart
O-H str
NH str
COO-H
=C-H str
Csp3-H
C-H
-(C=O)-H
CN
CC
C=O
-C=N
-C=C
phenyl
C-O
C-N
F C-X
4000 3600 3200 2800 2400 2000 1600 1200 800 group
Br
Cl

38. Regions of Frequencies
Near -to
visible- IR
(NIR)
Combination
bands
3.8 x 1014 to 1.2
x 1014
12800 to 4000 0.78 to 2.5
Mid Infrared
Fundmental
bands for
organic
molecules
1.2 x 1014 to 6.0
x 1012
4000 to 200 2.5 to 50
Far IR
Inorganics
organometallics
6.0 x 1012 to 3.0
x 1011
200 to 10 50 to 1000
Spectral Region Frequency(Hz) Wavenumber(cm-1) Wavelength (l,mm)

39. Looking at a Spectrum
Divide the spectrum in to two regions:
4000 cm-1 1600 cm-1 most of the stretching bands,
specific functional groups
(specific atom pairs). This is the
“functional group” region.
1600 cm-1  400 cm-1 Many band of mixed origin. Some
prominent bands are reliable. This
is the “fingerprint” region. Use
for comparison with literature
spectra.
Wavenumber is cm-1=104/l(m)

40. What kinds of Bonds Absorb in
which Regions?
Bending is easier than stretching-- happens at lower energy
(lower wavenumber)
Bond Order is reflected in ordering-- triple>double>single (energy)
with single bonds easier than double
easier than triple
Heavier atoms move slower than
lighter ones
The k in the frequency
equation is in mDyne/Å of
displacement
Single bond str 3-6 mD/Å
Double bond str. 10-12 mD/Å
Triple Bond 15-18 mD/Å

41. Effects of conjugation
Lowers to
1715 cm-1
Similar, to
1715 cm-1
Raises to
1770 cm-1
:
Weakens DB
character
Strengthens DB
character (inductive
over resonance)

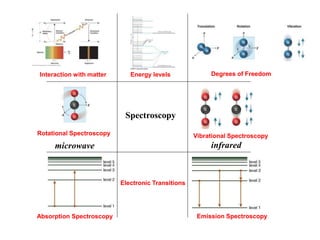
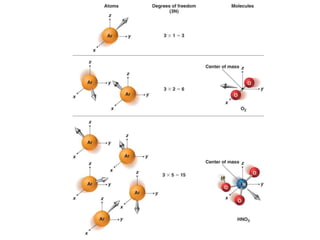
42. Degrees of Freedom:
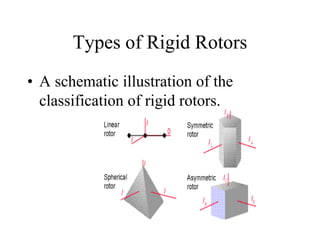
Translation, Rotation, and Vibration
Consider a single Ar atom moving in 3-D space:
- Moving motion is referred to as Translation
- To analyze the translation of an Ar, we need to know
position (x, y, z) and momentum (px, py, pz)
Where it is Where it is headed
- Each coordinate-momentum pair [for example, (x,px)] is
referred to as a Degree of Freedom (DF)
- An Ar atom moving through 3-D space has three DFs
N argon atoms possesses 3N DFs:
All translational DFs

45. Center of Mass (Balanced
Point)
- A point mass that can represent the
molecule
- Motion of the center of mass requires 3 DFs
to describe it
- In general, regardless of its size or
complexity, a molecule has 3 translational
DFs
- Thus, (3N – 3) DFs for the internal motions
of rotation and vibration

46. Rotational and vibrational
DFs
N atomic
Linear
Molecule
N atomic
Non-Linear
Molecule
Rotation 2 DFs 3 DFs
Vibration 3N – 5 3N - 6

47. Vibrational Spectroscopy
Vibrational selection rule
1
1 ( )
1 ( )
absorption
emission



D  
D  
D  

49. The Vibrations of CO2.
• The stretching modes are not
independent, and if one CO
group is excited the other begins
to vibrate.
• The symmetric and
antisymmetric stretches are
independent, and one can be
excited without affecting the
other: they are normal modes.
• The two perpendicular bending
motions are also normal modes.

50. The Normal Modes of Water
• The three normal
modes of H2O. The
mode v2 is
predominantly
bending, and occurs
at lower
wavenumber than
the other two.

51. Absorption and Emission Spectroscopy

52. Electronic Transitions in Molecules
Molecular Orbital (MO) Theory
for C2H4 molecule,
UV or Visible
spectral region

54. Department of Chemistry, KAIST
Fate of Excited Electronic States

55. Reflection and Scattering Losses
Introduction to Absorption

56. LAMBERT-BEER LAW
ionconcentrat
pathlength
tyabsorptivi
loglog
0
0












c
b
a
kcabcA
P
P
TA
P
P
P
P
T
solvent
solution
Power of
radiation after
passing through
the solvent
Power of radiation
after passing
through the sample
solution

57. Beer’s law and mixtures
• Each analyte present in the solution absorbs light!
• The magnitude of the absorption depends on its 
• A total = A1+A2+…+An
• A total = 1bc1+2bc2+…+nbcn
• If 1 = 2 = n then simultaneous determination is
impossible
• Need nl’s where ’s are different to solve the mixture

58. Molecular Transitions
for UV-Visible Absorptions
• What electrons can we use for these
transitions?

59. Spectral nomenclature of shifts

60. Introduction to Emission
• Luminescence: emission of photons from
electronically excited states of atoms,
molecules, and ions.
• Fluorescence: Average lifetime from <10—10
to 10—7 sec from singlet states.
• Phosphorescence: Average lifetime from 10—5
to >10+3 sec from triplet excited states.

61. Importance of Emission
Spectroscopy
• Sensitivity to local electrical environment
– polarity, hydrophobicity
• Track (bio-)chemical reactions
• Measure local friction (microviscosity)
• Track solvation dynamics
• Measure distances using molecular rulers:
fluorescence resonance energy transfer (FRET)

62. Photophysics: Jablonski Diagram
Kasha’s rule, Internal Conversion, Intersystem crossing, fluorescence, phosphorescence

63. Principles
• Interaction of photons with molecules
results in promotion of valence electrons
from ground state orbitals to high energy
levels.
• The molecules are said to be in excited
state.
• Molecules in excited state do not remain
there long but spontaneously relax to more
stable ground state.

64. • The relaxation process is brought about by
collisional energy transfer to solvent or
other molecules in the solution.
• Some excited molecules however return to
the ground state by emitting the excess
energy as light.
• This process is called fluorescence.

65. Light Amplification by Stimulated Emission of Radiation

66. In a laser….
Three key elements in a laser
•Pumping process prepares amplifying medium in suitable state
•Optical power increases on each pass through amplifying medium
•If gain exceeds loss, device will oscillate, generating a coherentoutput