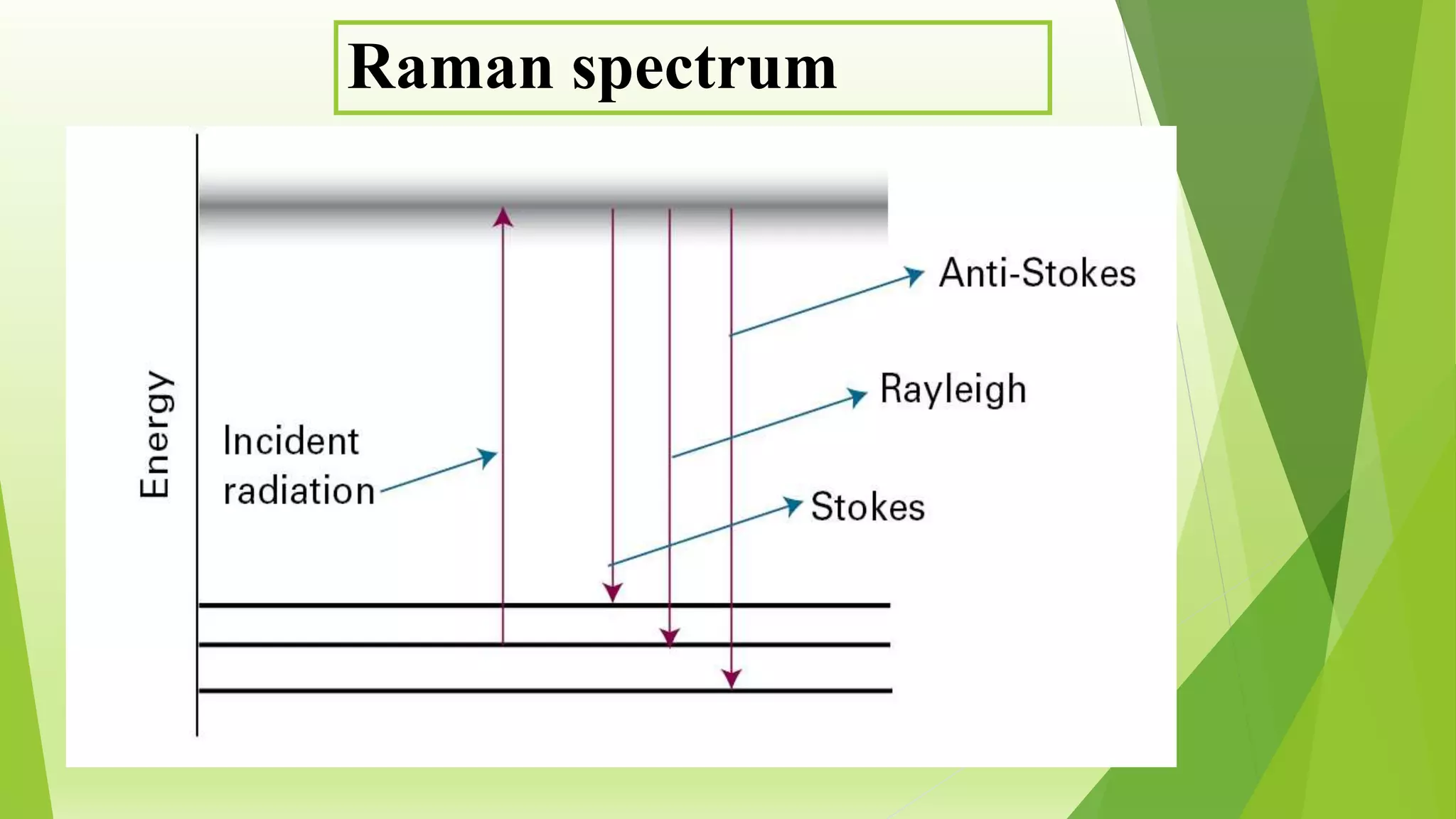
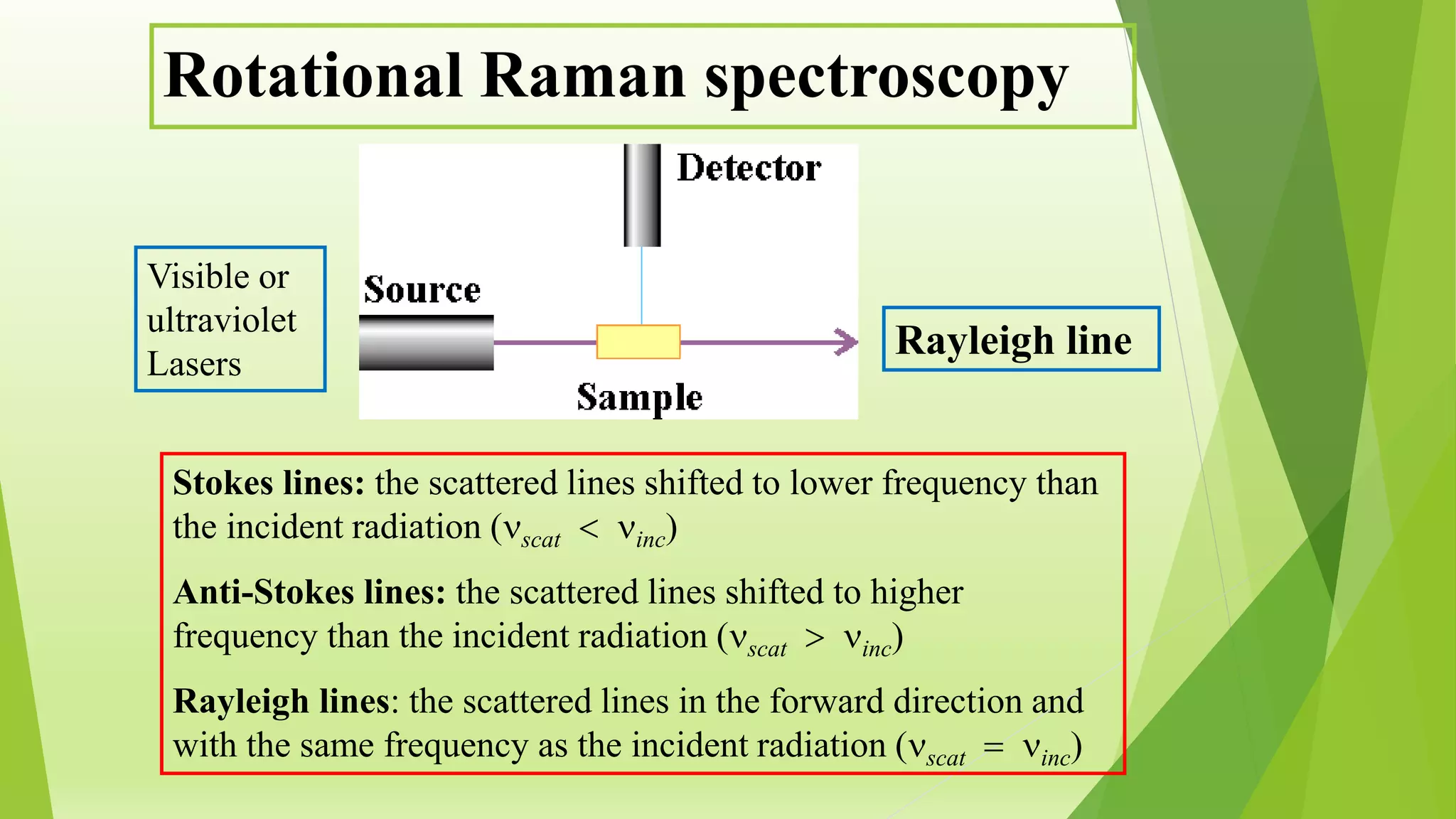
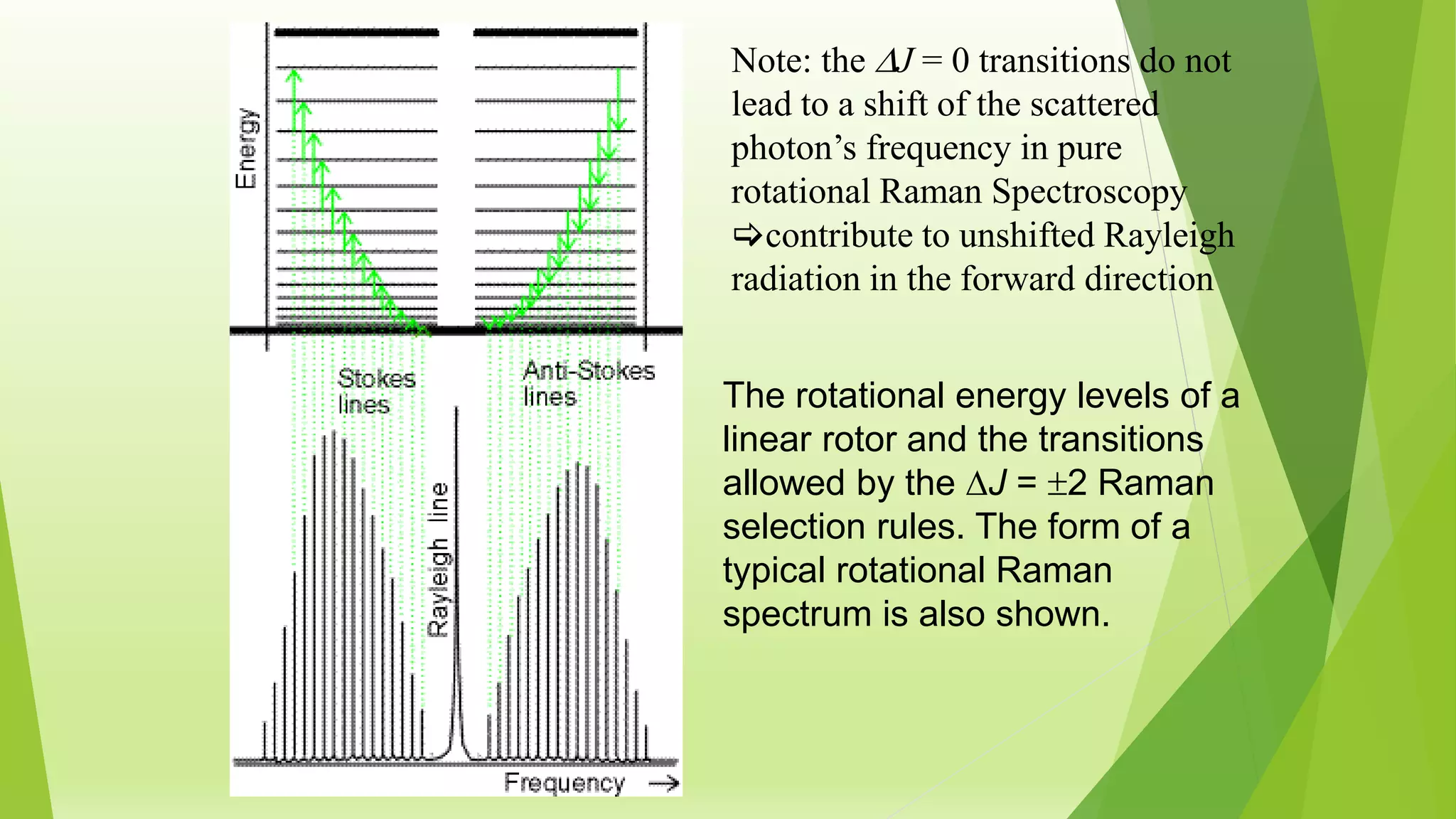
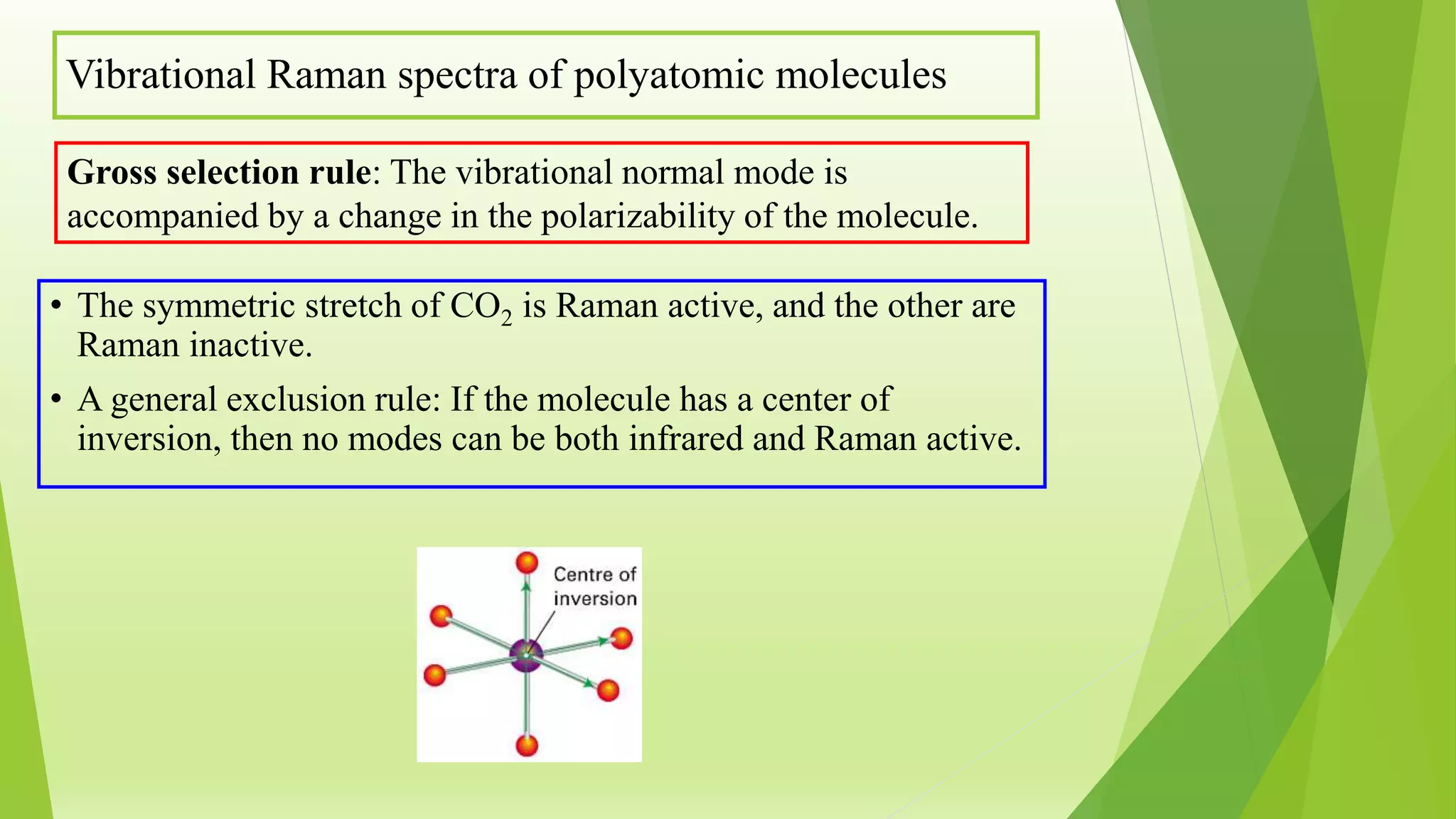
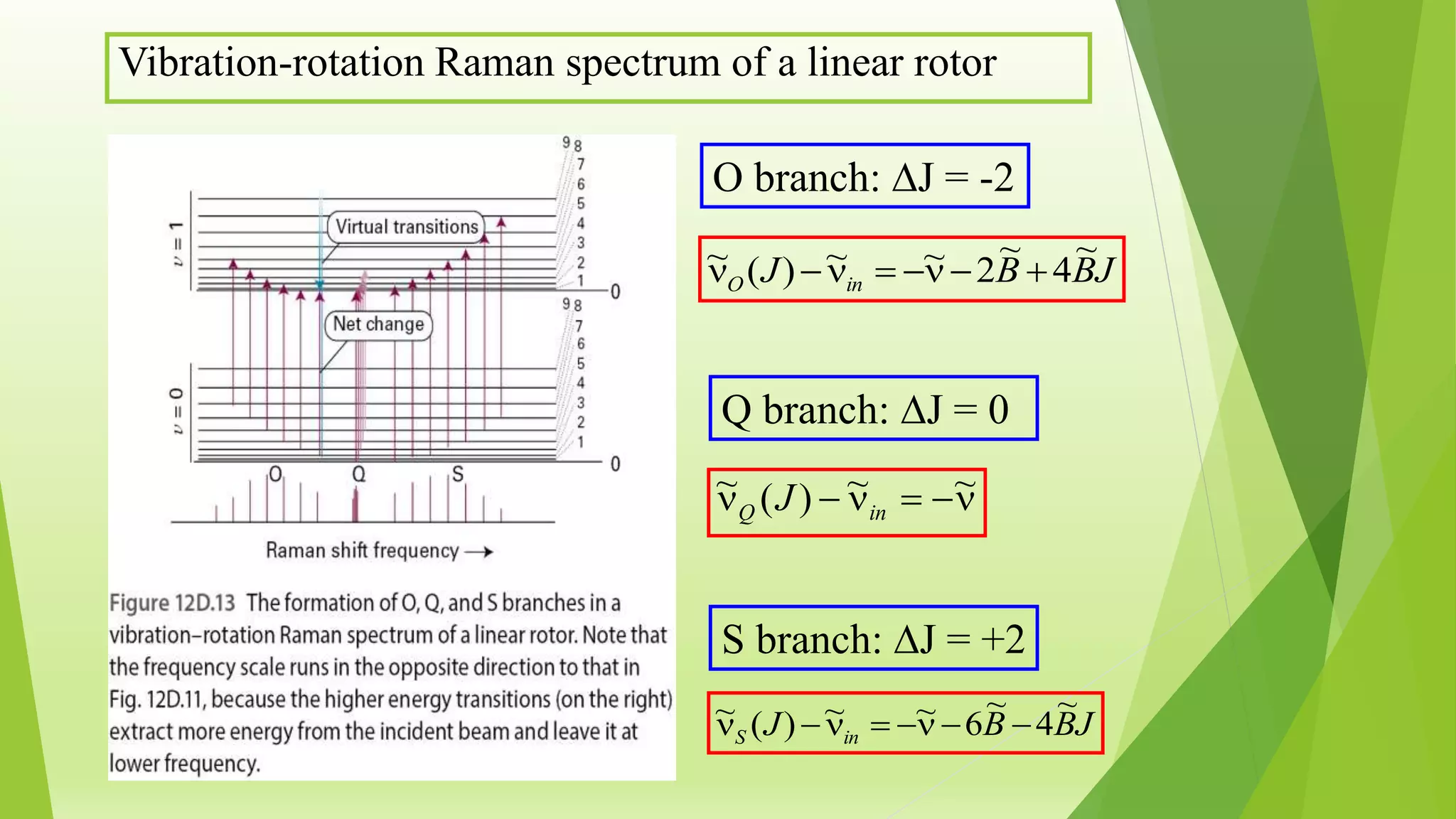
Raman spectroscopy analyzes the scattering of monochromatic light when it interacts with molecular vibrations or rotations. It can provide information about molecular structure. When light interacts with a molecule, the light may be scattered at the same frequency (Rayleigh scattering) or at a shifted lower (Stokes) or higher (anti-Stokes) frequency, depending on whether the molecule gains or loses vibrational or rotational energy. Selection rules determine which molecular motions are observable by Raman spectroscopy. Rotational Raman spectra of linear molecules exhibit a characteristic pattern depending on the change in rotational quantum number.

2. RAMAN SPECTROSCOPY
PURE ROTATIONAL,
VIBRATIONAL,
VIBRATIONAL-ROTATIONAL,
RAMAN SPECTRA.

3. Spectroscopy
 Photons of the radiation bring information to us about the atom, molecule or
matter.
 The different he analysis of the EM radiations emitted, absorbed or scattered
by atoms, molecules or matter
 see between molecular and atomic spectroscopy: a molecule can make a
transition between its electronic, rotational and vibrational states.
 The rotational and vibrational spectroscopy of a molecule can provide
information about the bond lengths, bond angles and bond strength in the
molecule

4. General features of spectroscopy
Emission spectrum: A molecule returns to a state of lower energy
E1 from an excited state of energy E2 by emitting a photon.
Absorption spectrum: A molecule is excited from a lower energy
state to a higher energy state by absorbing a photon as the
frequency of the incident radiation is swept over a range
c
E
E
h








1
~
|
| 2
1
is called the wavenumber of the
photon and gives the number of
complete wavelengths per centimeter.
It is in the unit of cm-1.

~

5. Raman spectrometer
Near IR(780 to 2500 nm)

6. Raman spectrum

7.  Other incident photons may collect energy from excited sample
molecules, emerging as higher frequency anti-Stokes lines.
Raman Spectroscopy
• Molecular energy levels are explored by examining the
frequencies present in radiation scattered by molecules.
• Most of the radiation is scattered without change of
frequency, giving the Rayleigh line.
• About 1 in 107 of the incident photons give up some
energy in collision with the sample molecules,
emerging with lower energy, giving lower frequency
Stokes lines.

8. Rotational Raman spectroscopy
Stokes lines: the scattered lines shifted to lower frequency than
the incident radiation (scat < inc)
Anti-Stokes lines: the scattered lines shifted to higher
frequency than the incident radiation (scat > inc)
Rayleigh lines: the scattered lines in the forward direction and
with the same frequency as the incident radiation (scat  inc)
Rayleigh line
Visible or
ultraviolet
Lasers

9. Rotational Raman Spectra
Gross selection rule for rotational Raman transitions: molecule must
be anisotropically polarizable
An electric field applied to a
molecule results in its distortion,
and the distorted molecule acquires
a contribution to its dipole moment
(even if it is nonpolar initially). The
polarizability may be different when
the field is applied (a) parallel or (b)
perpendicular to the molecular axis
(or, in general, in different
directions relative to the molecule);
if that is so, then the molecule has
an anisotropic polarizability.

10. The distortion of a molecule in an electric field is determined
by its polarizability .
In addition to any permanent dipole moment a molecule may
have, the molecule acquires an induced dipole moment , if
the strength of the field is :
An atom is isotropically polarizable.
All linear molecules and diatomics (whether homonuclear or
heteronuclear) have anisotropic polarizabilities rotationally
Raman active
 allows study of many molecules that are inaccessible to
microwave spectroscopy.
but some types of rotors both rotationally Raman &
microwave inactive

11. Gross selection rule
• The molecules must have anisotropic polarizability.
The polarizability of a molecule is a measure of the extent to which an
applied electric field can induce an electric dipole moment  in addition to
any permanent dipole moment. The anisotropy of the polarizability is its
variation with the orientation of the molecule.
All spherical rotors, like tretrahedral (CH4), octahedral (SF6) and icosahedral
molecules (C60), are both rotationally and rotationally Raman inactive.
All homonuclear diatomic molecules and linear molecules are rotationally
inactive but rotationally Raman active.


>
||

12. Specific rotational Raman selection rules:
Linear rotors: J = 0,  2
The distortion induced in
a molecule by an applied
electric field returns to its
initial value after a
rotation of only 180
(that is, twice a
revolution). This is the
origin of the J = 2
selection rule in
rotational Raman
spectroscopy.

13. Specific rotational Raman
selection rules
Linear rotors: J = 0,  2
Symmetric rotors: J = 0,  1,  2; K = 0
Asymmetric rotors:
For the latter, K is not a good quantum number,
so additional selection rules become too
complex.
A good quantum number is one which is
conserved in the presence of an external
interaction.

14. The rotational energy levels of a
linear rotor and the transitions
allowed by the J = 2 Raman
selection rules. The form of a
typical rotational Raman
spectrum is also shown.
Note: the J = 0 transitions do not
lead to a shift of the scattered
photon’s frequency in pure
rotational Raman Spectroscopy
contribute to unshifted Rayleigh
radiation in the forward direction

15. Stokes and anti-Stokes lines of rotational Raman spectrum
,..
,
,
,
J
J
B
J
B
hc
E
E
E J
J
3
2
1
0
,
)
3
2
(
~
2
)
3
2
(
~
2
)
( 2












 
For Stokes lines (J= +2)
• The rotational Raman spectrum consists of a series of lines at frequencies of
6 , 10 and 14 … , which are separated by 4 .
• We can use the value of B obtained from the rotational Raman spectrum to
estimate the bond length of a homonuclear diatomic molecule.
• The intensities of the Stokes lines are generally stronger than those of the
Anti-Stokes lines.
Stokes lines Anti-Stokes lines
For anti-Stokes lines (J= -2)
,..
,
J
J
B
J
B
hc
E
E
E J
J
3
2
,
)
1
2
(
~
2
)
1
2
(
~
2
2









 
 : Frequency shift relative to the incident radiation.
B
~
B
~
B
~
B
~

16. Rotational Raman spectrum of a diatomic
molecule with two identical nuclei of spin
½
For H2 molecules with nonzero nuclear spins,
the intensities of the odd-J lines are three
times more than those of the even-J lines.
Under rotation through 180°,
Wavefunctions with even J do not change sign.
Wavefunctions with odd J do change sign.
Nuclear statistics must be taken into
account whenever a rotation
interchanges equivalent nuclei.
rot
nuc
total ψ
ψ
ψ 

17. Vibrational Raman spectroscopy
• The incident photon leaves some of its energy in the vibrational modes of
the molecule it strikes (Stokes lines), or collects additional energy from a
vibration that has already been excited (Anti-Stokes lines).
• Gross selection rule: The molecular polarizability must change as the
molecule vibrates.
Both homonuclear and heteronuclear diatomic molecules are vibrationally
Raman active.
• Specific selection rules:
• The Stokes lines are more intense than the Anti-Stokes lines, because very
few molecules are in an excited vibrational state initially.
J = 0 or ±2, n =  1 )
(
)
(
)
( t
E
x
x
in






Induced dipole moment

18. Vibrational Raman spectra of polyatomic molecules
• The symmetric stretch of CO2 is Raman active, and the other are
Raman inactive.
• A general exclusion rule: If the molecule has a center of
inversion, then no modes can be both infrared and Raman active.
Gross selection rule: The vibrational normal mode is
accompanied by a change in the polarizability of the molecule.

19. Features of normal modes
A vibrational normal mode describes
a specific collective motion of atoms,
with each atom in a harmonic
oscillation of the same frequency. The
collective motion of a normal mode is
called a vibrational excitation.
In the harmonic approximation, all
normal modes of a molecule are
independent from one another. Each
normal mode behaves like an
independent harmonic oscillator. The
energies of the vibrational levels of
the i-th normal mode with frequency
i are

i
i
n h
n
E i









2
1
Symmetric atretching and antisymmetric
stretching modes of CO2 molecule
Antisymmetric
stretching mode
Symmetric
Stretching mode

20. Vibration-rotation Raman spectrum of a linear rotor
Q branch: J = 0
S branch: J = +2
O branch: J = -2
J
B
B
J in
O
~
4
~
2
~
~
)
(
~ 












 ~
~
)
(
~
in
Q J
J
B
B
J in
S
~
4
~
6
~
~
)
(
~ 








21. Vibration-rotation Raman spectrum of CO
J=+2
J=-2 J=0

22. “
”