This document covers key concepts in analyzing multiple random variables, including:
- Joint distributions and independence of multiple random variables
- Moment generating functions and their use in determining distributions and moments
- Properties of sums and transformations of random vectors
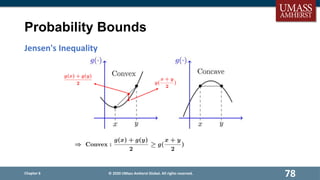
- Common probability inequalities like union bound, Markov's inequality, and Chernoff bounds