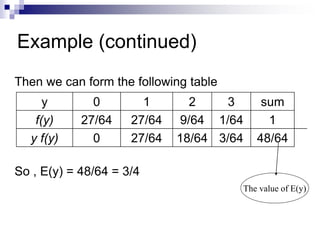
The document discusses expectation of discrete random variables. It defines expectation as the weighted average of all possible values a random variable can take, with weights given by each value's probability. Expectation provides a measure of the central tendency of a probability distribution. Several examples are provided to demonstrate calculating expectation for different discrete random variables and distributions like binomial, geometric, and Poisson. Properties of expectation like linearity and independence are also covered.

1. Expectation of Discrete
Random Variable
• Student : Alyasar Jabbarli
• Group: 652.20ES
• İnstructor : Rugiyya Azizova

2. Expectation of Discrete Random
Variable
One of the important concept in probability theory is that of the
expectation of a random variable. The expected value of a random
variable X, denoted by E(X) or , measure where the
Probability distribution is centered.
Definition :
Let X be a discrete random variable having a probability mass
Function f(x). If
Then , the expected value (or mean) of X exist and is define as
x

 

x
x
f
x )
(


x
x
xf
X
E )
(
)
(

3. Expectation of Discrete Random
Variable
In words , the expected value of X is the weighted
average of the possible values of X can take on , each
value being weighted by the probability that X assumes it.

4. Example
The probability mass function of the random
variable X is given by
Find the expected value of X.
x 1 2 3
x f (x) 1/2 1/3 1/6

5. Solution:
Then ,
= 10/6
x 1 2 3 sum
f(x) 1/2 1/3 1/6 1
x f(x) 1/2 2/3 3/6 106


x
x
xf
X
E )
(
)
(
The value of E(x)

6. Example
The probability distribution of the discrete random variable Y is
Find the mean of Y.
Solution:
Get the values of f(y) such as
When y=0 then
When y=1 then
And so on then
3
,
2
,
1
,
0
4
3
4
1
3
)
(
3























y
y
y
f
y
y
64
/
27
4
3
4
1
0
3
)
0
(
0
3
0























f
64
/
27
4
3
4
1
1
3
)
1
(
1
3
1























f

7. Example (continued)
y 0 1 2 3 sum
f(y) 27/64 27/64 9/64 1/64 1
y f(y) 0 27/64 18/64 3/64 48/64
Then we can form the following table
So , E(y) = 48/64 = 3/4
The value of E(y)

8. Example
A pair of fair dice is tossed. Let X assign to each point
(a,b) in S the maximum of its number, i.e.
X (a,b) = max (a, b) . Find the probability mass function
of X , and the mean of X .
Solution: When toss a pair of fair dice
S={(1,1),(1,2),(1,3)……………..(6,5),(6,6)}
E(x) = 161/36
x 1 2 3 sum
f(x) 1/2 1/3 1/6 1
x f(x) 1/2 2/3 3/6 106
E(x)

9. Example
Find the expected number of chemists on committee of 3
selected at random from 4 chemists and 3 biologists .
Solution:
Now we want to form the table of function
1- get the value of X = the number of chemist in the committee
x = 0,1,2,3
2- get the values of mass functions f(x)
x=0 , then f(0)=P(X=0) =
x=2 , then f(2)=P(X=2) =
35
1
3
7
3
3
0
4

























X=no. of chemist
35
18
3
7
1
3
2
4


























10. Example
E(X) = 60/35 =1.7
Note:
E(X) need not be an integer .
x 0 1 2 3 sum
f(x) 1/35 12/35 18/35 4/35 1
x f(x) 0 12/35 36/35 12/36 60/35
E(x)

11. Example
Let X be the following probability mass function
Find E(X3(
Solution:
= 1/6+16/6+81/6=98/6







elsewhere
x
x
x
f
.
..........
0
3
,
2
,
1
..........
6
)
(


x
x
f
X
X
E )
(
)
( 3
3

12. Expected value(mean) of some
distributions
x
Distribution E(X)= mean
Binomail dist. E(X) = np
Hypergeometric E(X) = n M / N
Geometric dist. E(X)= 1/ P
Poisson dist. E(X) = ‫ג‬
Uniform dist. E(X) = (N+1)/ 2

13. Examples
Example 1:
A fair die is tossed 1620 times. Find the expected number
of times the face 6 occurs.
Solution:
X= # of times faces {6} occurs
X ~Bin(1620,1/6) ,then
E(X) = np = 1620 * 1/6 = 270
Example 2:
If the probability of engine malfunction during any 1-hour
period is p=0.02 and X is the number of 1-hour interval
until the first malfunction , find the mean of X.
Solution:
X ~g(0.02) ,then
E(X) = 1/P= 1/0.02=50

14. Example 3:
A coin is biased so that a head is three times as likely to
occur as a tail. Find the expected number of tails when this
coin is tossed twice.
Solution:
Since coin is biased then
P(H) = 3 P(T) [ since P(H)+P(T) = 1
3P(T)+P(T)=1 4P(T)=1 P(T)= ¼ ]
X= # of tails (T)
X ~Bin(2,1/4) ,then
E(X) = np = 2 *1/4 = 1/2

15. Example 4:
If X has a Poisson distribution with mean 3 . Find
the expected value of X.
Solution :
X ~Poisson(3)
then
E(x) = ‫ג‬ = 3

16. Properties of Expectation:
1.If X is a random variable with probability distribution f(x).The mean or
expected value of the random variable g(x) is
(Law of unconscious statistician)
2. If a and b are constants ,then
(I) E(a) = a
(II) E(aX) = a E(X)
(III) E(aX ± b) =E(aX) ± E(b) = a E(X) ± b
(IV)


x
x
f
x
g
x
g
E )
(
)
(
))
(
(


x
x
f
x
X
E )
(
)
( 2
2

17. Example
If X is the number of points rolled with a balanced die,find the
expected value of the random variable g(x)= 2 X2
+1
Solution:
S={1,2,3,4,5,6} each with probability 1/6
E(g(x))=E(2 X2
+1)=2E(X2
)+E(1)
=2 * 91/6 + 1=188/6=31.3
x 1 2 3 4 5 6 sum
f(x) 1/6 1/6 1/6 1/6 1/6 1/6 1
xf(x) 1/6 2/6 3/6 4/6 5/6 6/6 21/6
x2
f(x) 1/6 4/6 9/6 16/6 25/6 36/6 91/6

18. Expectation and moments for Bivariate
Distribution
We shall now extend our concept of mathematical expectation to the
case of n random variable X1 , X2 ,….,Xn with joint probability
distribution f(x1 , x2 ,….,xn ).
Definition:
Let X1 , X2 ,….,Xn be a discrete random vector with joint probability
distribution f(x1 , x2 ,….,xn ) and let g be a real valued function.
Then the random variable Z=g(x1 , x2 ,….,xn )expectation has finite
expectation if and only if


 )
,...
,
(
)
,...
,
( 2
1
,...
,
2
1
2
1
n
x
x
x
n x
x
x
f
x
x
x
g
n

19. and in this case the expected value of Z, denoted by
Example:
Let X and Y be the random variable with the following joint
probability function.
Find the expected value of
g(x,y)= XY
Solution:
=0*0*f(0,0)+0*1*f(0,1)+…+1*1*f(1,1)+…+2*0*f(2,0)
=f(1,1) =3/4
)
,...
,
(
)
,...
,
(
))
,...
,
(
( 2
1
,...
,
2
1
2
1
2
1
n
x
x
x
n
n x
x
x
f
x
x
x
g
x
x
x
g
E
n


y/x 0 1 2
0 3/28 9/28 3/28
1 3/14 3/14 0
2 1/28 0 0

 

2
0
2
0
)
,
(
)
(
x x
y
x
xyf
x
E

20. Theorem 1:
The expected value of the sum or difference of two or more functions of
the random variables X,Y is the sum or difference of the expected values
of the function. That is
Generalized of the above theorem to n random variables is straightforward.
Corollary:
Setting g(x,y)=g(x) and h(x,y)=h(y),we see that
Corollary:
Setting g(x,y)= x and h(x,y)=y ,we see that
And in general
)]
,
(
[
)]
,
(
[
)]
,
(
)
,
(
[ Y
X
h
E
Y
X
g
E
Y
X
h
Y
X
g
E 


)]
(
[
)]
(
[
)]
(
)
(
[ Y
h
E
X
g
E
Y
h
X
g
E 


]
[
]
[
]
[ Y
E
X
E
Y
X
E 



 


n
i
i
n
i
i X
E
X
E
1
1
)
(
)
(

21. Theorem 2: (Independence)
If X and Y are two independent random variables having
finite expectations. Then XY has finite expectation and
E(XY) = E(X)E(Y)
Note: opposite are not true
If E(XY) = E(X)E(Y) X,Y independent
In general, if X1, X2 ,….., Xn are n independent random
variables such that each expectation E(Xi) exists
(i=1,2,…n(, then
)
(
)
(
1
1

 


n
i
i
n
i
i X
E
X
E

22. Example1 :
Let (X,Y) assume the values (1,0),(0,1),(-1,0),(0,-1) with
equal probabilities. Show that the equation satisfied
E(XY) = E(X)E(Y)
Solution:
However, the random
Variables X and Y are
not independent
Then,
x
Y
-1 0 1 sum
-1
0
1
sum
0
1/4
1/4
1/4
1/4
0
0
0
0
2/4
1/4
1/4
1
1/4 1/4
2/4
Prob.= 1/n=1/4
f(y)
f(x)

23. Example
E (X)= -1x1/4+0x2/4+1x1/4=-1/4+0+1/4=0
E (Y)= -1x1/4+0x2/4+1x1/4=-1/4+0+1/4=0
E(X) E(Y) = 0
Now,
E(XY) = (-1x -1x0) + (-1x0x1/4)+…..+(1x0x1/4)+(1x1x0)
= 0 + 0 +……..+ 0 + 0 = 0
Then, E(XY) = E(X)E(Y)
0 = 0 (equation is satisfied)
However, X and y are not independent since
4
2
4
2
0
)
0
(
)
0
(
)
0
,
0
(


 y
x f
f
f

24. Example
Suppose that X1, X2 and X3 are independent random
variables such that E(Xi)=0 and E(Xi
2(=1 for i=1,2,3
Find E(X1
2 (X2 - 4 X3 (2 (
Solution:
Since X1, X2 and X3 are independent
X1
2 and (X2 - 4 X3 (2 are also independent
E(X1
2 (X2 - 4 X3 (2 (=E(X1
2)E( X2 - 4 X3 (2
= 1x E(X2
2- 8X2 X3 + 16 X3
2 (
=E(X2
2( - 8E(X2 X3( + 16 E(X3
2 (
=1-8 E(X2)E(X3) + 16x 1
= 1-(8x0x0) + 16=17
Remember if X,Y indep,then
E(X)E(Y)
E(XY) 

25. Conditional Expectation
Definition: Let X and Y be two random variables with joint probability
Distribution f(x,y). The conditional expectation of X, given Y=y, is defined
as
Where f(xy) is the conditional distribution of X given Y = y



x
y
x
xf
y
Y
X
E )
(
)
|
(
)
(
)
,
(
)
(
y
f
y
x
f
y
x
f
y


26. Example
If the joint probability distribution function of X and Y are as shown in
The following table:
Find:
1.The conditional distribution of X given
Y= -1, That is [f(xy= -1) for every x]
When X= -1
When X = 1
y x -1 1 sum
-1 1/8 1/2 5/8
0 0 1/4 1/4
1 1/8 0 1/8
sum 2/8 3/4 1
8
/
5
)
1
,
(
)
1
(
)
,
(
)
1
(






x
f
f
y
x
f
y
x
f
y
5
/
1
8
/
5
8
/
1
8
/
5
)
1
,
1
(
)
1
( 






f
y
x
f
5
/
4
8
/
5
2
/
1
8
/
5
)
1
,
1
(
)
1
( 





f
y
x
f
x -1 1
f(x/y=-1) 1/5 4/5

27. Example
2. The conditional mean of X given Y= -1
x -1 1 sum
f(x/y=-1) 1/5 4/5 1
xf(x/y=-1) -1/5 4/5 3/5
5
/
3
)
(
)
|
( 

 
x
y
x
xf
y
Y
X
E

28. Variance
The variance measures the degree to which a distribution is
concentrated
around its mean. Such measure is called the variance (or dispersion).
Definition:
The variance of a random variable X, denoted by Var(X) or σx
2 where
In other words,
Since the variance is the expected value of the nonnegative random
variable (X-μx
2(,then it has some properties.
2
2
2
))
(
(
)
(
)
( X
E
X
E
X
E
X
Var x
x 



 

2
2
2
2
2
))
(
(
)
(
)
(
)
( X
E
X
E
X
E
X
Var x
x 



 


29. Properties of variance:
1. Var(X(≥0
2. Is called the standard deviation of X.
3. The variance a distribution provides a measure of the
spread or dispersion of the distribution around its mean
μx.
4. If a, b are constants , then
(i) Var(a)=0
(ii) Var(aX)=a2Var(X)
(iii) Var(aX ± b)=Var(aX)+Var(b)= a2Var(X)
)
(X
Var
x 


30. Variances of some distributions:
Distribution Variance
Binomail dist. Var(X) = npq
Geometric dist. Var(X)= 1/ P2
Poisson dist. Var(X) = λ

31. Example
Let X be a random variable which take each of the five values
-2,0,1,3 and 4, with equal probabilities. Find the
standard deviation of Y=4X-7
Solution:
equal probabilities each value has prob.=1/5
standard deviation of Y=√var(Y)
E(X)=6/5 , E(X2)= 30/5
Var(X)=E(X2 ) – [E(X)]2
= 30/5 –(6/5)2 = 4.56
Var(Y)=Var(4X-7)=Var(4X)+Var(7)
=42 Var(X)+0 = 16 Var(X)=16 x 4.56 =72.96
standard deviation of Y=√var(Y)= √ 72.96= 8.542
x -2 0 1 3 4 sum
f(x) 1/5 1/5 1/5 1/5 1/5 1
xf(x) -2/5 0 1/5 3/5 4/5 6/5
x2f(x) 4/5 0 1/5 9/5 16/5 30/5

32. Example
If E(X) = 2, Var(X) =5 , find
1. E(2+X)2 2.Var(4+3X)
Solution:
1. E(2+X)2 =E(4+4X+X2( = 4+4E(X)+E(X2)
To get the value of E(X2) we use Var(X) =5
Var(X) = E(X2) – [E(X)]2
5 = E(X2) - 22 E(X2) = 5+4 =9
So, E(2+X)2 =E(4+4X+X2( = 4+4E(X)+E(X2)
= 4+(4x2)+9= 4+8+9=21
2.Var(4+3X)=Var(4)+32Var(X)
= 0 + (9x5) =45

33. Variance of the sum :
Def : Let X and Y be two random variables each having finite
second moments. Then X+Y has finite second moments and hence
finite variance. Now
Var(X+Y)=Var(X)+Var(Y)+2E[(X-E(X))(Y-E(Y))]
Thus unlike the mean ,the variance of a sum of two random variables is
in general not the sum of the variances. Where the quantity
E[(X-E(X))(Y-E(Y))]
Is called the covariance of X and Y and written Cov(X,Y).
Thus, we have the formula
Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)
Note that:
Cov(X,Y) = E[(X-E(X))(Y-E(Y))]
= E[XY-YE(X)-XE(Y)+E(X)E(Y)]
= E(XY) – E(X)E(Y)

34. Corollary:
If X and Y are independent then Cov(X,Y)=0
Then,
Var(X+Y) = Var(X) + Var(Y)
In general,
If X1 , X2 ,….,Xn are independent random variables each each having a finite
second moment, then
Properties of Cov(X,Y):
Let X and Y be two random variables , the Cov(X,Y) has the following
properties:
1. Symmetry , i.e.
Cov(X,Y) = Cov(Y,X)
2. Cov(a1X1 + a2X2 , b1Y1+b2Y2 ( =
= a1b1Cov(X1, Y1)+ a1b2Cov(X1, Y2) + a2b1Cov(X2, Y1)+ a2b2Cov(X2, Y2)
3. If X and Y are independent then Cov(X,Y)=0

 


n
i
i
n
i
i X
Var
X
Var
1
1
)
(
)
(

35. 4.
5. Cov(a,X) = 0 , where a is a constant.
Note that:
Var (aX+bY) =a2 Var(X)+b2 Var(Y)+2abCov(X,Y)
In general,
If X1 , X2 ,….,Xn are random variables and
Y= a1X1+ a2X2 +…….+ anXn where a1 , a2 ,….,an are constants, then
Where the double sum extends over all the values of I and j,from 1 to n
for which i< j
)
,
(
)
,
(
1 1 1
1
 
   


n
j
n
i
n
j
j
i
j
i
j
j
i
n
i
i Y
X
Cov
b
a
Y
b
X
a
Cov
)
,
(
2
)
(
)
(
1
2
j
i
j
j
i
i
i
n
i
i X
X
Cov
a
a
X
Var
a
Y
Var 
 




36. Example
If the random variable X,Y,Z have meanes,respectively,2,-3,4 and
variances 1,5,2 and Cov(X,Y)= -2,Cov(X,Z)= -1,Cov(Y,Z)=1.
Find the mean and the variance of W= 3X - Y +2Z
Solution:
E(W)=E(3X - Y +2Z)= 3E(X) – E(Y) + 2E(Z)
= (3 x2) – (-3) + 2x4
= 6 + 3 + 8 =17
Var(W) =Var(3X - Y +2Z)=Var(3X)+Var(Y)+Var(2Z)+2Cov(3X,-Y)
+ 2Cov(3X,2Z)+2Cov(-Y,2Z)
= 9Var(X)+Var(Y)+4Var(Z)+(2x3x-1)Cov(X,Y)+(2x3x2)Cov(X,Z)
+(2x-1x2)Cov(Y,Z)=(9x1)+(5)+(4x2)+(-6x-2)+(12x-1)+(-4x1)
= 9+5+8+12-12-4 = 18

37. Example
Let X and Y be two independent random variables having finite second
moments. Compute the mean and variance of 2X+3Y in terms of
those of X and Y.
Solution:
E(2X+3Y)= 2E(X)+3E(Y)
Var(2X+3Y) =
4Var(X)+9Var(Y)
Remember if X,Y indep, then
0
Y)
Cov(X, 

38. Example
If X and Y are random variables with 2 and 4 respectively and
Cov(X,Y) = -2,Find the variance of the random variable Z=3X-4Y+8
Solution:
Var(Z)=Var(3X-4Y+8)= 9Var(X)+16Var(Y)+Var(8)+2Cov(3X,-4Y)
= (9x2)+(16x4) + 0 +(2x 3x-4x-2)
= 18 + 64+ 48 =130

39. Example
If X and Y are independent random variables with variances 5 and 7
respectively ,find
1-The variance of T =X-2Y
Var(T )=Var(X-2Y)=Var(X)+4Var(Y)=5+(4x7)=33
2-The Variance of Z= -2X+3Y
Var(Z)= Var(-2X+3Y)=4 Var(x)+9Var(Y)=83
3- The Cov(T,Z)
Cov(T,Z)=Cov(X-2Y, -2X+3Y)
=Cov(X,-2X)+Cov(X,3Y)+Cov(-2Y,-2X)+Cov(-2Y,3Y)
= -2Cov(X,X)+3Cov(X,Y)+(-2x-2)Cov(Y,X)+(-2x3)Cov(Y,Y)
= -2Var(X)+(3x0) +(4x0)-6xVar(Y)
= (-2x5)+0+0 -(6x7)= -10 - 42= -52
Note:
Cov (x,x)=Var(x)
Cov(y,y)=Var(Y)

40. Correlation Coefficient:
Let X and Y be two random variables having finite variances . One
measure of the degree of dependence between the two random variables
is the correlation coefficient ρ(X,Y) defined by
These random variables are said to be uncorrelated if ρ =0
(since Cov(X,Y)=0).
If X and Y are independent ,we see at once that independent random
variables are uncorrelated (the converse is not always true) , i.e. it is
possible for dependent random variable to be uncorrelated .
)
(
)
(
)
,
(
)
,
(
Y
Var
X
Var
Y
X
Cov
Y
X 
 


41. Theorem:
 If Y= a+ bX , then











0
1
0
0
0
1
)
,
(
b
b
b
Y
X


42. Example:
Let X and Y be the random variables
with the following joint probability
Function: Find
1- E(XY) = ??
=(1x-3x0.1)+(1x2x0.2)+(1x4x0.2)+
(3x-3x0.3)+(3x2x0.1)+(3x4x0.1)=
= -0.3+0.4+0.8-2.7+0.6+1.2
= 0
XY -3 2 4 Sum
1 0.1 0.2 0.2 0.5
3 0.3 0.1 0.1 0.5
Sum 0.4 0.3 0.3 1


x y
y
x
xyf
XY
E )
,
(
)
(

43. Example (Continue)
From table:
2-E(X)=2 ,E(X2)= 5
Var(X)= E(X2)-E(X)=3
4-E(X+Y)=E(X)+E(Y)
= 2+0.6
= 2.6
From table:
3-E(Y)=0.6 ,E(Y2)= 9.6
Var(Y)= E(Y2)-E(Y)=9.24
5-Cov(X,Y)=E(XY)-E(X)E(Y)
= 0 – (2x0.6)
= - 1.2
x 1 3 sum
f(x) 0.5 0.5 1
xf(x) 0.5 1.5 2
x2f(x) 0.5 4.5 5
y -3 2 4 Sum
f(y) 0.4 0.3 0.3 1
yf(y) -1.2 0.6 1.2 0.6
y2f(y) 3.6 1.2 4.8 9.6

44. Example (Continue)
6- Var(X,Y)=Var(X)+Var(Y)+2Cov(X,Y)
= 1 + 0.6 + (2x -0.6)=0.4
7- find the correlation coefficient (ρ) ??
8- Are X and Y independent??
No , since Cov(X,Y) = -0.6 ≠0
Or
No, Since ρ has a value ,so X is related to Y
)
(
)
(
)
,
(
)
,
(
Y
Var
X
Var
Y
X
Cov
Y
X 
 
 39477
.
0
24
.
9
1
2
.
1





45. Moment Generating Function
In the following we concentrate on applications of moment generating
functions. The obvious purpose of the moment generating function is in
determining moments of distributions. However the most important
contribution is to establish distributions of functions of random variables.
Definition:
The moments generating function of the random variable X is given by
E(etx ) and denoted by Mx(t) . Hence
Mx(t)= E(etx ( = ∑etx f(x)

46. Example:
Given that the probability distribution
x= 1,2,3,4,5
Find the moment generating function of this random variable
Mx(t)= E(etx ) = ∑etx f(x)
= [ 3 et + 4 e2t +5 e3t +6e4t +7e5t ]/25
Some properties of moment generating functions:
Where a, b constant
25
2
)
(


x
x
f
)
3
(
)
(
3
)
(
)
(
2
)
3
(
)
(
1
t
M
e
t
M
t
M
e
t
M
t
M
t
M
x
bt
b
ax
x
bt
b
x
x
ax









47. Moments generating functions Mx(t) of
some distributions:
Distribution mean Var(X) Mx(t)
Binomail dist. E(X)= np Var(X) = npq
Geometric dist. E(X) = 1/p Var(X)= 1/ P2
Poisson dist. E(X) = λ Var(X) = λ
Hypergeometric
dist.
E(X) = n M / N
-- --
Uniform distribution E(X) = (N+1)/ 2
-- ---
n
t
x pe
q
t
M )
(
)
( 

t
t
x
qe
pe
t
M


1
)
(
)
1
(
)
( 

t
e
x e
t
M 

48. Example
For each of the following moment generating function, find
the mean and the variance of X
1-
The distribution is Binamail with n=4 , P=0.4
E(X)=np= 4 x 0.4 =1.6
Var(x) = npq =4x 0.4x0.6 = 0.96
2-
The distribution is Poisson with λ=6
E(X)= λ = 6
Var(X) = λ =6
4
)
6
.
0
4
.
0
(
)
( 
 t
x e
t
M
)
1
(
6
)
( 

t
e
x e
t
M

49. Example
3-
The distribution is geometric with P=0.2
E(X)= 1/P= 1/0.2 =50
Var(X) =1/P2 =1/0.22
P(X=1) = pqx-1 = pq0 = 0.2x(0.8)0=0.2
t
t
x
e
e
t
M
8
.
0
1
2
.
0
)
(



50. Example
The moment generating function of the random variable X
and Y are
If X and Y are independent ,find
1- E(XY) 2- Var(X+Y) 3 –Cov(X+2,Y-3)
Solution:
X has Poisson distribution with λ = 2 E(x)=Var(X)=λ=2
Y has Binomail distribution with n=10,P=0.75
E(Y)=10x0.75 = 7.5 ,Var(Y)= 10x0.75x0.25=0.1878
10
)
2
2
(
)
25
.
0
75
.
0
(
)
(
)
(


 
t
Y
e
X
e
t
M
e
t
M
t

51. Example
Since X and Y independent ,then
1- E(XY)=E(X)E(Y)=2x7.5=15
2- Var(X+Y)=Var(X) + Var(Y)
= 2 + 0.1878 = 2.1878
3 –Cov(X+2,Y-3)= Cov(X,Y)+Cov(X,3)+Cov(2,-3)
= 0 + 0 +0 =0

52. Thanks For Attention