Review of probability calculus

Review of probability calculus
June 11, 2017
Andreas Scheidegger
Eawag: Swiss Federal Institute of Aquatic Science and Technology

Random variables (RV)
“Mathematical machines that generate numbers”

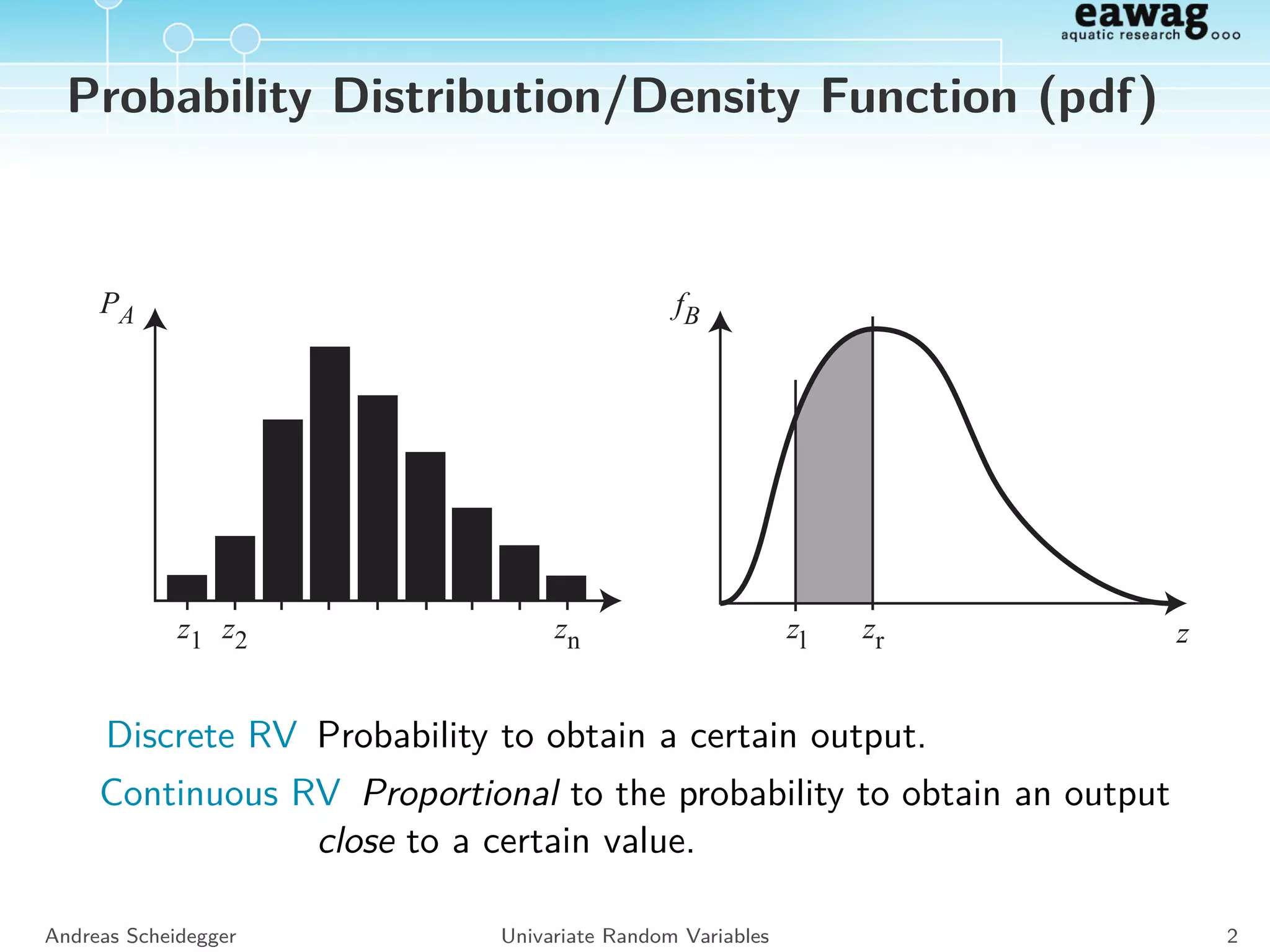
Completely described by the cumulative probability distribution
function (cdf) or the probability distribution/density function
(pdf).
Some properties can be described by measures such as mean,
variance, mode, . . .
Andreas Scheidegger Univariate Random Variables 1

Probability Distribution/Density Function (pdf)
PA fB
z1 z2 zn zzrzl
Discrete RV Probability to obtain a certain output.
Continuous RV Proportional to the probability to obtain an output
close to a certain value.

Cumulative Distribution Function (cdf)
FA FB
z1 z2 zn zzrzl
0
1
0
1
Discrete and continous RV Probability to obtain an output equal
or smaller than a certain value.

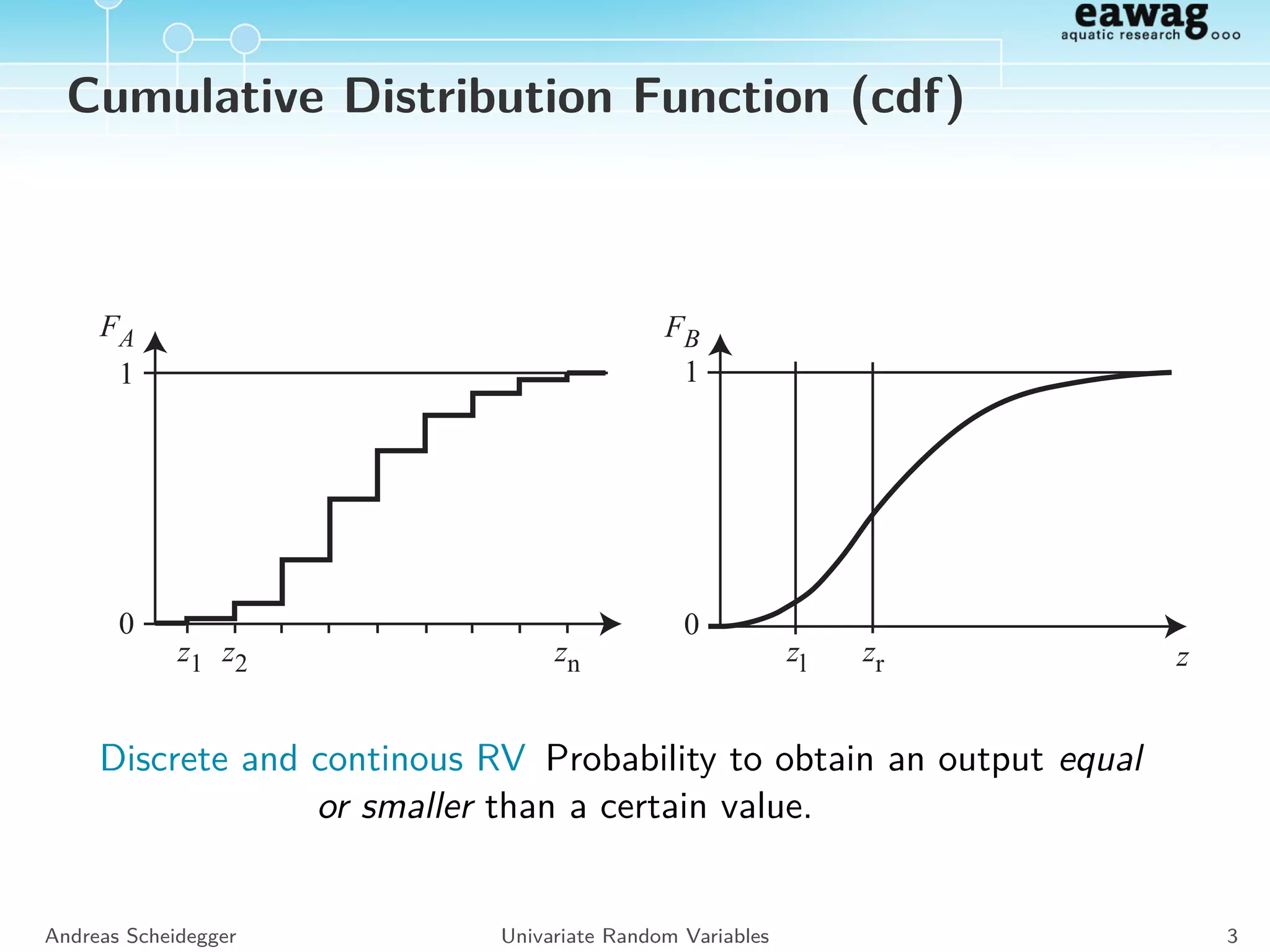
cdf and pdf
Discrete RVs
Distribution function:
FA(z) = P(A ≤ z)
Probability distribution:
PA(zi ) for zi ∈ ΩA
Continous RVs
Distribution function:
FB(z) = P(B ≤ z)
Probability density:
fB(z) =
d
dz
FB(z)
P(B ∈ [z1, z2]) =
z2
z1
fB(z) dz
P(B ∈ [z, z + ∆]) ≈ ∆ · fB(z)

Characteristics of Random Variables
Measures of Location
Expected value:
E[A] =
z∈ΩA
z PA(z) , E[B] =
ΩB
z fB(z) dz
Median:
Med[Z] : P(Z ≤ Med[Z]) = P(Z Med[Z]) = Q0.5[Z]
Quantiles:
Qp[Z] : P(Z ≤ Qp[Z]) = p and P(Z Qp[Z]) = 1 − p
Mode:
Mode[A] = arg max
zi ∈ΩA
PA(zi ) , Mode[B] = arg max
z∈ΩB
fB(z)

Expected value of a function of a RV:
E[g(A)] =
z∈ΩA
g(z)PA(z)
E[g(B)] =
ΩB
g(z)fB(z) dz

Expected value of a function of a RV:
E[g(A)] =
z∈ΩA
g(z)PA(z)
E[g(B)] =
ΩB
g(z)fB(z) dz
Attention!
E[g(X)] = g (E[X])

Measures of Extension
Variance:
Var[Z] = E Z − E[Z]
2
Standard Deviation:
SD[Z] = Var[Z]
Inter-Quantile Range:
QRp[Z] = Q(1+p)/2[Z] − Q(1−p)/2[Z]

E[aZ + b] = a E[Z] + b
E[Z1 ± Z2] = E[Z1] ± E[Z2]
Var[Z] = E[Z2
] − E[Z]2
Var[aZ + b] = a2
Var[Z]
Only if Z1 and Z2 are independent:
Var[Z1 ± Z2] = Var[Z1] + Var[Z2]

Multivariate random variables

A

Andreas Scheidegger Multivariate Random Variables 9

Joint distribution
discrete RV:
PA,B(a, b) = PA|B(a|b) · PB(b) = PB|A(b|a) · PA(a)
E.g.: PA,B(3, 1) : Probability to obtain ai = 3 and bi = 1.

Joint distribution
discrete RV:
PA,B(a, b) = PA|B(a|b) · PB(b) = PB|A(b|a) · PA(a)
E.g.: PA,B(3, 1) : Probability to obtain ai = 3 and bi = 1.
continous RV:
fA,B(a, b) = fA|B(a|b) · fB(b) = fB|A(b|a) · fA(a)
E.g.: fA,B(3, 1) : proportional to the probability to obtain a
realization close to 3 and 1.

Conditional Distributions
Discrete RV:
PA|B(a|b) =
PA,B(a, b)
PB(b)
Continuous RV:
fA|B(a|b) =
fA,B(a, b)
fB(b)

Marginal distribution
Discrete random variables:
PA(a) =
b∈ΩB
PA,B(a, b)

Marginal distribution
PA(a) =
b∈ΩB
PA,B(a, b)
Continuous random variables:
fA(a) =
ΩB
fA,B(a, b) db

Independence
Deﬁnition:
FA,B(a, b) = FA(a) · FB(b)
PA,B(a, b) = PA(a) · PB(b)
Continuous random variables:
fA,B(a, b) = fA(a) · fB(b)

Bayes’ Theorem1
Discrete random variables
Because
PA|B(a|b)PB(b) = PB|A(b|a)PA(a)
we can write
PA|B(a|b) =
PB|A(b|a)PA(a)
PB(b)
=
PB|A(b|a)PA(a)
a ∈ΩA
PB|A(b|a )PA(a )
1
Bayes’ Theorem as we know it today was actually formulated by P. Laplace
in 1774 and not by T. Bayes.

Bayes’ Theorem
Continuous random variables
fA|B(a|b) =
fB|A(b|a)fA(a)
fB(b)
=
fB|A(b|a)fA(a)
fB|A(b|a )fA(a ) da

Dependencies
Variance-Covariance Matrix:
Var[Z] = E Z − E[Z] Z − E[Z]
T
Individual Covariances:
Cov[Zi , Zj] = E Zi − E[Zi ] Zj − E[Zj] = Var[Z]i,j
Correlation Matrix:
Cor[Z]i,j =
Cov[Zi , Zj]
Var[Zi ] · Var[Zj]

Correlation
Correlation measures only linear dependencies!
Figure: Several sets of (x, y) points, with the correlation coeﬃcient of x
and y for each set. Source: Wikipedia.

Short Notation
Function argument corresponds to RV
PA(a), PB|A(b|a) ←→ P(a), P(b|a)
fB(b), fA|B(a|b) ←→ f (b), f (a|b) or p(b), p(a|b)
Example:
fX1|X2,X3
(x1|x2, x3) =
fX2|X1
(x2|x1)fX1|X3
(x1|x3)
fX2 (x2)
p(x1|x2, x3) =
p(x2|x1)p(x1|x3)
p(x2)

Directed Acyclic Graphs
Visualize independence structure of RV
A
B
DC

Directed Acyclic Graphs
Visualize independence structure of RV
A
B
DC
p(A)
p(B | A)
p(C | A, B)
p(D | B)
e.g. A and D are conditionally
independent. joint distribution:
p(A, B, C, D) =
p(A) p(B | A) p(C | A, B) p(D | B)

Normal distribution
Andreas Scheidegger Normal distributions 20

Central Limit Theorem
Lets X1, X2, . . . be independent and identically distributed RVs
with mean µ and a ﬁnite variance σ2. Further we deﬁne
Sn = X1 + X2 + . . . + Xn, that has a mean nµ and variance nσ2.
Then the standardized RV
Zn =
Sn − nµ
√
nσ
is standard normal distributed for n → ∞.

Central Limit Theorem Example
n = 1
Density
−2 −1 0 1 2
0.00.40.8
n = 2
Density
−2 −1 0 1 2
0.00.30.6
n = 3
Density
−2 −1 0 1 2
0.00.30.6
n = 4
Density
−2 −1 0 1 2
0.00.20.4
n = 5
Density
−2 −1 0 1 2
0.00.20.4
n = 6
Density
−2 −1 0 1 2
0.00.20.4
n = 7
Density
−2 −1 0 1 2
0.00.20.4
n = 8
Density
−2 −1 0 1 2
0.00.20.4
n = 9
Density
−2 −1 0 1 2
0.00.20.4
n = 10
Density
−2 −1 0 1 2
0.00.20.4
n = 11
Density
−2 −1 0 1 2
0.00.20.4
n = 12
Density
−2 −1 0 1 2
0.00.20.4

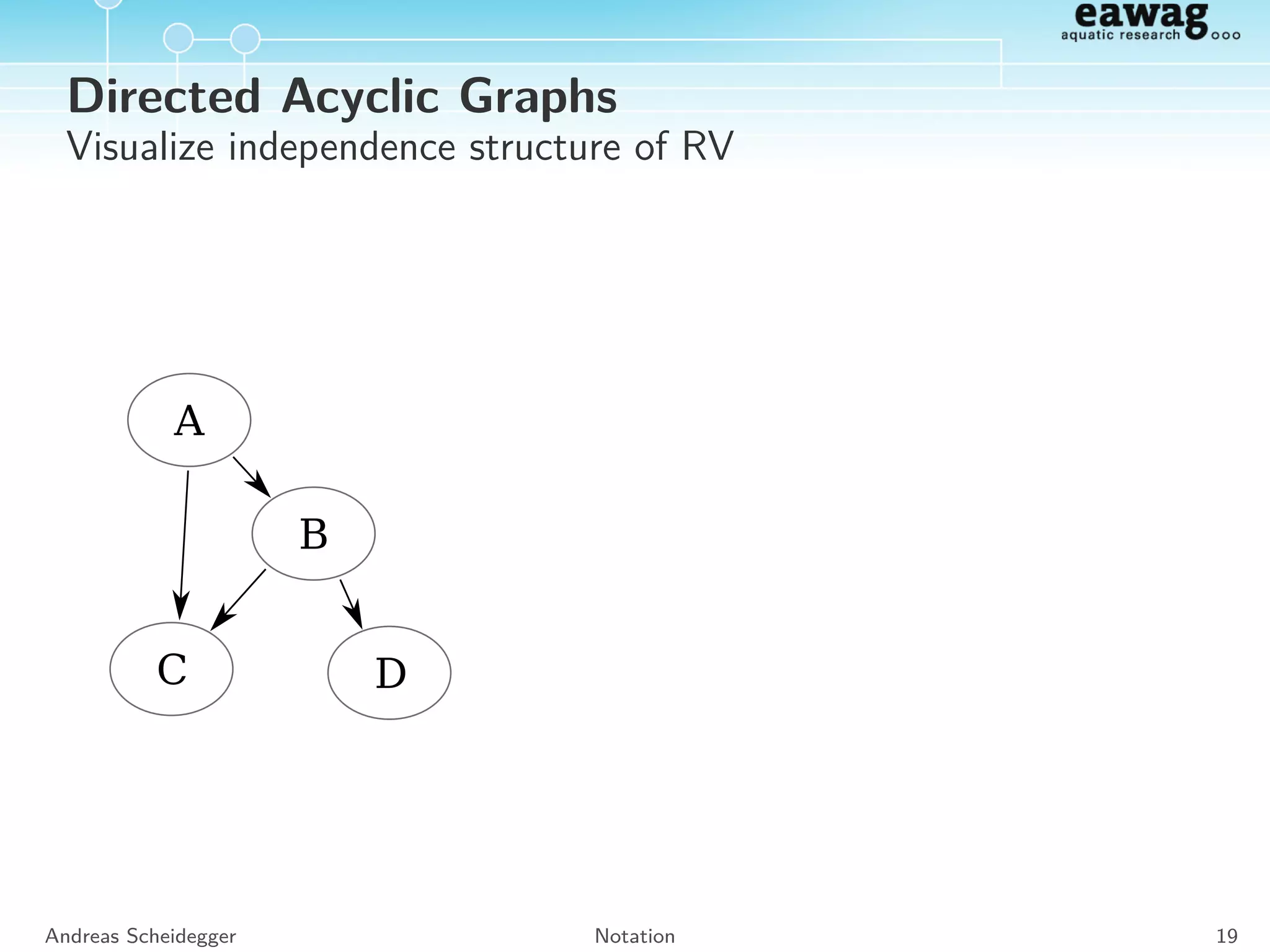
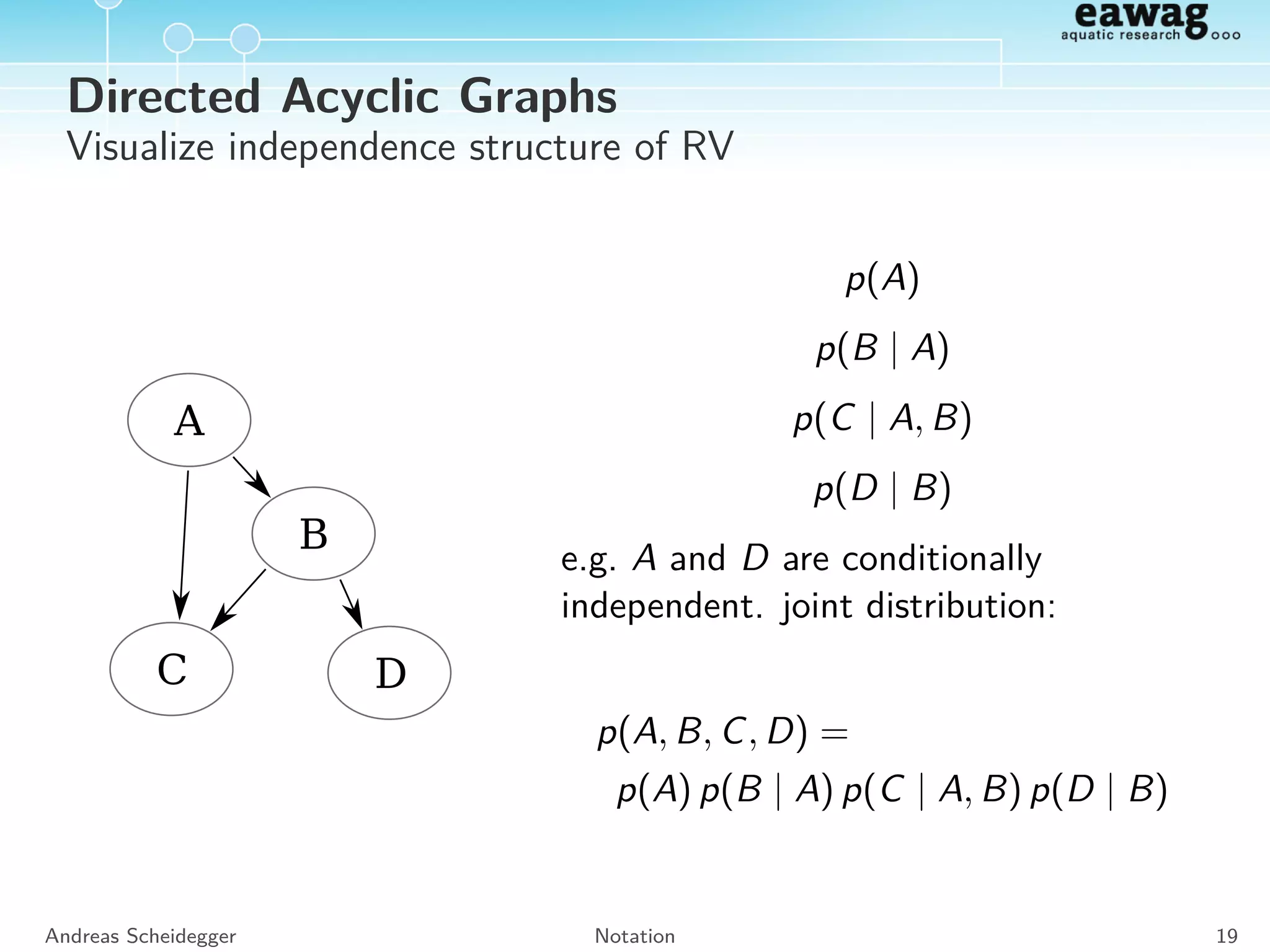
Relationships of Univariate Distributions
Figure 1. Univariate distribution relationships.
The American Statistician, February 2008, Vol. 62, No. 1 47
Downloadedby[Lib4RI]at02:2428May2013
at02:2428May2013
From: Leemis, L. M. and McQueston, J. T. (2008) Univariate distribution
relationships. The American Statistician, 62(1), 45–53. → Link

Multivariate Normal Distribution
Density of a multivariate Normal distribution of dimension n with a
mean vector µ and a variance-covariance matrix Σ:
Z ∼ N(µ, Σ)
fN(µ,σ,R)(z) =
1
(2π)n/2
1
| Σ |1/2
exp −
1
2
(z − µ)T
Σ−1
(z − µ)

Properties
All marginals are normal distributed
Z ∼ N(µ, Σ) ⇒ Zi ∼ N(µi , Σi,i )

Properties
Z ∼ N(µ, Σ) ⇒ Zi ∼ N(µi , Σi,i )
Linear transformation:
Z ∼ N(µ, Σ) ⇒ AZ + b ∼ N Aµ + b, AΣAT

Properties
Z ∼ N(µ, Σ) ⇒ Zi ∼ N(µi , Σi,i )
Linear transformation:
Z ∼ N(µ, Σ) ⇒ AZ + b ∼ N Aµ + b, AΣAT
Conditional distribution:
Z =
X
Y
∼ N
µX
µY
,
ΣX,X ΣX,Y
ΣT
X,Y ΣY,Y
⇒ X | Y (y) ∼ N µX + ΣX,YΣ−1
Y,Y(y − µY), ΣX,X − ΣX,YΣ−1
Y,YΣT
X,Y

Further Generalization
one-dimensional

what’s next?
Andreas Scheidegger Random Processes 26

Discrete random process
“Random vectors with inﬁnity large number of elements”
(0.11, 10.78, -10.24, -3.90, 5.91, ...)
(-1.11, -4.06, -8.64, -0.92, -2.27, ...)
(0.76, -8.54, 0.81, 2.03, 12.9, ...)

Continous random processes
“Random functions”

What is a Probability?
Interpretation of probabilities
1. The probability for “head” is 1/2.
2. The probability that it rains tomorrow is 30%.
Frequentist Subjective
Other probability interpretations:
→ http://www.webcitation.org/6YupVo9zG
Andreas Scheidegger Interpretation 29

Frequentist
1. The frequency that “head”
occurs if the random
experiment is repeated.
Subjective
1. Somebody’s belief that a
coin toss results in “head”,
given his/her experience.

Frequentist
1. The frequency that “head”
occurs if the random
experiment is repeated.
2. “Rain tomorrow” is not a
repeatable experiment
Subjective
1. Somebody’s belief that a
coin toss results in “head”,
given his/her experience.
2. Somebody’s belief that it
rains tomorrow, given
his/her experience.

Summary
joint = conditional x marginal
f (a, b) = f (a|b) f (b) = f (b|a) f (a)
Marginals:
f (a) = f (a, b) db = f (a|b) f (b) db
More information in Appendix A.2 – A.5.
Andreas Scheidegger Summary 30

Common distributions

Implemented distribution in R
For all distributions four functions are implemented:
d__(x, ...) pdf evaluated at x
p__(x, ...) cdf evaluated at x
q__(p, ...) p-th quantile
r__(n, ...) sample n random numbers
beta *beta binomial *binom
Cauchy *cauchy chi-squared *chisq
exponential *exp F *f
gamma *gamma geometric *geom
hypergeometric *hyper log-normal *lnorm
multinomial *multinom negative binomial *nbinom
normal *norm Poisson *pois
Student’s t *t uniform *unif
Weibull *weibull

Normal Distribution
Density
Z ∼ N(µ, σ) fN(µ,σ)(z) =
1
σ
√
2π
exp −
(z − µ)2
2σ2
−3 −2 −1 0 1 2 3
012345
Normal with mean=0
z
f
sd = 0.1
sd = 0.25
sd = 0.5
sd = 1
sd = 2
sd = 4
−3 −2 −1 0 1 2 3
0.00.20.40.60.81.0
Normal with mean=0
z
F
sd = 0.1
sd = 0.25
sd = 0.5
sd = 1
sd = 2
sd = 4

Normal Distribution
Properties
E N(µ, σ) = Mode N(µ, σ) = Med N(µ, σ) = µ
SD N(µ, σ) = σ
Central limit theorem:
Lets X1, X2, . . . be independent and identically distributed RVs
with mean µ and a ﬁnite variance σ2. Further we deﬁne
Sn = X1 + X2 + . . . + Xn, that has a mean nµ and variance nσ2.
Then the standardized RV
Zn =
Sn − nµ
√
nσ
is standard normal distributed for n → ∞.

Lognormal Distribution
Deﬁnition:
Z = exp(X) , X ∼ N(m, s)
Density:
Z ∼ LN(µ, σ)
fLN(µ,σ)(z) =



1
√
2π
1
sz
exp





−
1
2
log
z
µ
+
s2
2
2
s2





for z 0
0 for z ≤ 0
with
s = log 1 +
σ2
µ2

0.0 0.5 1.0 1.5 2.0 2.5 3.0
012345
Lognormal with mean=1
z
f
sd = 0.1
sd = 0.25
sd = 0.5
sd = 1
sd = 2
sd = 4
0.0 0.5 1.0 1.5 2.0 2.5 3.0
0.00.20.40.60.81.0
Lognormal with mean=1
z
F
sd = 0.1
sd = 0.25
sd = 0.5
sd = 1
sd = 2
sd = 4

Properties
E LN(µ, σ) = µ
Mode LN(µ, σ) =
µ
1 +
σ2
µ2
3
2
Med LN(µ, σ) =
µ
1 +
σ2
µ2
SD LN(µ, σ) = σ

R implementation
Attention: The lognormal distribution in R is deﬁned with m and s
(the mean and standard deviation of X)!
The code below computes the arguments if mean µ and standard
deviation σ are given:
## conversion , ’mu ’ and ’sigma ’ given
meanlog - log(mu) - 0.5*log(1 + (sigma/mu )^2)
sdlog - sqrt(log(1 + sigma ^2/(mu ^2)))
## generate 1000 random samples
rlnorm (1000 , meanlog=meanlog , sdlog=sdlog)

χ2
Distribution
Deﬁnition:
Z =
n
i=1
X2
i , Xi ∼ N(0, 1)
Density:
Z ∼ χ2
n fχ2
n
(z) =
z(n−2)/2 exp(−z/2)
2n/2 Γ(n/2)

χ2
Distribution
0 2 4 6 8 10 12 14
0.00.10.20.30.40.50.6
χ2
z
f
df = 1
df = 2
df = 3
df = 4
df = 5
df = 10
0 2 4 6 8 10 12 14
0.00.20.40.60.81.0
χ2
z
F
df = 1
df = 2
df = 3
df = 4
df = 5
df = 10

χ2
Distribution
Properties
E χ2
n = n
Mode χ2
n = n − 2 for n ≥ 2
SD χ2
n =
√
2n

F Distribution
Deﬁnition:
Z =
X
n
Y
m
, X ∼ χ2
n , Y ∼ χ2
m
Density:
Z ∼ Fn,m fFn,m (z) =
Γ (n + m)/2 (n/m)n/2 z(n−2)/2
Γ n/2 Γ m/2

F Distribution
0 1 2 3 4
0.00.20.40.60.81.01.2
F
z
f
df1 = 2 df2 = 10
df1 = 3 df2 = 10
df1 = 5 df2 = 10
df1 = 5 df2 = 100
0 1 2 3 4
0.00.20.40.60.81.0
F
z
F
df1 = 2 df2 = 10
df1 = 3 df2 = 10
df1 = 5 df2 = 10
df1 = 5 df2 = 100

F Distribution
Properties
E Fn,m =
m
m − 2
for m 2
Mode Fn,m =
m(n − 2)
n(m + 2)
for n 2
SD Fn,m =
2m2(n + m − 2)
n(m − 2)2(m − 4)
for m 4

t Distribution
Deﬁnition:
Z =
X
Y
n
, X ∼ N(0, 1) , Y ∼ χ2
n
Density:
Z ∼ tn ftn (z) =
Γ (n + 1)/2
√
π n Γ n/2 (1 + z2/n)(n+1)/2

Review of probability calculus

More Related Content

What's hot

Similar to Review of probability calculus

More from Andreas Scheidegger

Recently uploaded

Review of probability calculus