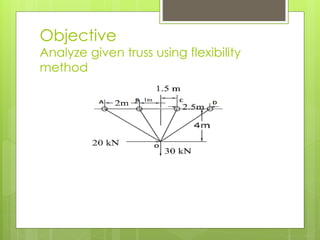
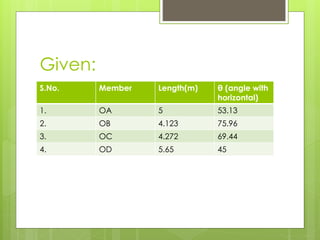
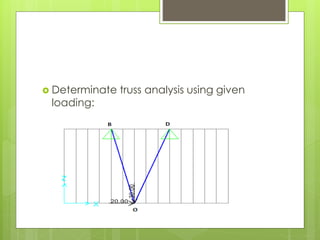
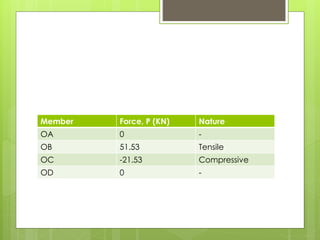
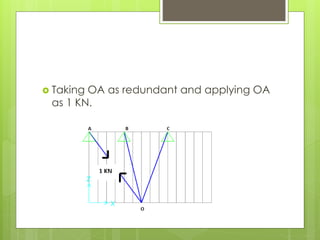
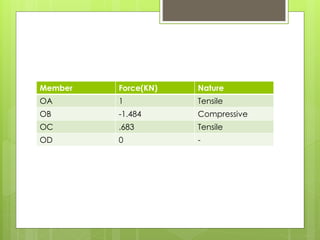
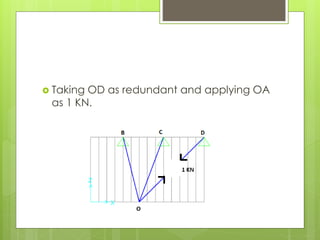
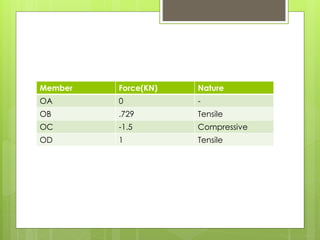
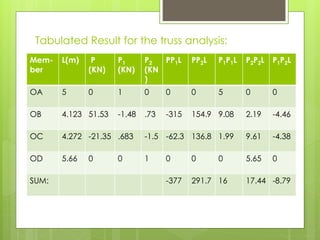
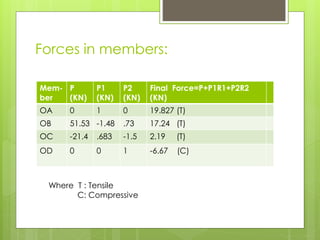
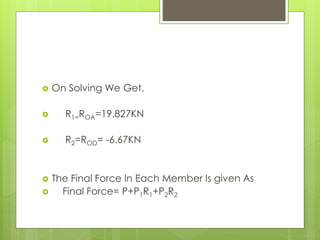This document analyzes an indeterminate truss using the flexibility method. It first calculates the static degree of indeterminacy as 2. It then selects members OA and OD as redundant members. The truss is analyzed when each redundant member is given a force of 1 kN. A flexibility matrix equation is developed and solved to determine the redundant forces, which are then used to calculate the final forces in each member. The final forces show member OA in tension and member OD in compression.

1. ASA Assignment
Analysis of indeterminate truss
using flexibility method
Prepared by:
Upendra Pandey
BT11CIV042

2. Objective
Analyze given truss using flexibility
method

3. Given:
S.No. Member Length(m) θ (angle with
horizontal)
1. OA 5 53.13
2. OB 4.123 75.96
3. OC 4.272 69.44
4. OD 5.65 45

4. Steps For Analysis
 Calculation Of Static Degree Of Indeterminacy
Of The Structure.
 For The Given Problem, Static Degree Of
Indeterminacy is 02.
 External Indeterminacy=5
 Internal Indeterminacy=-3
 Selection Of Redundant Forces To Make The
Structure Determinate.
For Simplicity, Redundant Forces members
Selected are:- OA and OD

5. 1 Therefore,
 
  
  

  


 
R
OA
R
OD
R
R
R
2
Standard Assumption :-
Tensile Force = Positive
Compressive Force= Negative

6.  Determinate truss analysis using given
loading:

7. Member Force, P (KN) Nature
OA 0 -
OB 51.53 Tensile
OC -21.53 Compressive
OD 0 -

8.  Taking OA as redundant and applying OA
as 1 KN.

9. Member Force(KN) Nature
OA 1 Tensile
OB -1.484 Compressive
OC .683 Tensile
OD 0 -

10.  Taking OD as redundant and applying OA
as 1 KN.

11. Member Force(KN) Nature
OA 0 -
OB .729 Tensile
OC -1.5 Compressive
OD 1 Tensile

12. Tabulated Result for the truss analysis:
Mem-ber
L(m) P
(KN)
P1
(KN)
P2
(KN
)
PP1L PP2L P1P1L P2P2L P1P2L
OA 5 0 1 0 0 0 5 0 0
OB 4.123 51.53 -1.48 .73 -315 154.9 9.08 2.19 -4.46
OC 4.272 -21.35 .683 -1.5 -62.3 136.8 1.99 9.61 -4.38
OD 5.66 0 0 1 0 0 0 5.65 0
SUM: -377 291.7 16 17.44 -8.79

13. ........(1)
PP L
1 375.88
1 01
AE AE
R ROA

    
.............(2)
PP L
2 290.63
R 2  ROD   02
 
AE AE

14. 
 
P P L
AE AE
f f
P L
AE AE
f
8.787
16
1 2
12 21
2
1
11


  
P L
AE AE
f
17.442 2
2
22  

15. Compatibility equation:
f R f R
    
1
2
11 1 12 2 01
f R f R
    
21 1 22 2 02
Here, 1  2  0
The Final Equation in Flexibility Matrix
Form is :-
  
1 377.58
  

1

R AE
  
  


1 16 8.787
 


291.7
8.787 17.442
2
R
AE

16.  On Solving We Get,
 R1=ROA=19.827KN
 R2=ROD= -6.67KN
 The Final Force In Each Member Is given As
 Final Force= P+P1R1+P2R2

17. Forces in members:
Mem-ber
P
(KN)
P1
(KN)
P2
(KN)
Final Force=P+P1R1+P2R2
(KN)
OA 0 1 0 19.827 (T)
OB 51.53 -1.48 .73 17.24 (T)
OC -21.4 .683 -1.5 2.19 (T)
OD 0 0 1 -6.67 (C)
Where T : Tensile
C: Compressive

18.  Thank you!!!!