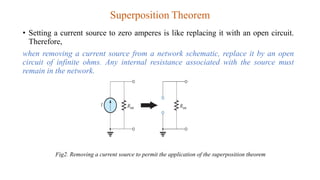
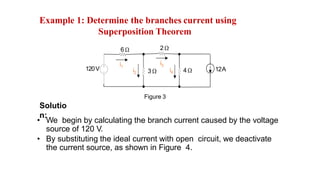
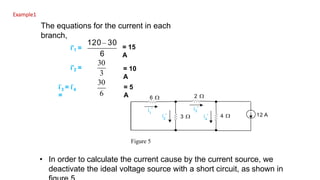
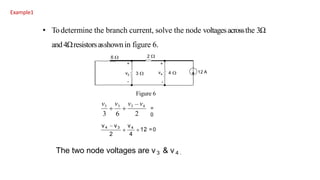
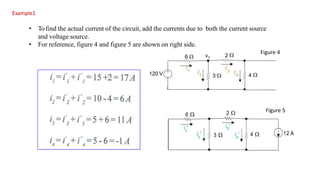
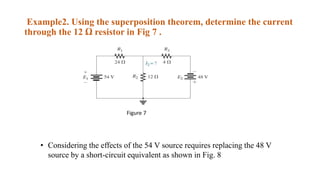
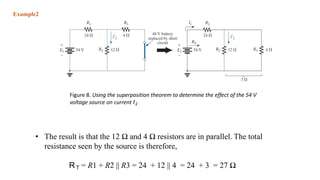
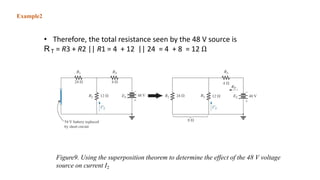
The superposition theorem allows engineers to solve for unknown voltages and currents in circuits with multiple sources. It states that the total response of a linear system to excitations is the sum of the responses that would occur due to each excitation individually. To use the theorem, each source is solved for separately while replacing other sources with their open or short circuit equivalents. The individual solutions are then combined through algebraic addition or subtraction to obtain the total solution. The document provides examples demonstrating how to use the superposition theorem to solve for branch currents in circuits with both voltage and current sources.

1. Superposition Theorem
By
Rajni Maurya
MITS, Gwalior
rajni.maurya2790@gmail.com

2. Superposition Theorem
• It is used to find the solution to networks with two or more sources that are
not in series or parallel
• The current through, or voltage across, an element in a linear bilateral network is
equal to the algebraic sum of the currents or voltages produced independently
by each source.
• This theorem allows us to find a solution for a current or voltage using only one
source at a time. Once we have the solution for each source, we can combine
the results to obtain the total solution.
• If we are to consider the effects of each source, the other sources obviously
must be removed.

3. Superposition Theorem
• Setting a voltage source to zero volts is like placing a short circuit across its
terminals. Therefore,
when removing a voltage source from a network schematic, replace it with a direct
connection (short circuit) of zero ohms. Any internal resistance associated with the
source must remain in the network.
Fig1. Removing a voltage source to permit the application of the superposition theorem

4. Superposition Theorem
• Setting a current source to zero amperes is like replacing it with an open circuit.
Therefore,
when removing a current source from a network schematic, replace it by an open
circuit of infinite ohms. Any internal resistance associated with the source must
remain in the network.
Fig2. Removing a current source to permit the application of the superposition theorem

5. Superposition Theorem
Since the effect of each source will be determined independently, the number of
networks to be analyzed will equal the number of sources.
• For a two-source network, if the current produced by one source is in one
direction, while that produced by the other is in the opposite direction through the
same resistor, the resulting current is the difference of the two and has the
direction of the larger.
If the individual currents are in the same direction, the resulting current is the
sum of two in the direction of either current.

6. Superposition Theorem
• Similarly, if a particular voltage of a network is to be determined, the contribution to
that voltage must be determined for each source.
When the effect of each source has been determined, those voltages with the
same polarity are added, and those with the opposite polarity are subtracted; the
algebraic sum is being determined.
The total result has the polarity of the larger sum and the magnitude of the difference.

7. Example 1: Determine the branches current using
Superposition Theorem
Solutio
n:
• We begin by calculating the branch current caused by the voltage
source of 120 V.
• By substituting the ideal current with open circuit, we deactivate
the current source, as shown in Figure 4.
120V 3
6
12A4
2
i1
i2
i3
i4
Figure 3

8. 120 V 3
6
4
2
i'
1
i'
2
i'
3
i'
4
v1
Figure 4
• To calculate the branch current, the node voltage across
the 3Ω resistor must be known. Therefore
v1 120 v1 v1
= 0
6 3 2 4
where v1 = 30 V
Example1

9. 120 30
6
30
= 15
A
i'2 =
3
30
= 10
A
i'
3 = i'
4
= 6
= 5
A
• In order to calculate the current cause by the current source, we
deactivate the ideal voltage source with a short circuit, as shown in
3
6
12 A4
2
1
i "
2
i "
i3
"
4
i "
i'1 =
Figure 5
Example1
The equations for the current in each
branch,

10. • Todetermine the branch current, solve the node voltagesacrossthe 3Ω
and4Ωresistorsasshownin figure 6.
The two node voltages are v 3 & v 4 .
12 A
6 2
+ +
v3 3 v4 4
- -
2
2 4
v3 v3 v3 v4
3 6
v4 v3 v4
12 =0
=
0
Figure 6
Example1

11. • By solving these equations, we obtain
v3 = -12 V
v4 = -24V
Now we can find the branches current as shown
in figure 5 .
Example1

12. • Tofind the actual current of the circuit, add the currents due to both the current source
and voltage source.
• For reference, figure 4 and figure 5 are shown on right side.
Figure 4
Figure 5
Example1

13. Example2. Using the superposition theorem, determine the current
through the 12 Ω resistor in Fig 7 .
• Considering the effects of the 54 V source requires replacing the 48 V
source by a short-circuit equivalent as shown in Fig. 8
Figure 7

14. Figure 8. Using the superposition theorem to determine the effect of the 54 V
voltage source on current I2
• The result is that the 12 Ω and 4 Ω resistors are in parallel. The total
resistance seen by the source is therefore,
RT = R1 + R2 || R3 = 24 + 12 || 4 = 24 + 3 = 27 Ω
Example2

15. • and the source current is
𝐼𝑆 =
𝐸1
𝑅 𝑇
=
54 𝑉
27 Ω
= 2 𝐴
• Using the current divider rule results in the contribution to I2 due to
the 54 V source:
𝐼2
′
=
𝑅3 𝐼 𝑆
𝑅3+ 𝑅2
=
4 Ω 2𝐴
4 Ω + 12 Ω
= 0.5 𝐴
• Now replace the 54 V source by a short-circuit equivalent, the
network in Fig. 9 results. The result is a parallel connection for the
12 Ω and 24 Ω resistors.
Example2

16. • Therefore, the total resistance seen by the 48 V source is
RT = R3 + R2 || R1 = 4 + 12 || 24 = 4 + 8 = 12 Ω
Figure9. Using the superposition theorem to determine the effect of the 48 V voltage
source on current I2
Example2

17. • And the source current is
𝐼𝑆 =
𝐸2
𝑅 𝑇
=
48 𝑉
12 Ω
= 4 𝐴
• Apply the current divider rule results in
𝐼2
′′
=
𝑅1 𝐼 𝑆
𝑅1+ 𝑅2
=
24 Ω 4𝐴
24 Ω + 12 Ω
= 2.67 𝐴
• Current 𝐼2 due to each source has a different
direction, as shown in Fig 11. The net
current therefore is the difference of the two
and in the direction of the larger as follows:
𝐼2 = 𝐼2
′′
- 𝐼2
′
= 2.67 A - 0.5 A = 2.17 A
Figure 10. Using the
results of Fig8 and Fig9
to determine current 𝐼2
Example2

18. Thanks