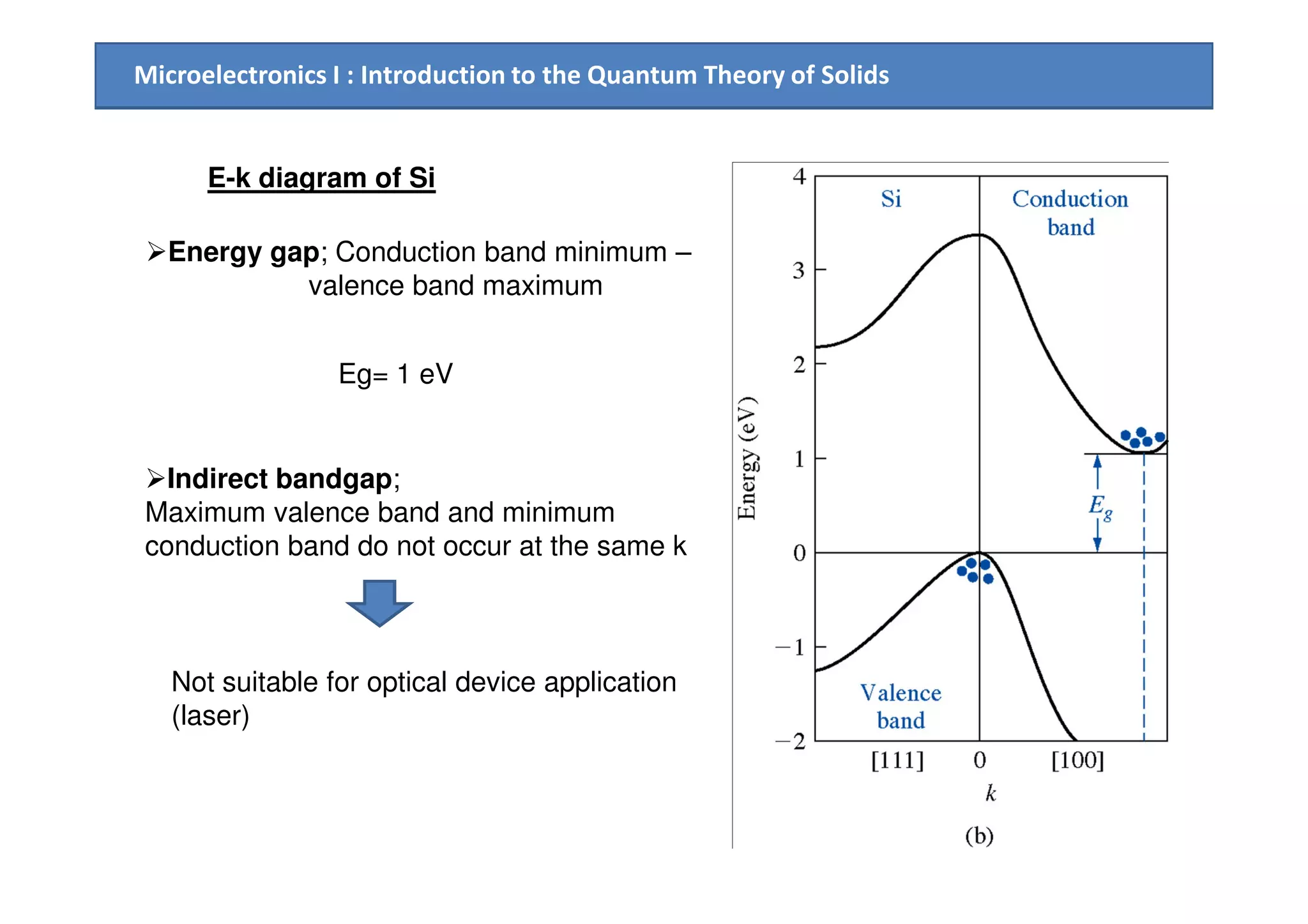
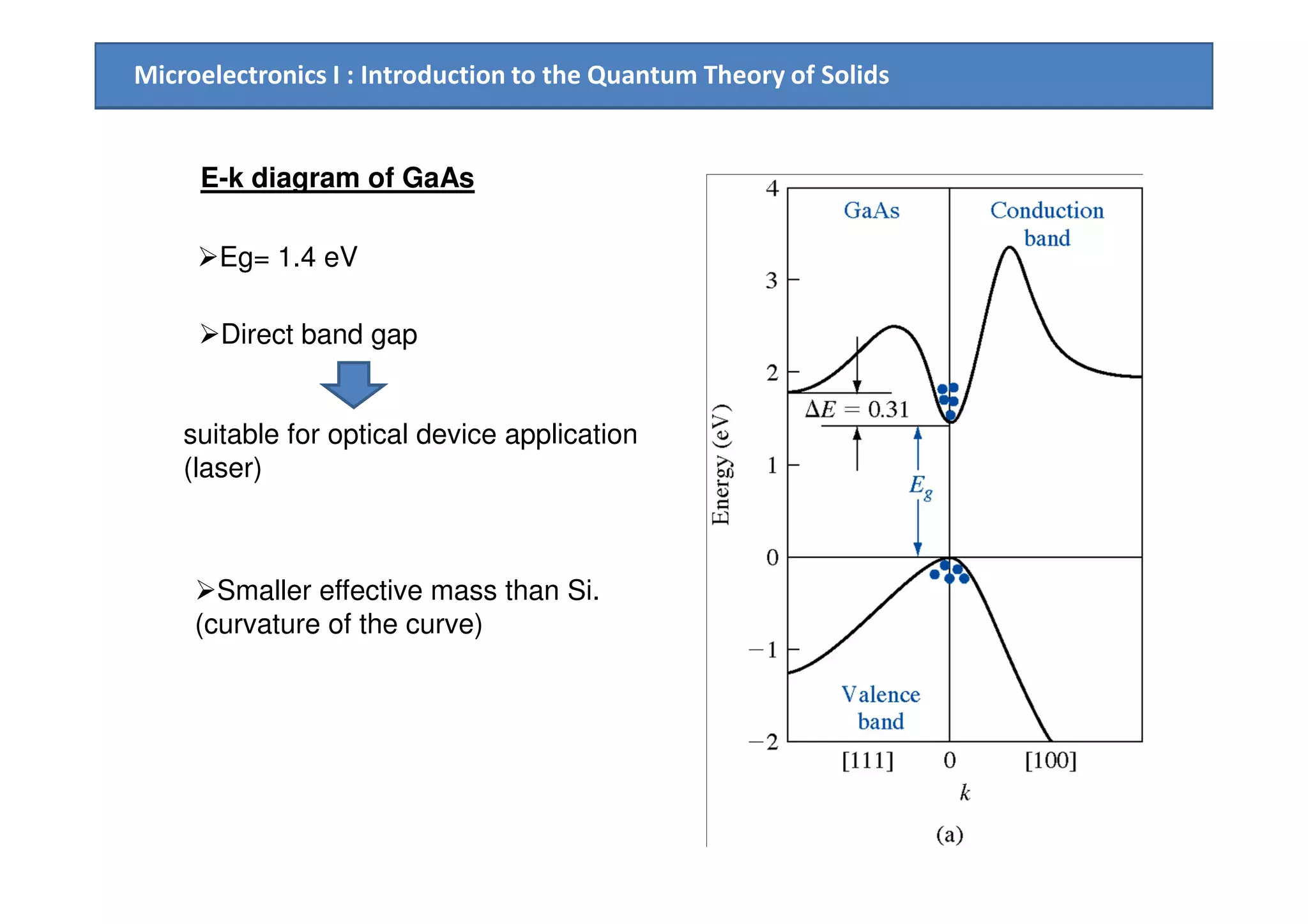
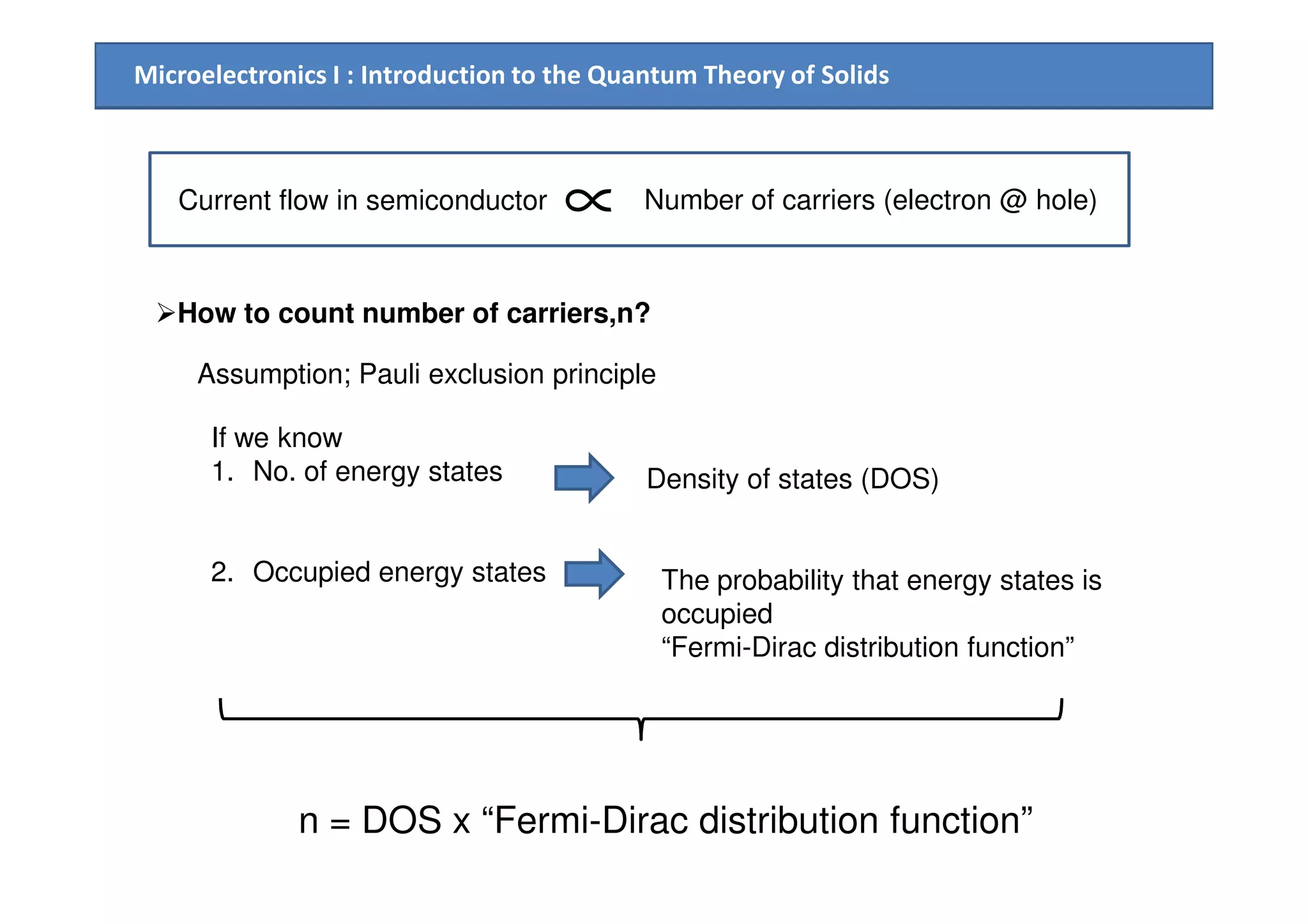
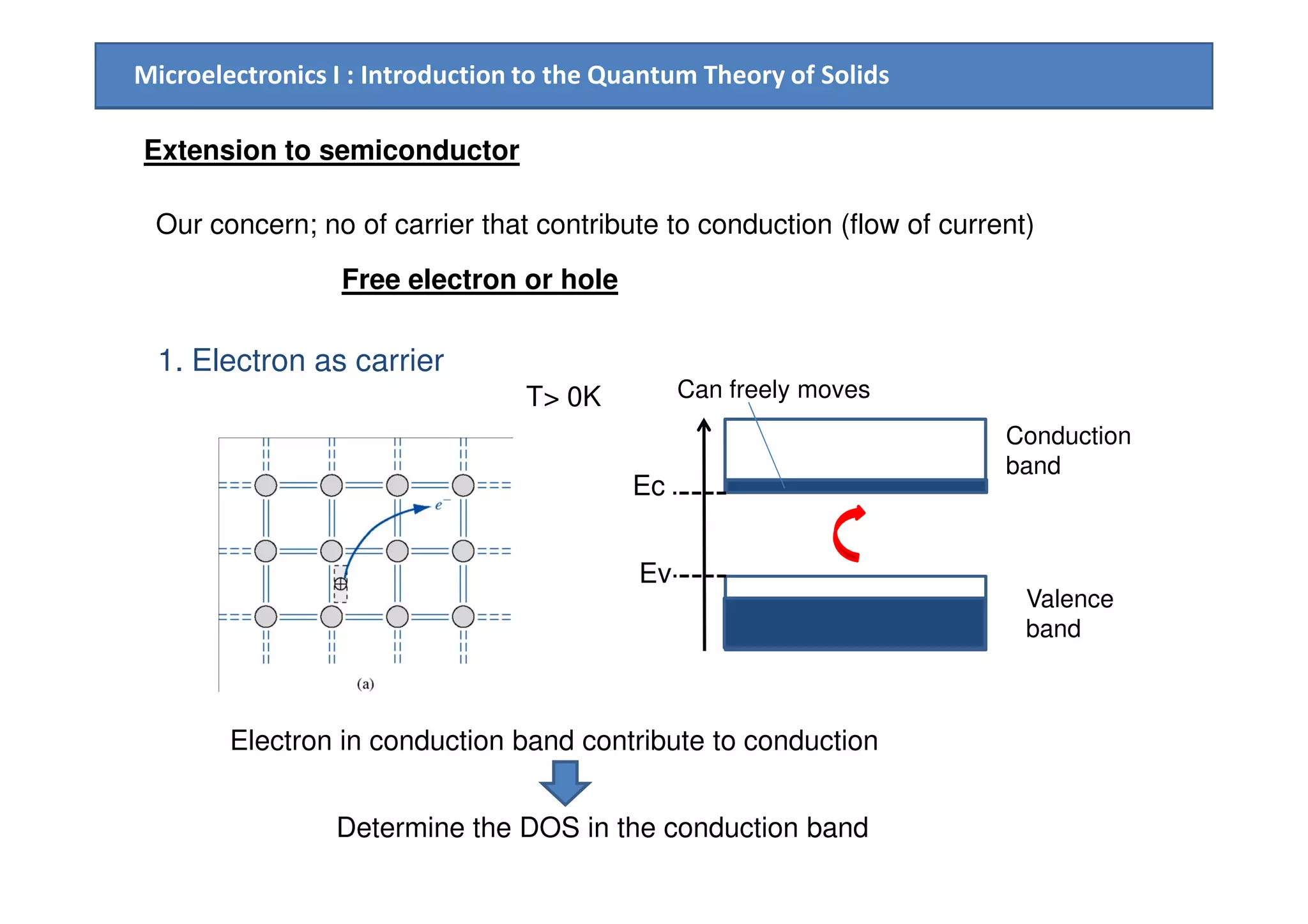
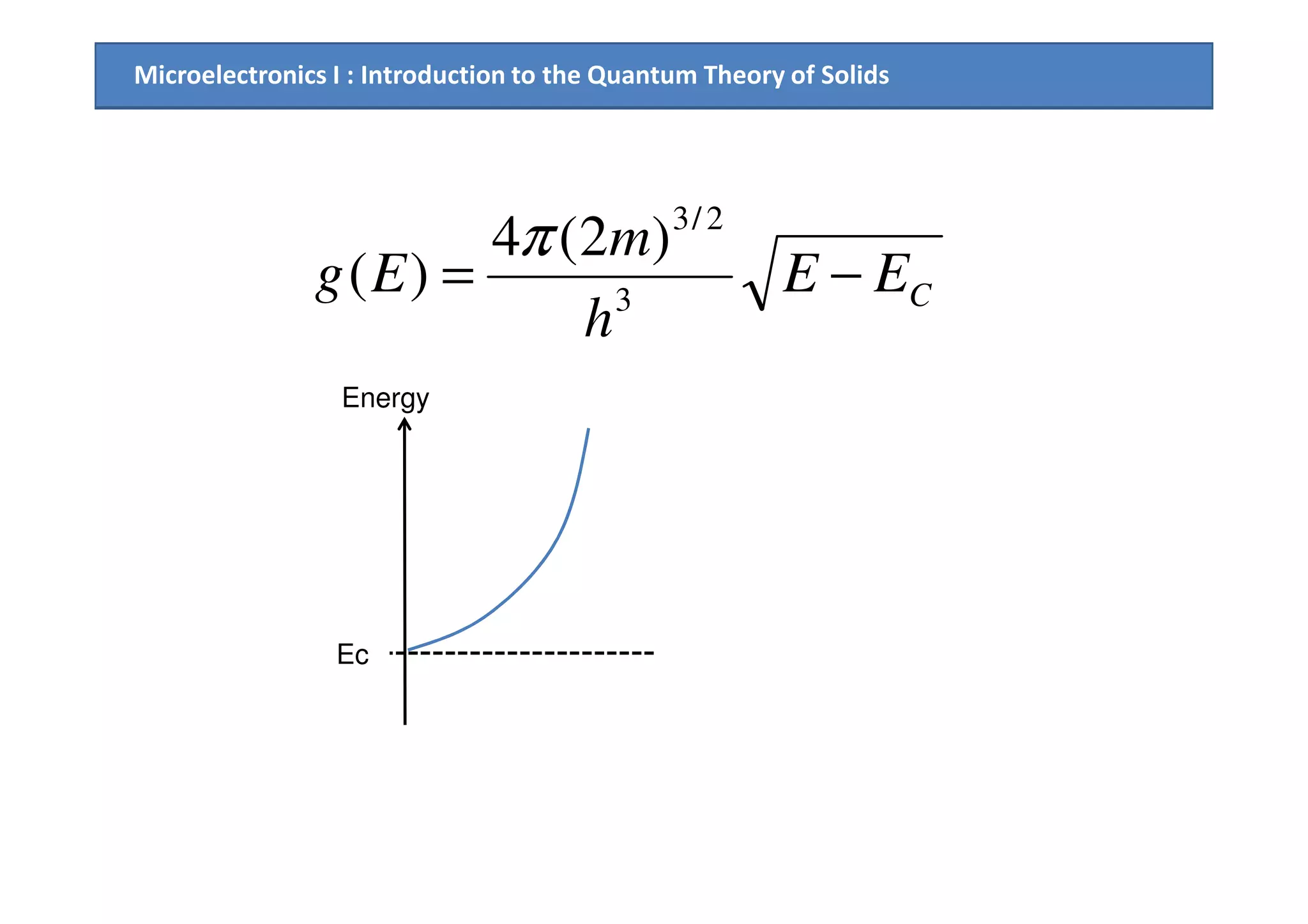
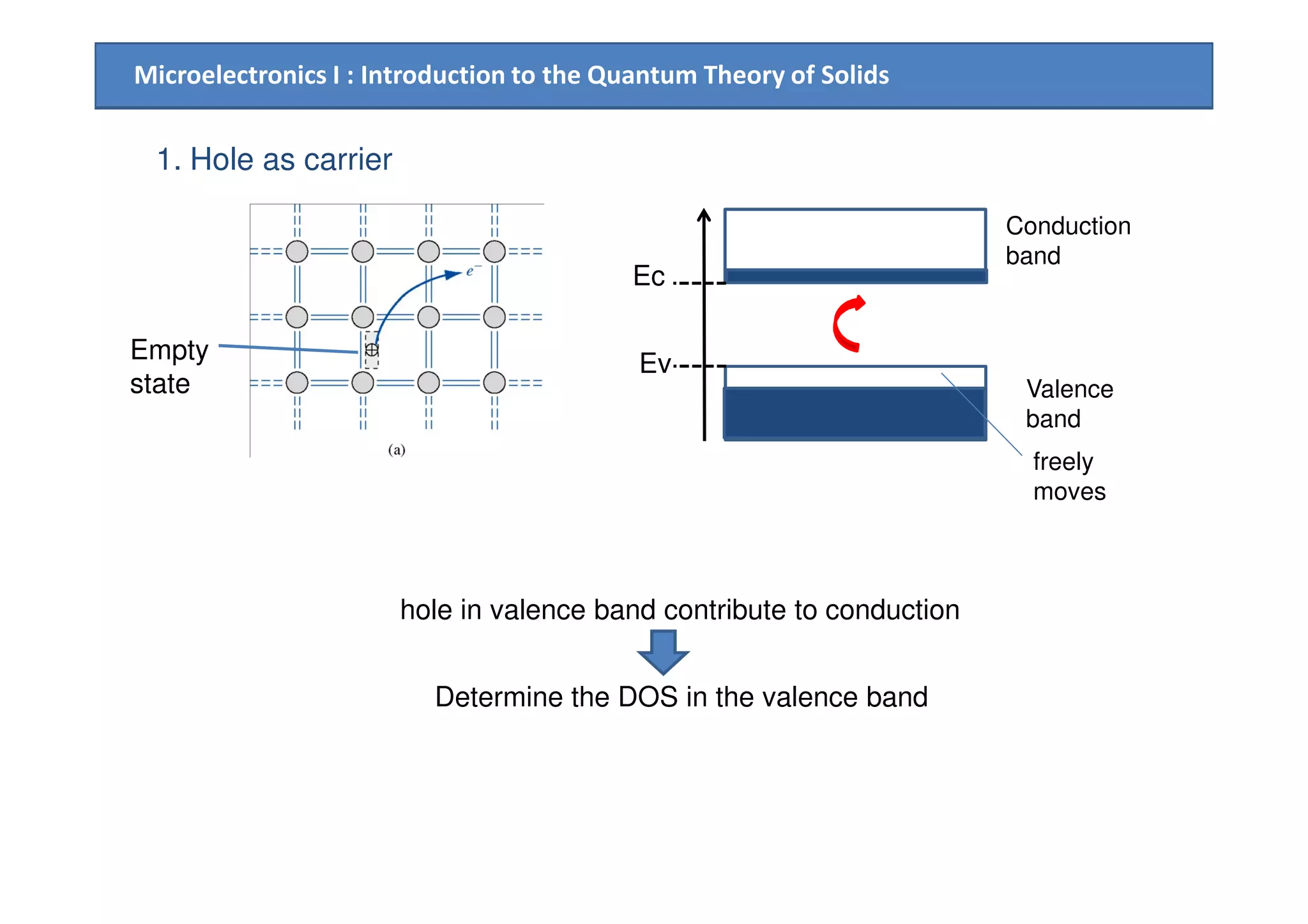
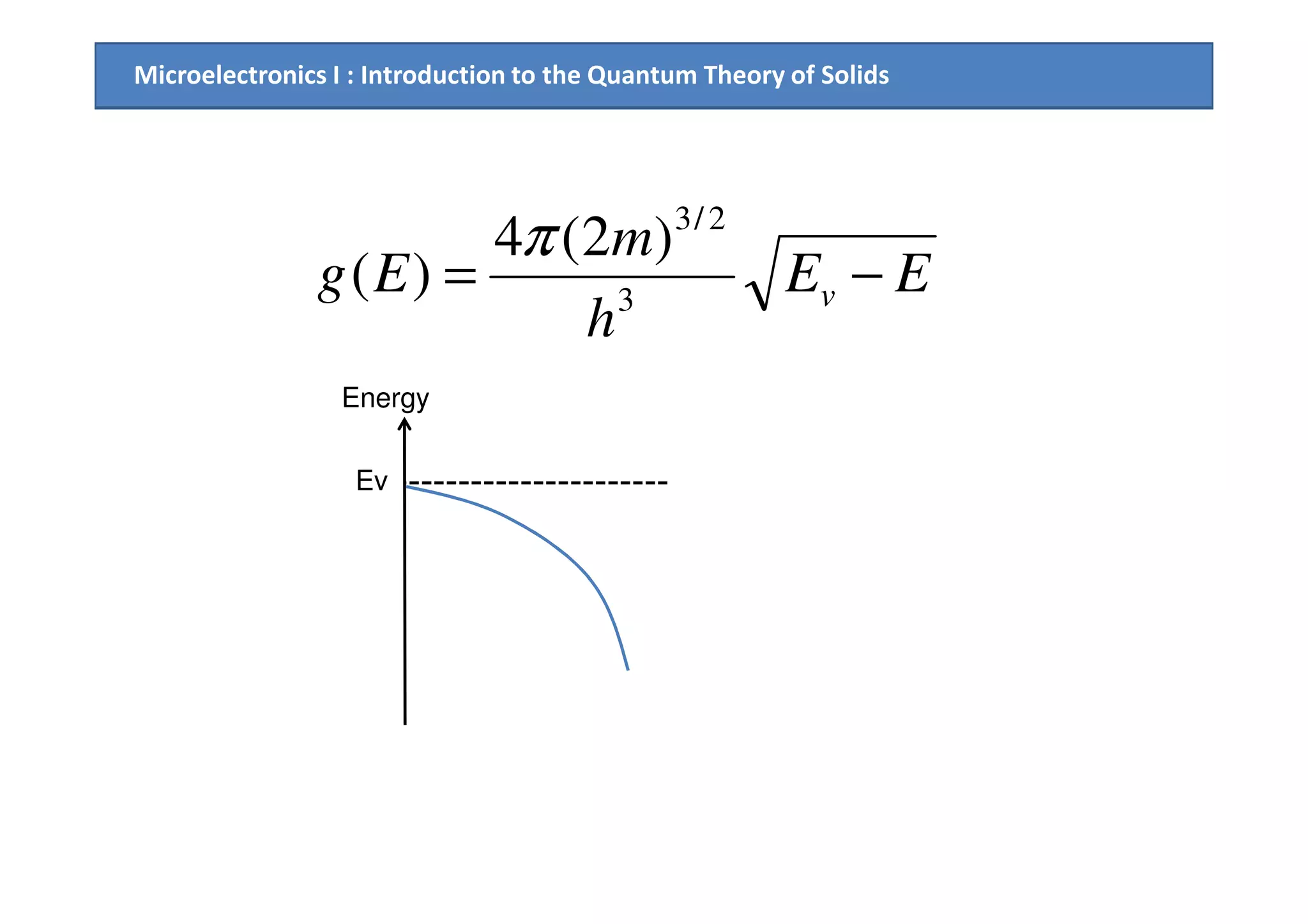
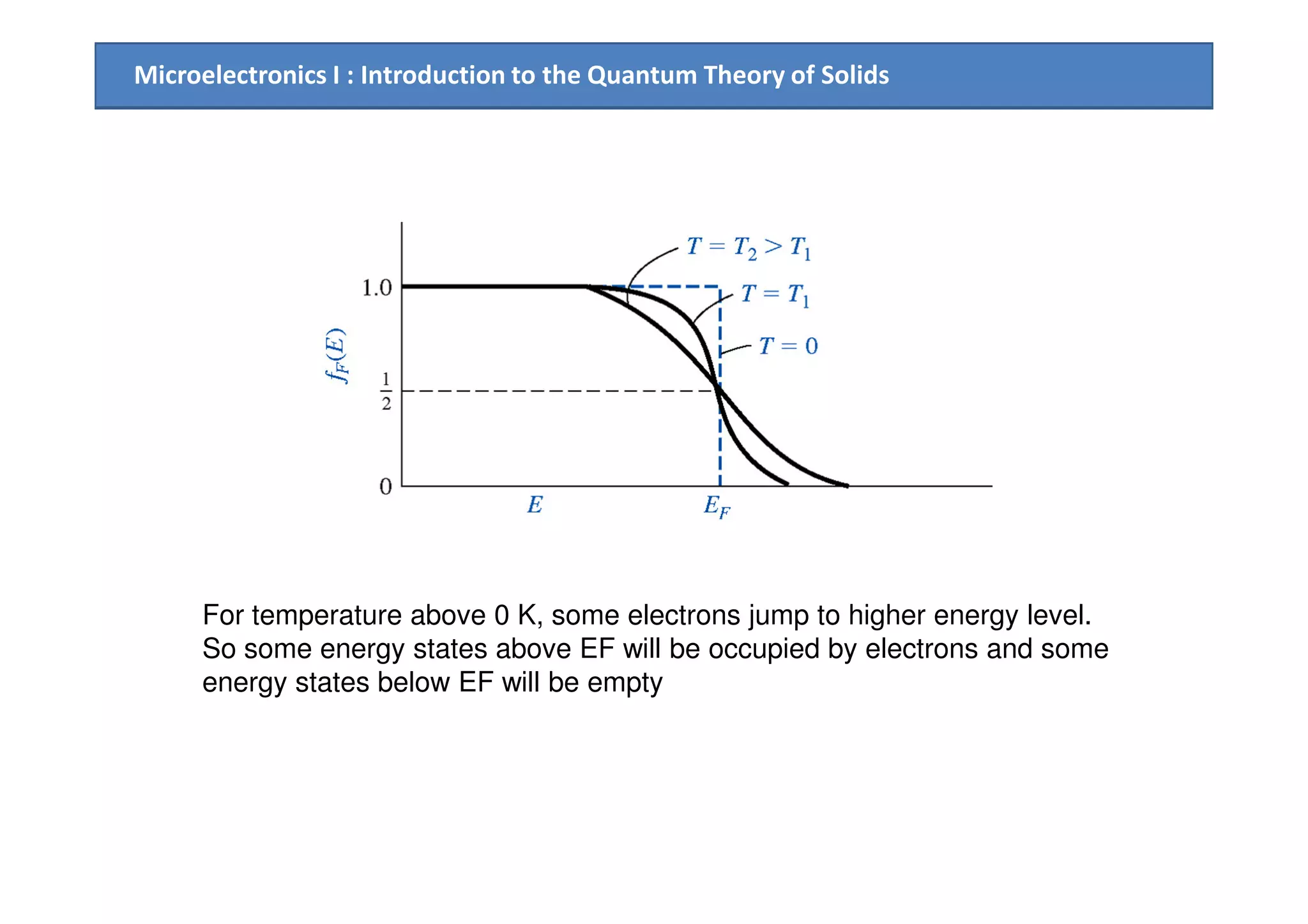
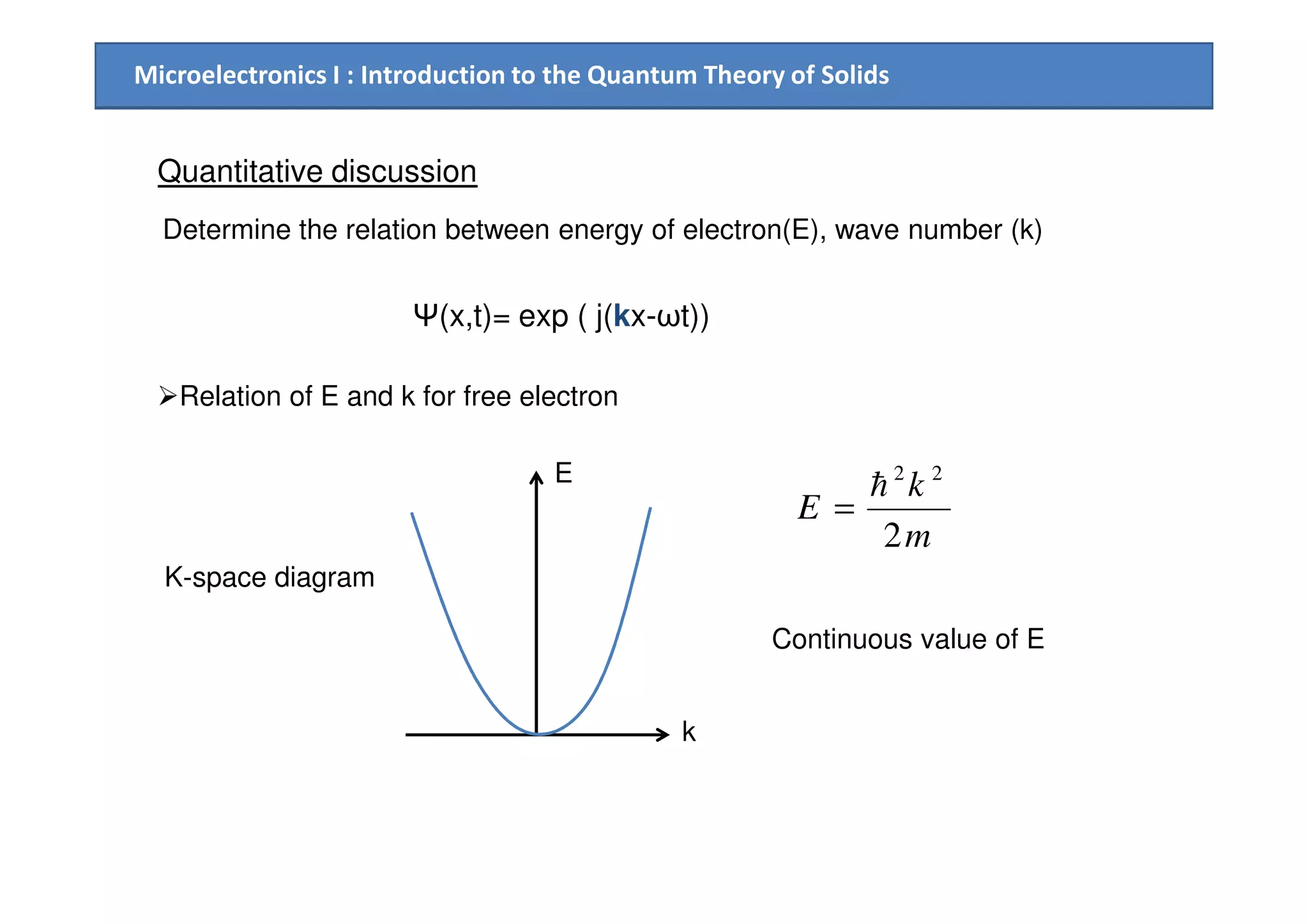
The document provides an introduction to the quantum theory of solids, including:
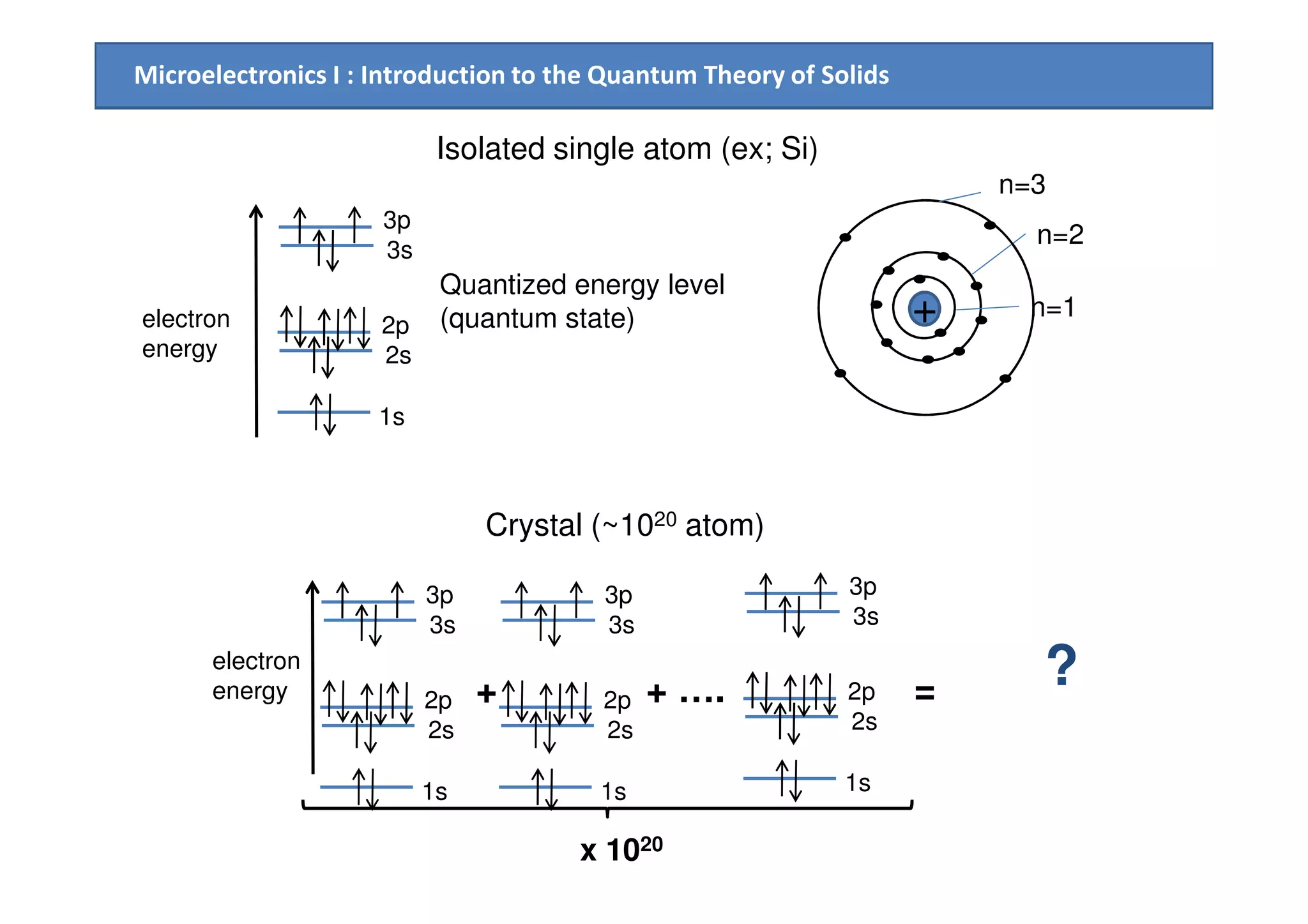
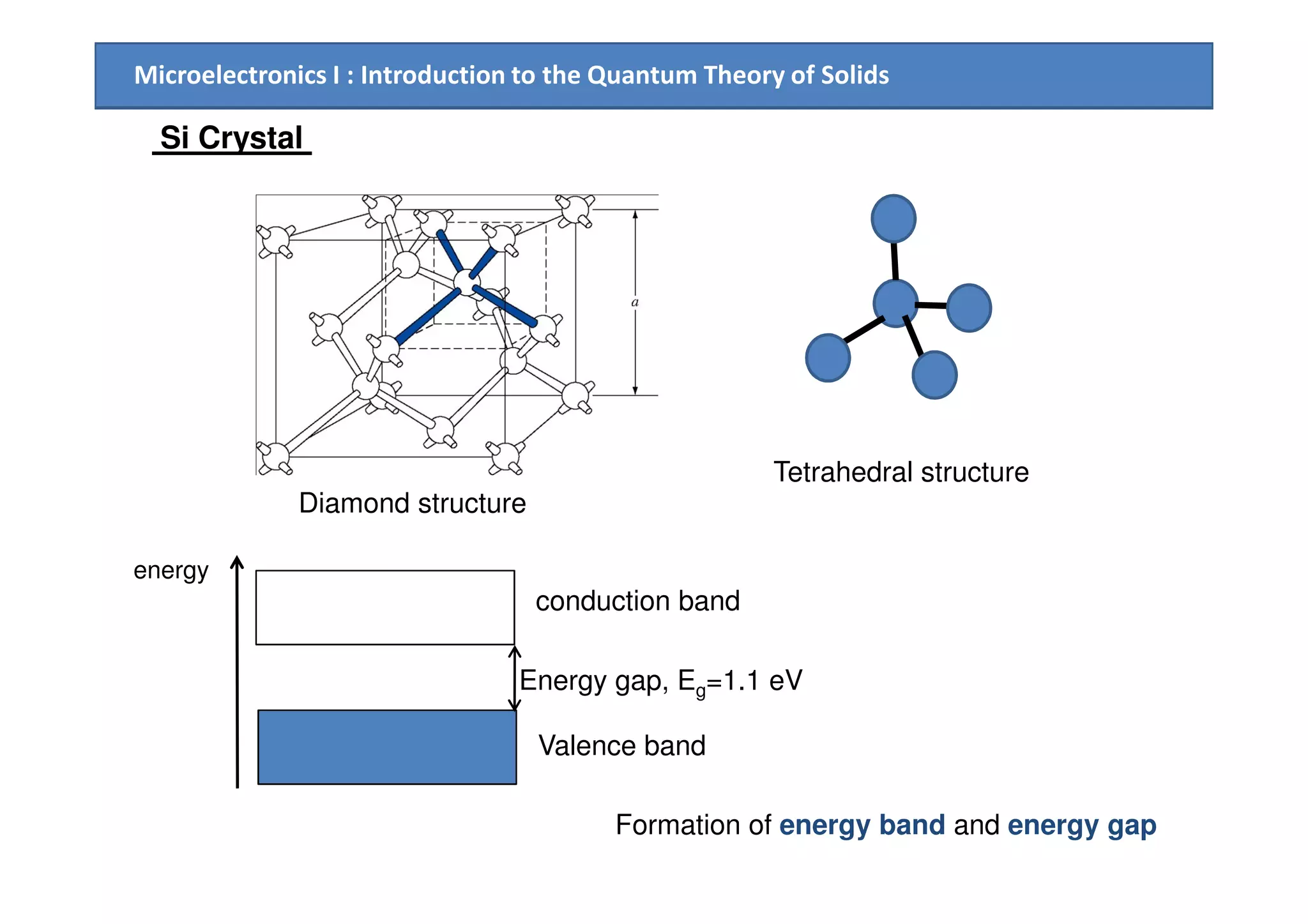
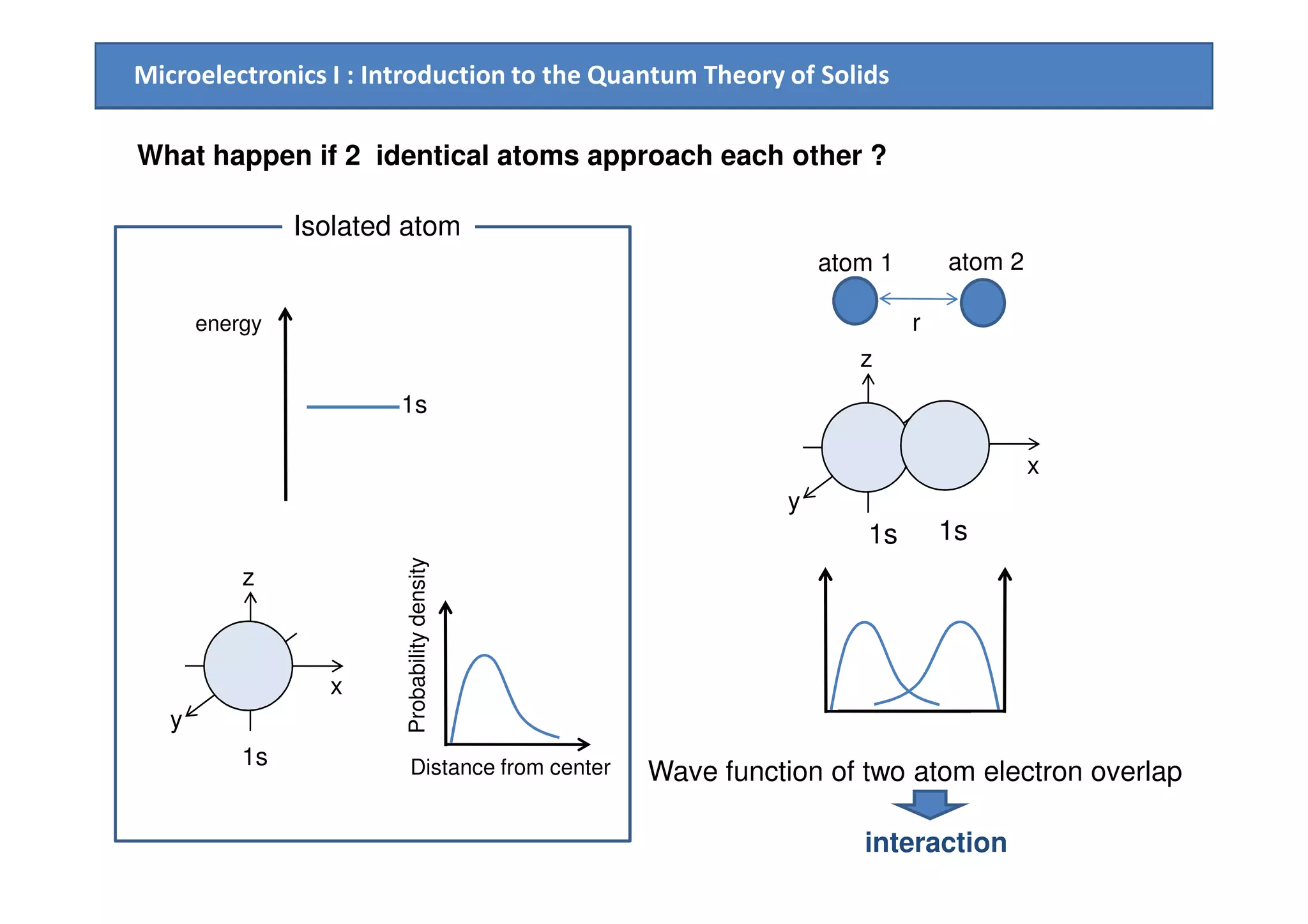
1. How allowed and forbidden energy bands form in solids due to the interaction of atomic electron wave functions when atoms are brought close together in a crystal lattice.
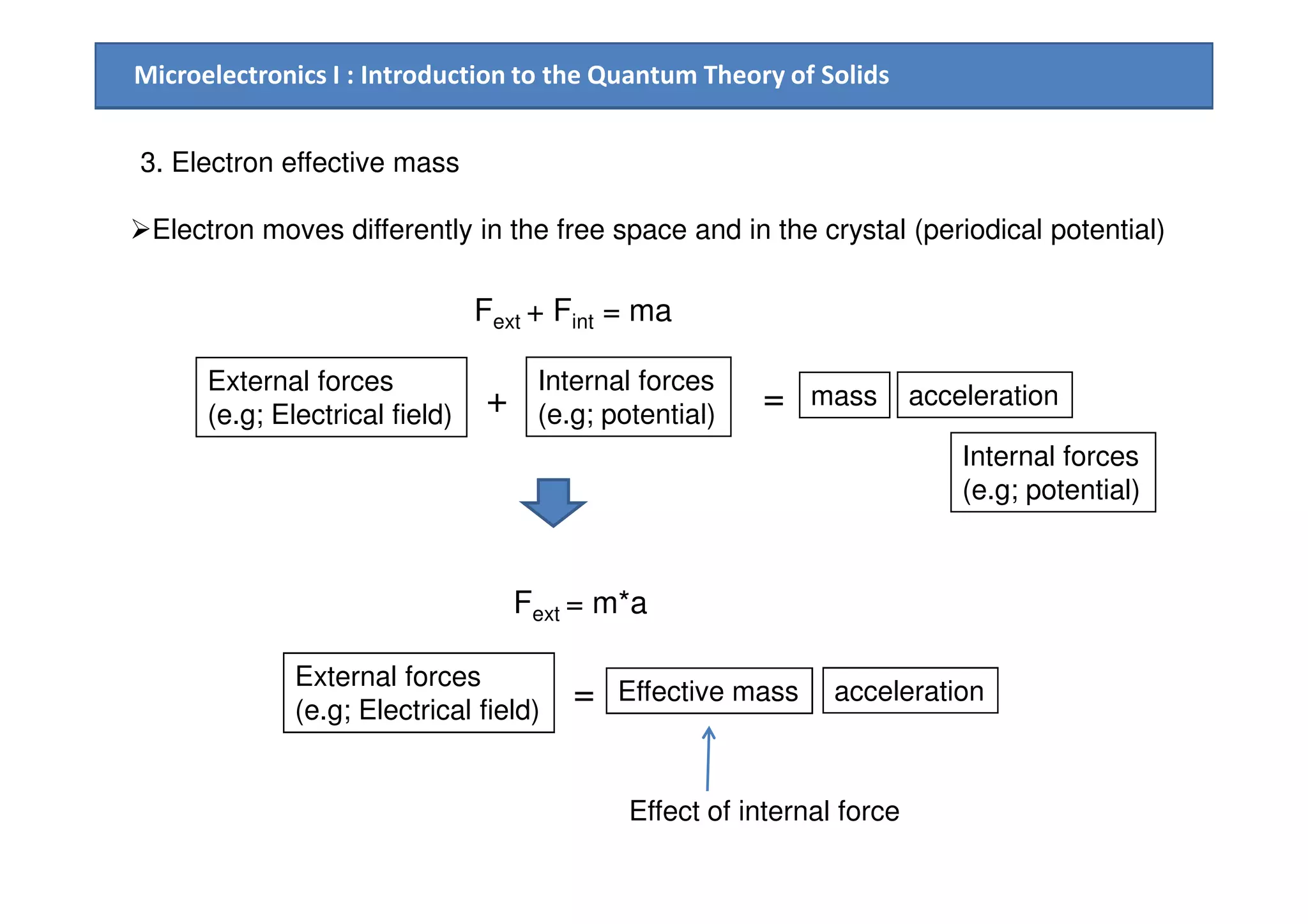
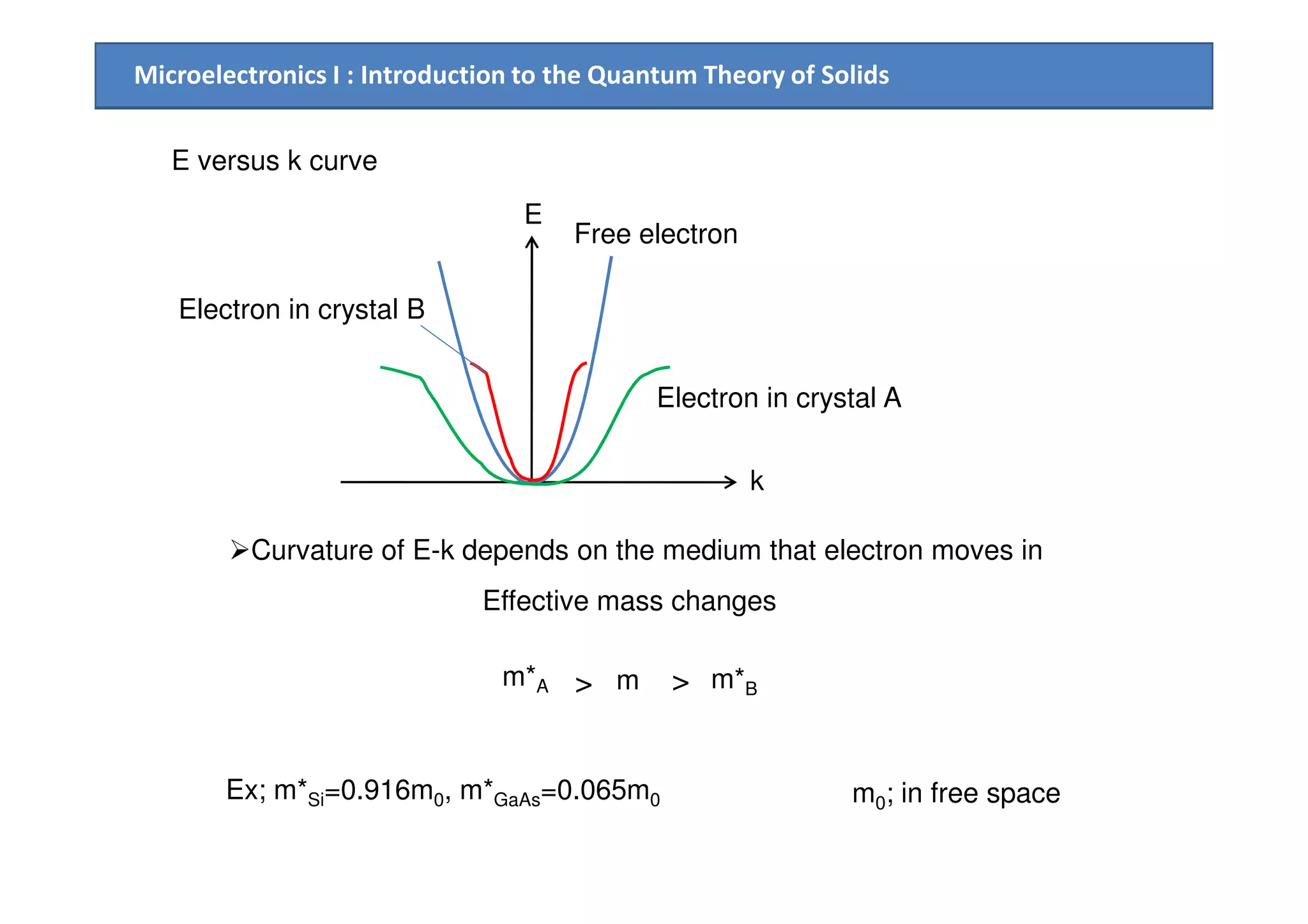
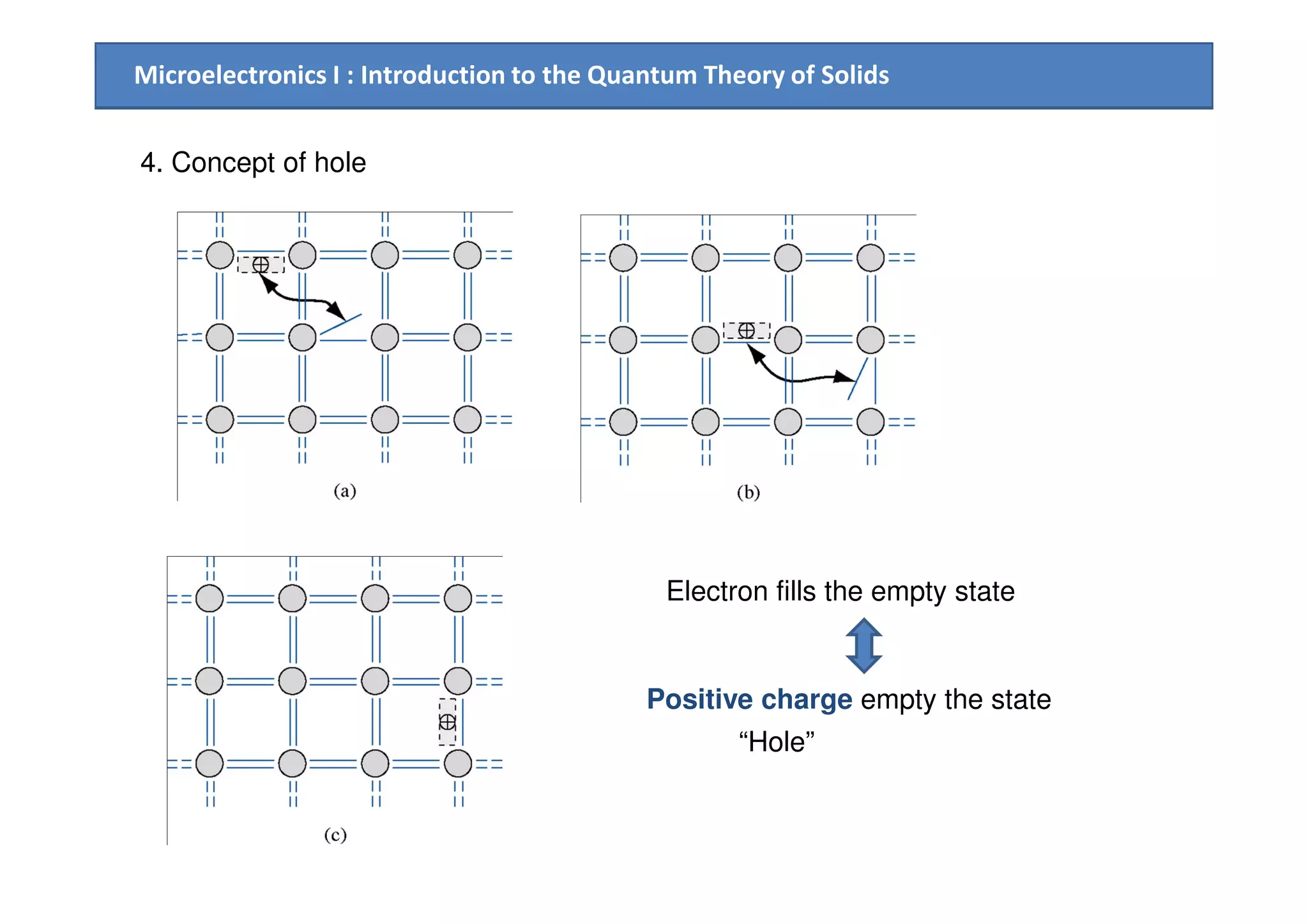
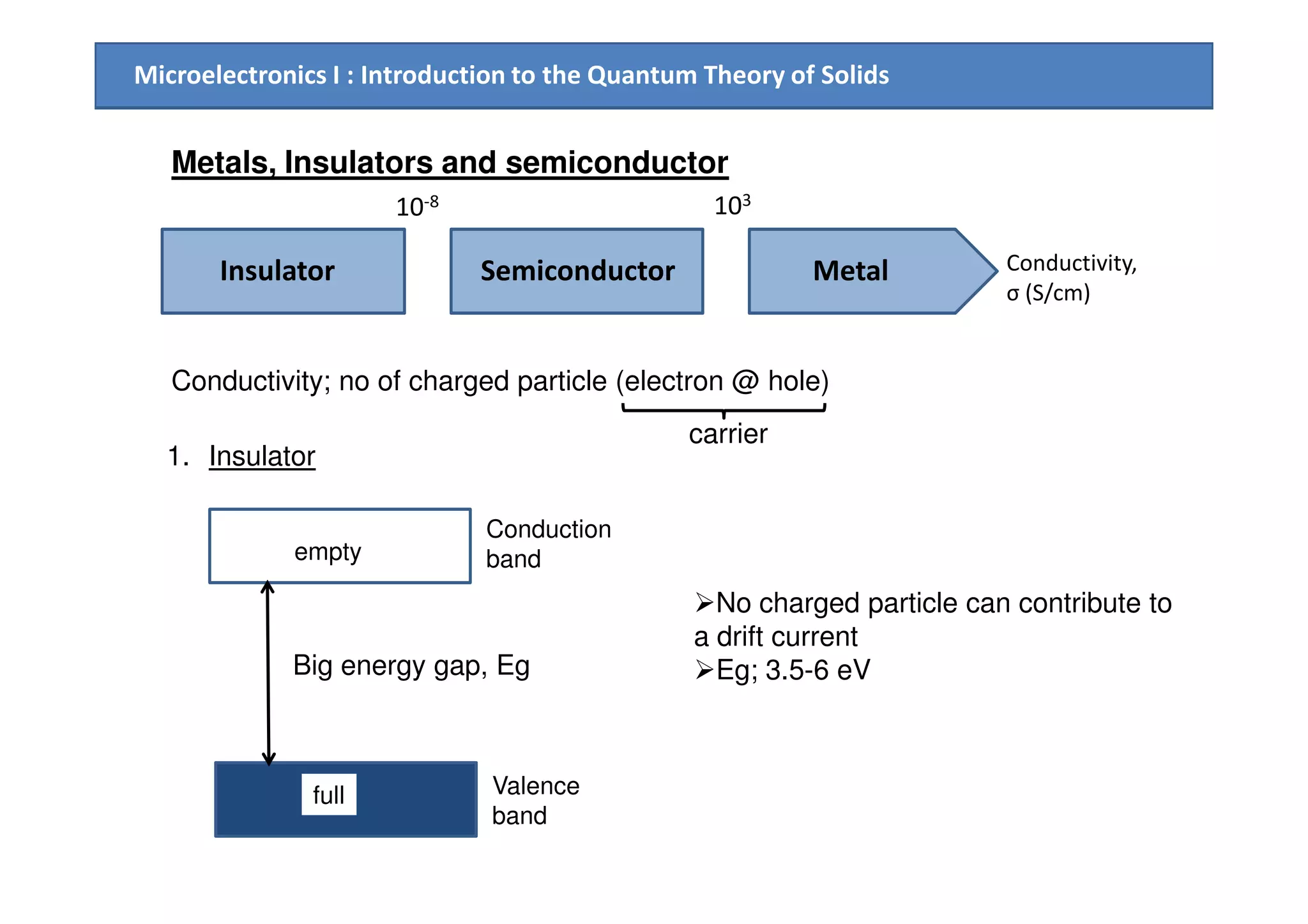
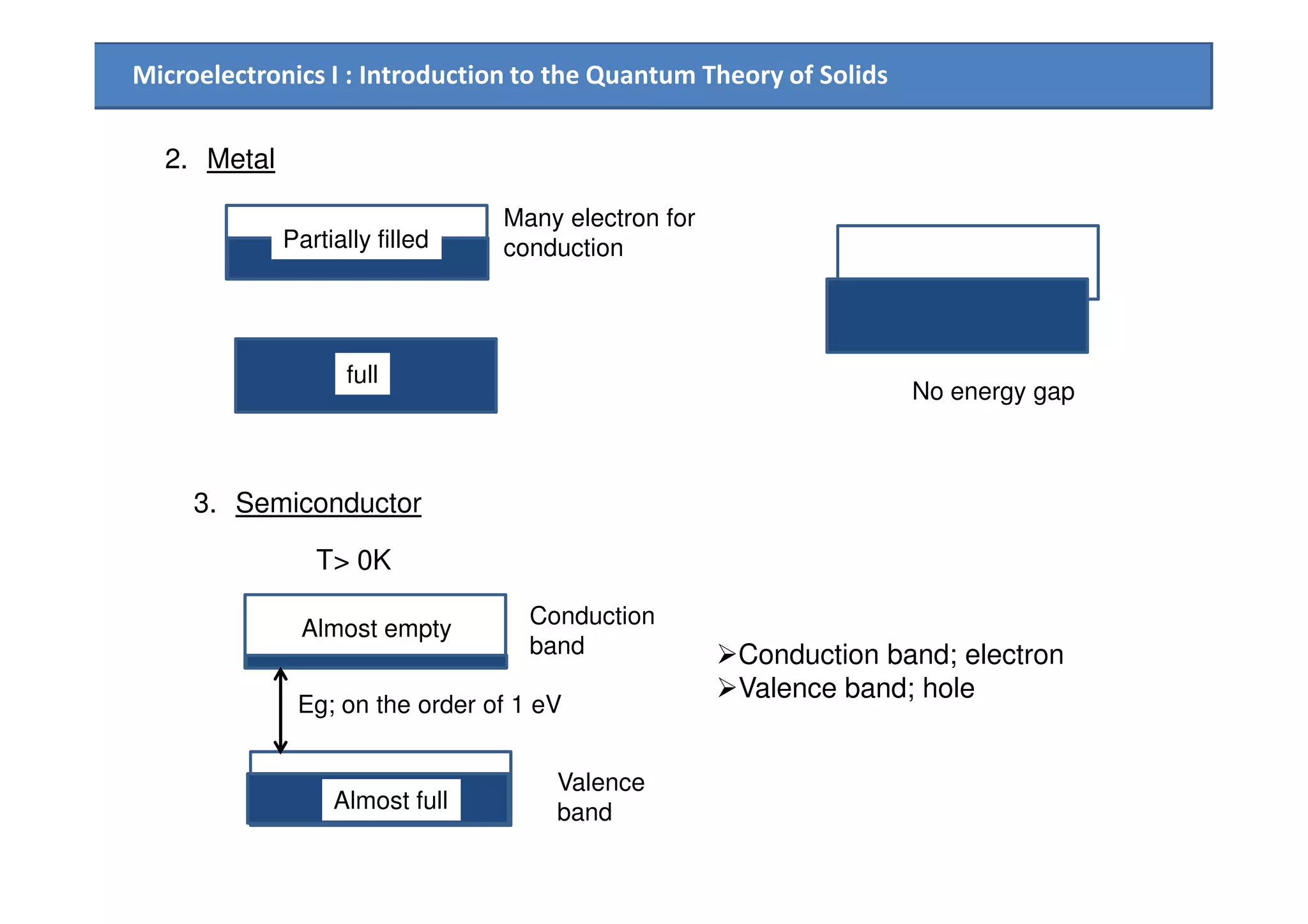
2. Electrical conduction in solids is explained using the concept of electron effective mass and holes, within the framework of the energy band model.
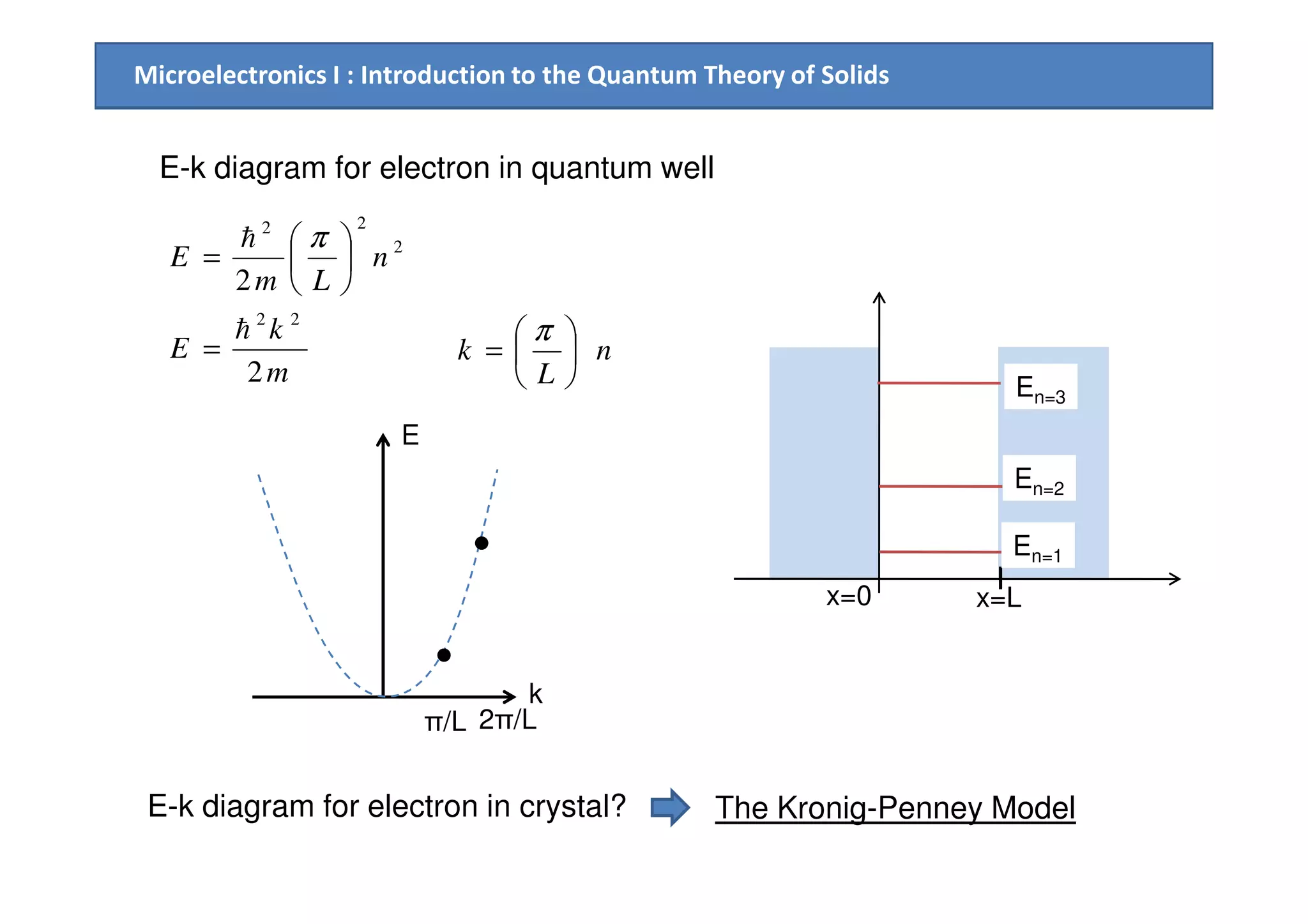
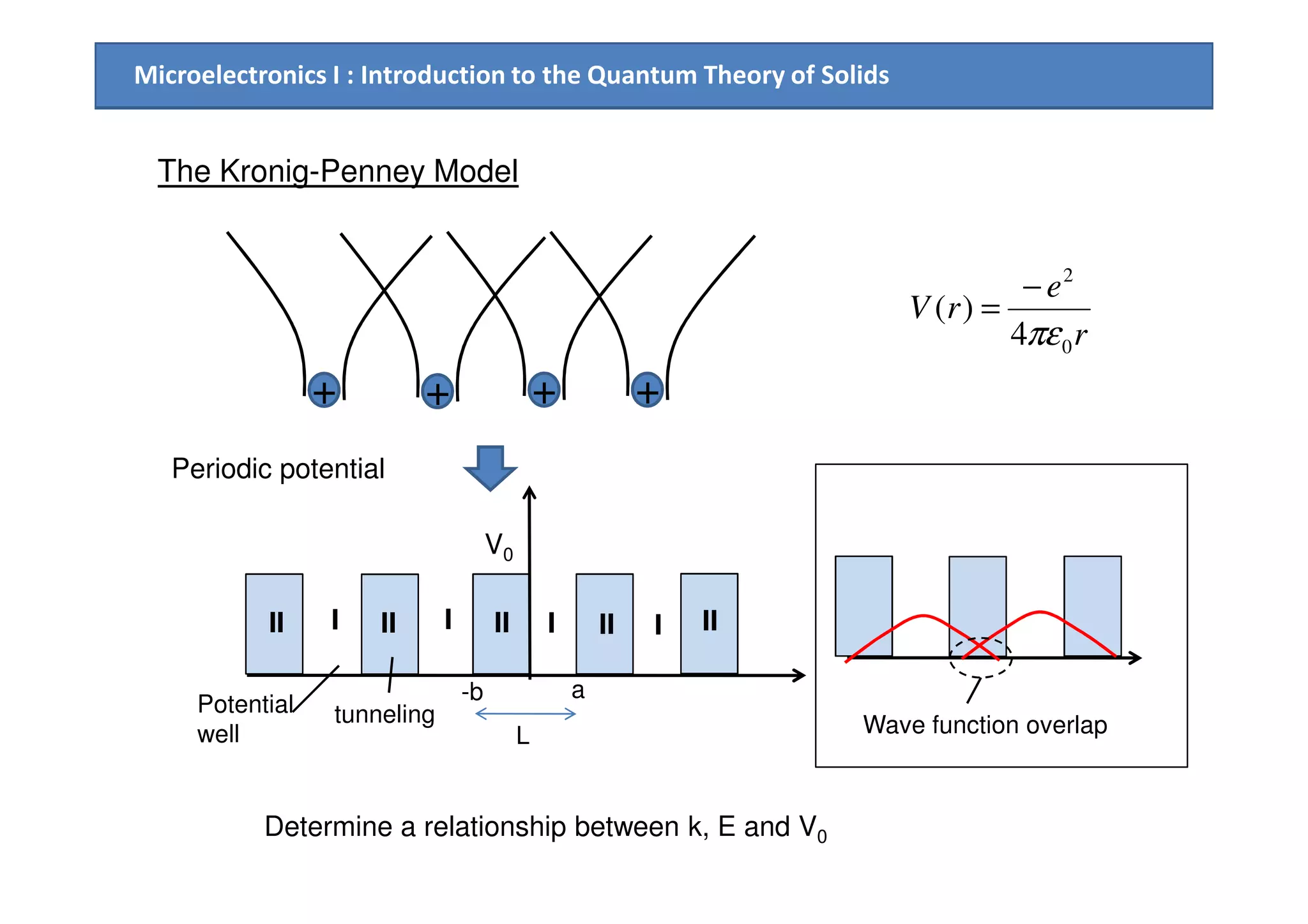
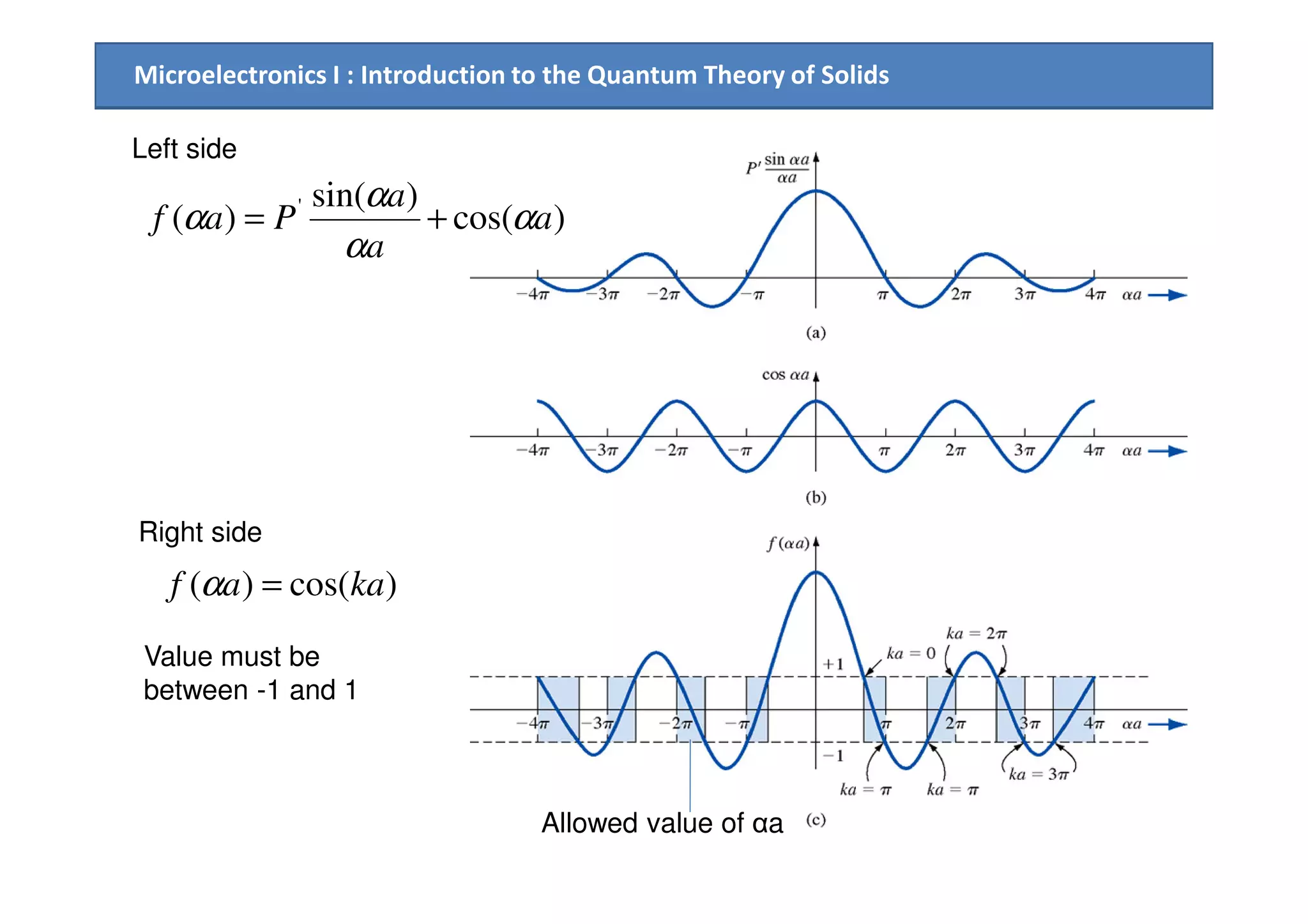
3. The Kronig-Penney model is used to quantitatively relate the energy, wave number, and periodic potential within a solid, resulting in allowed and forbidden energy bands.


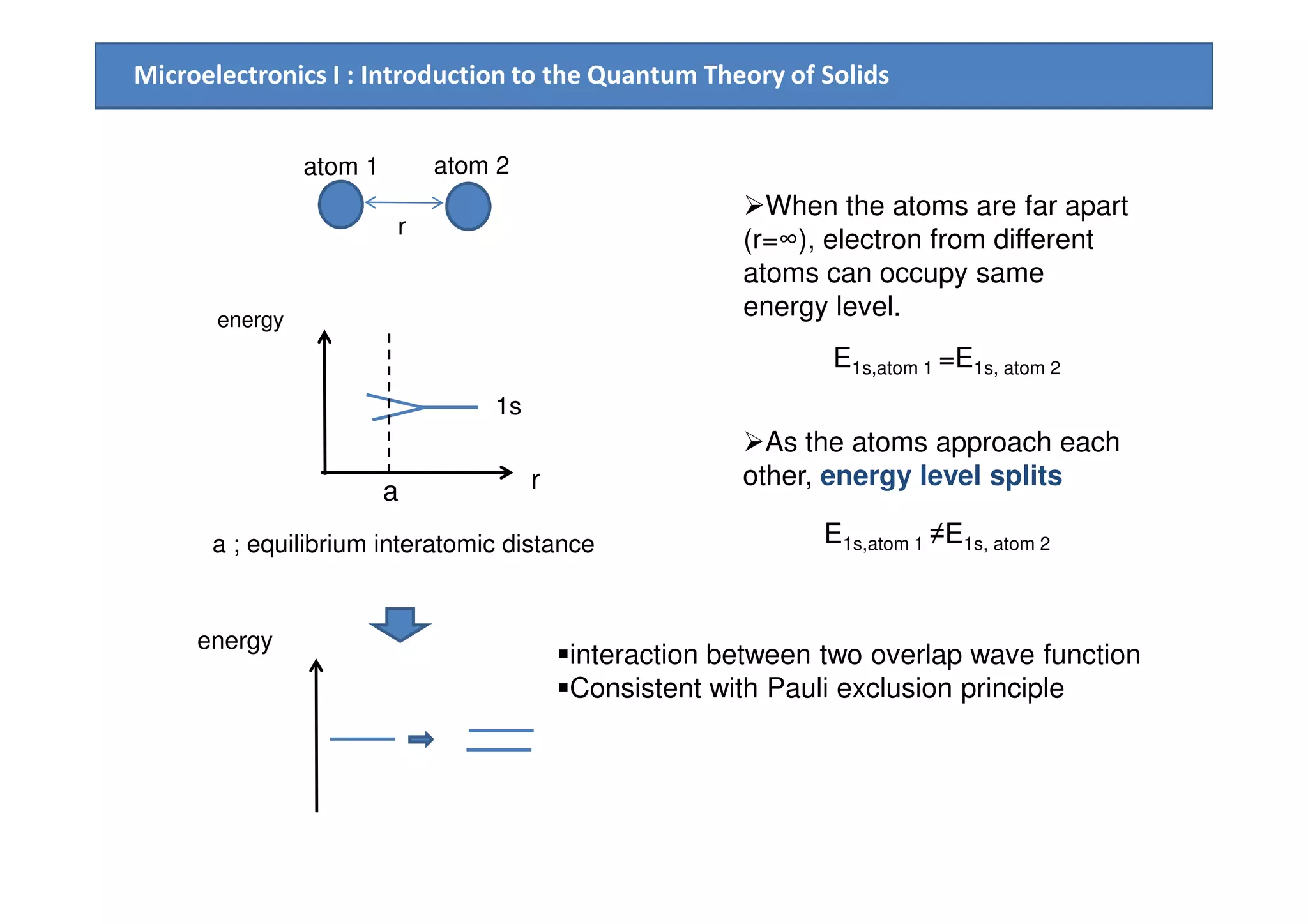
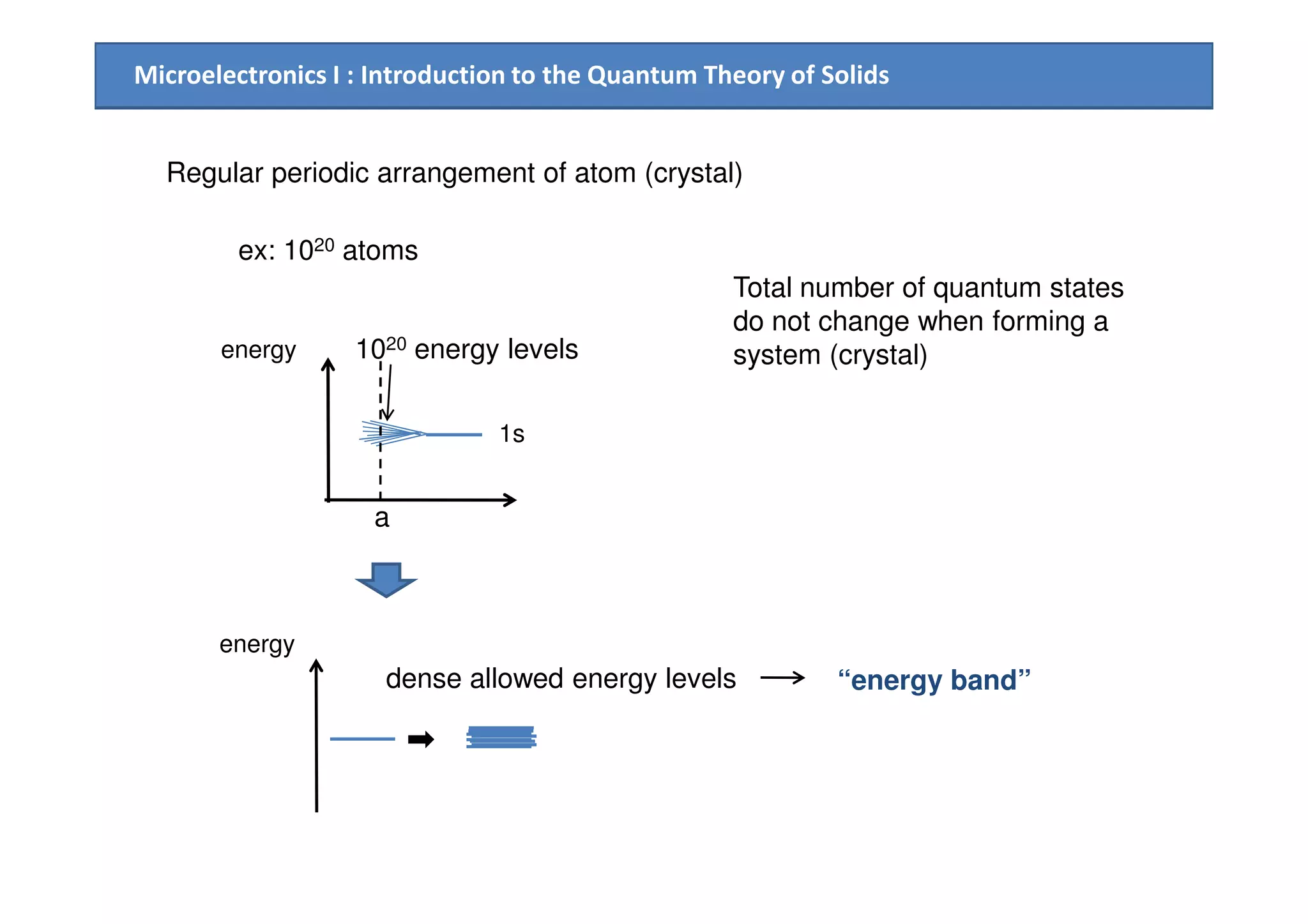
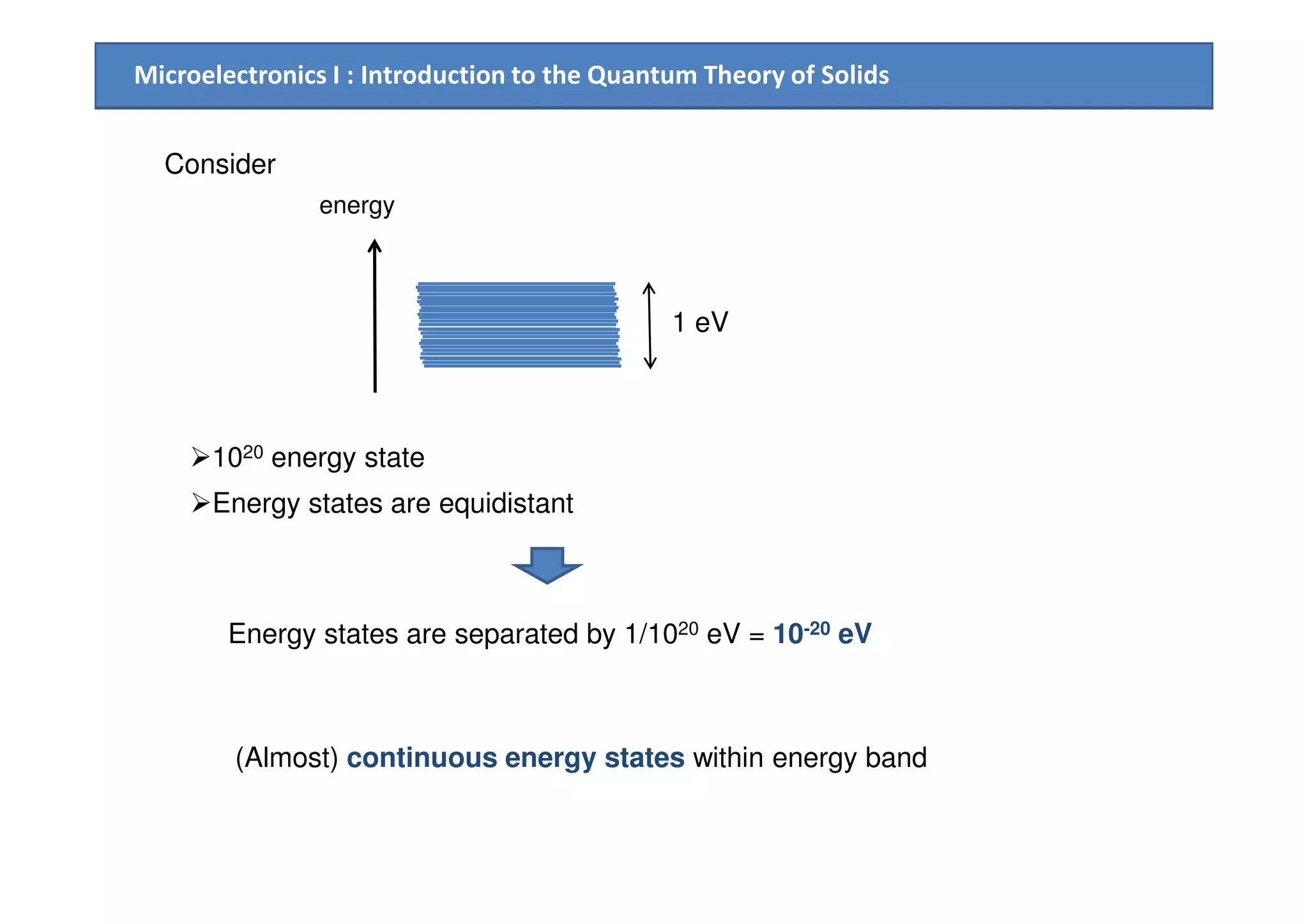
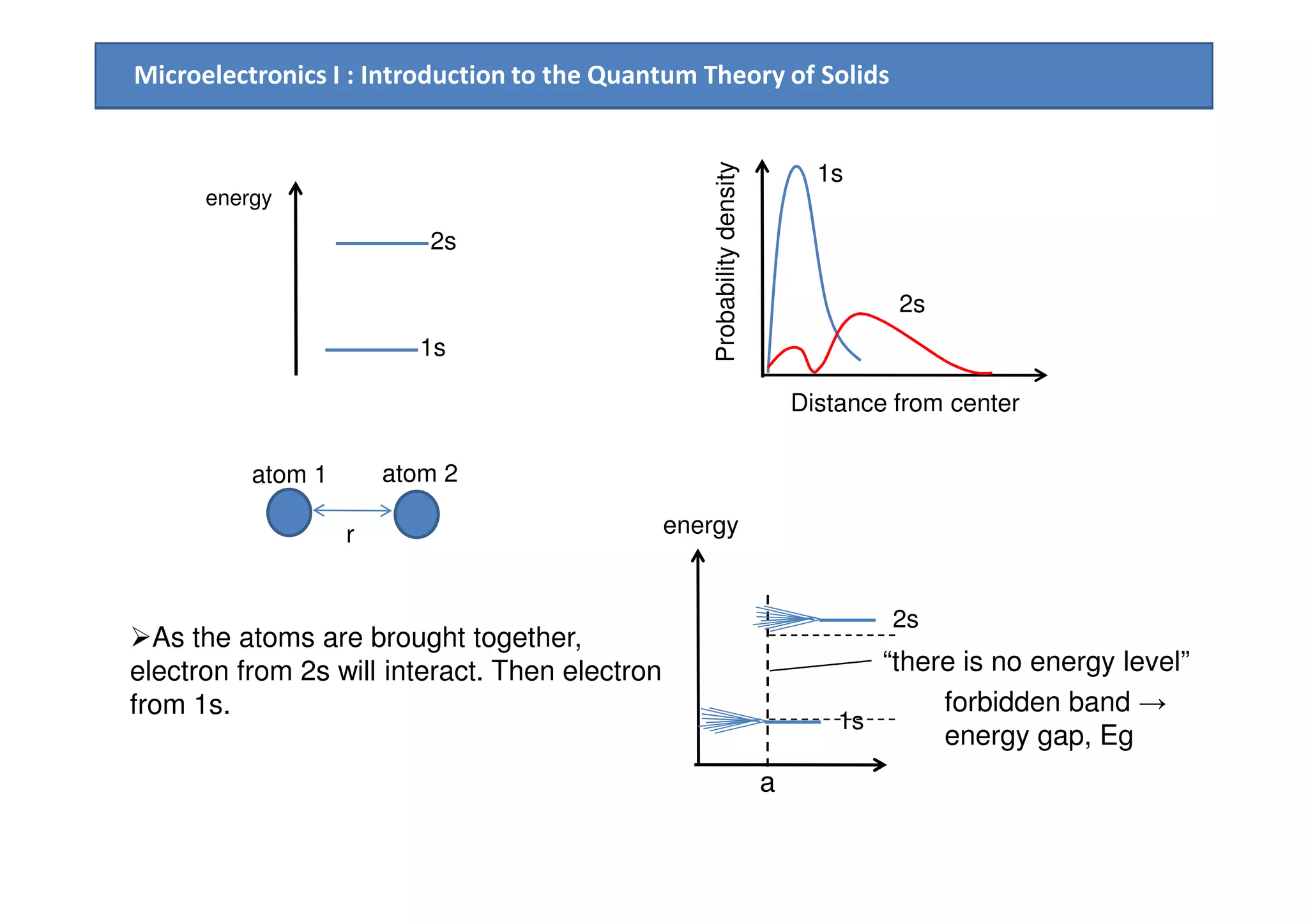
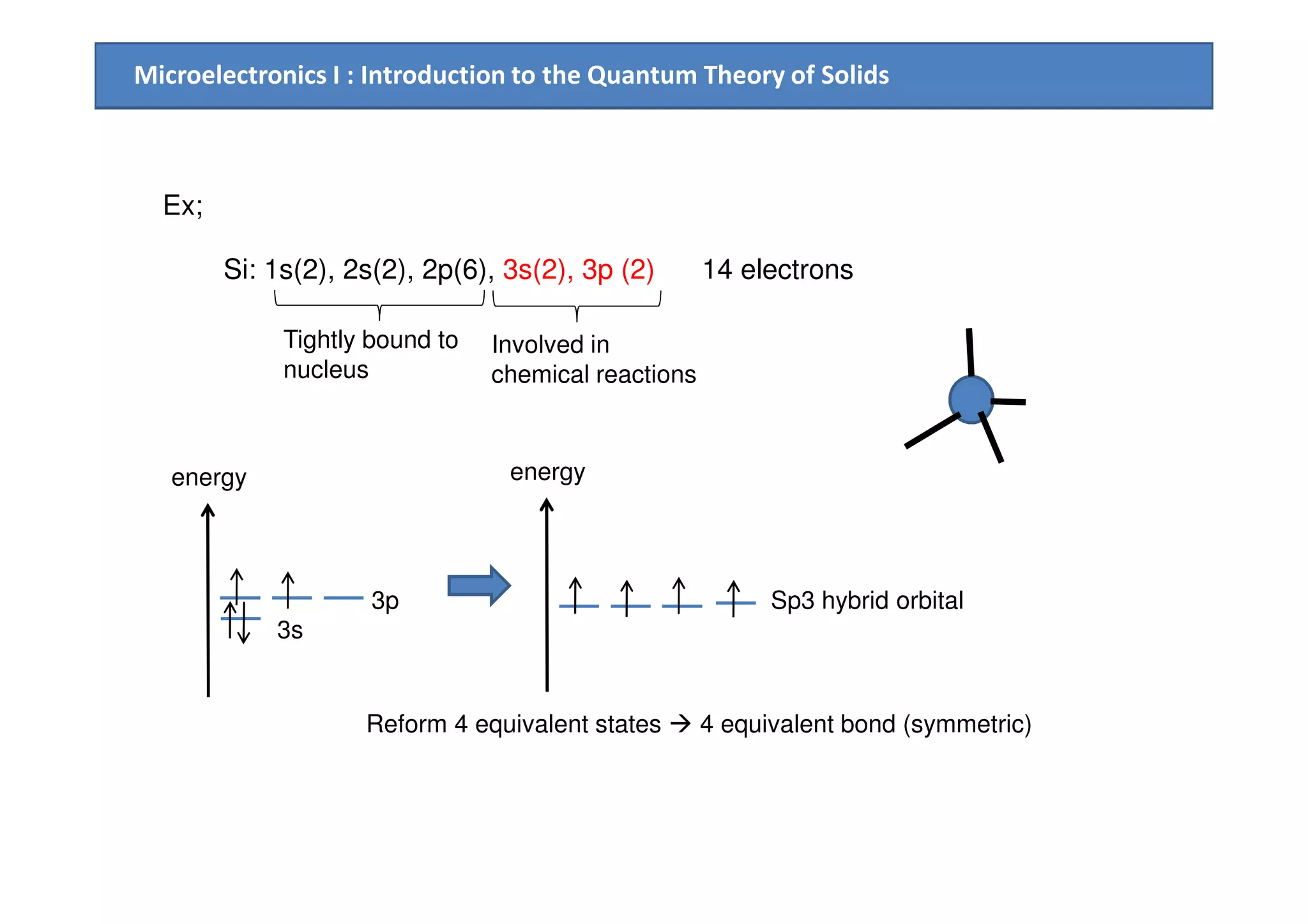
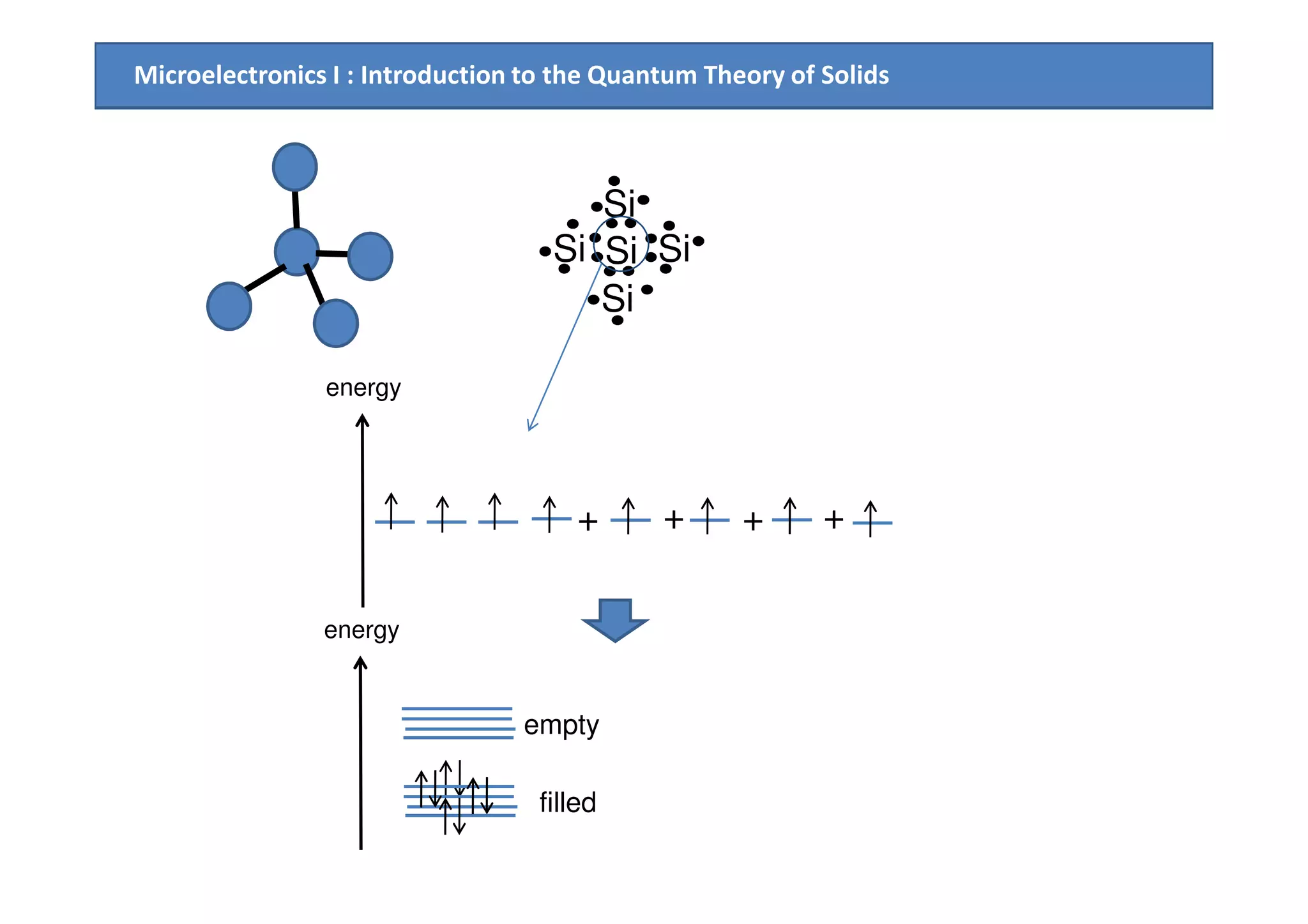
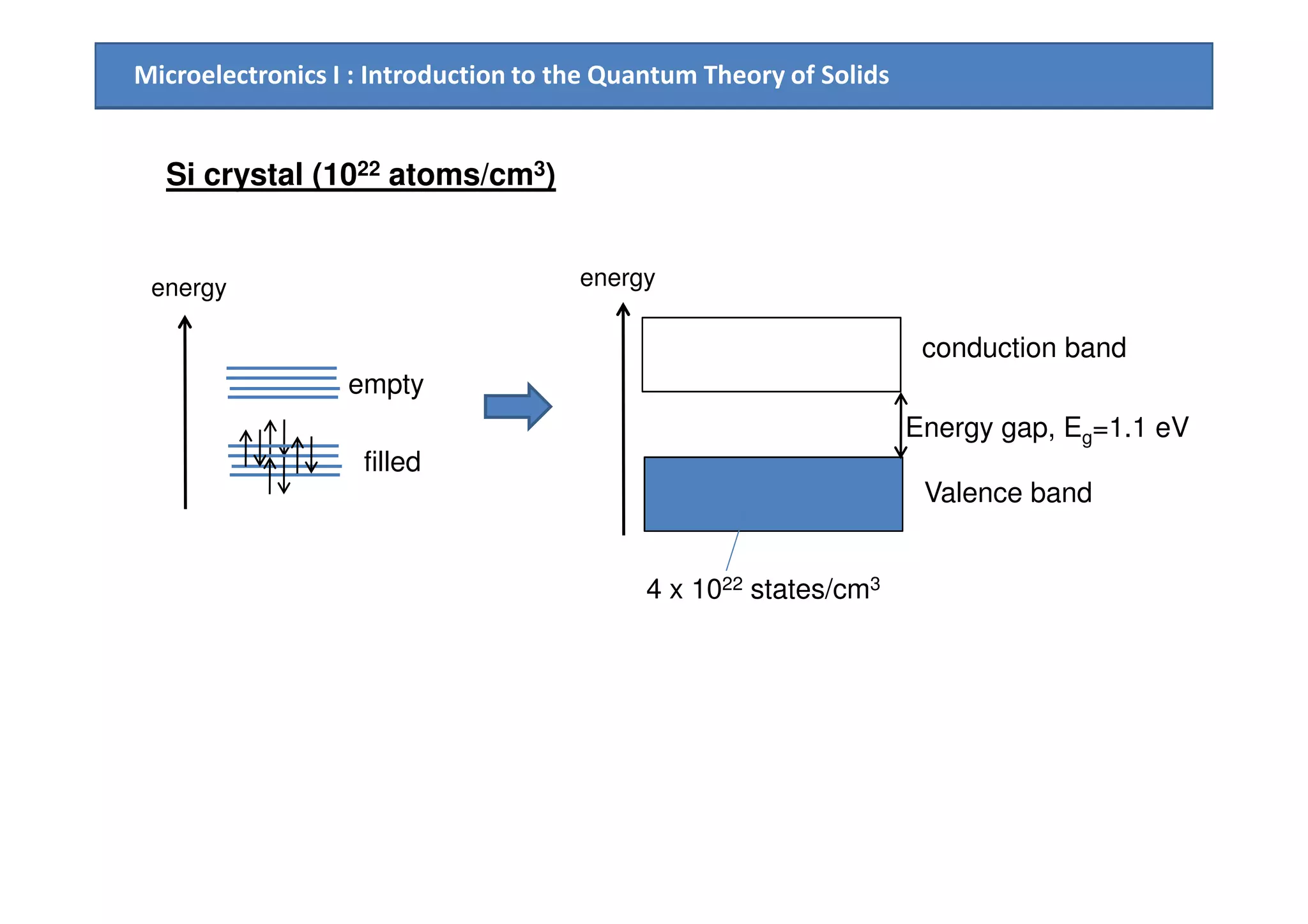
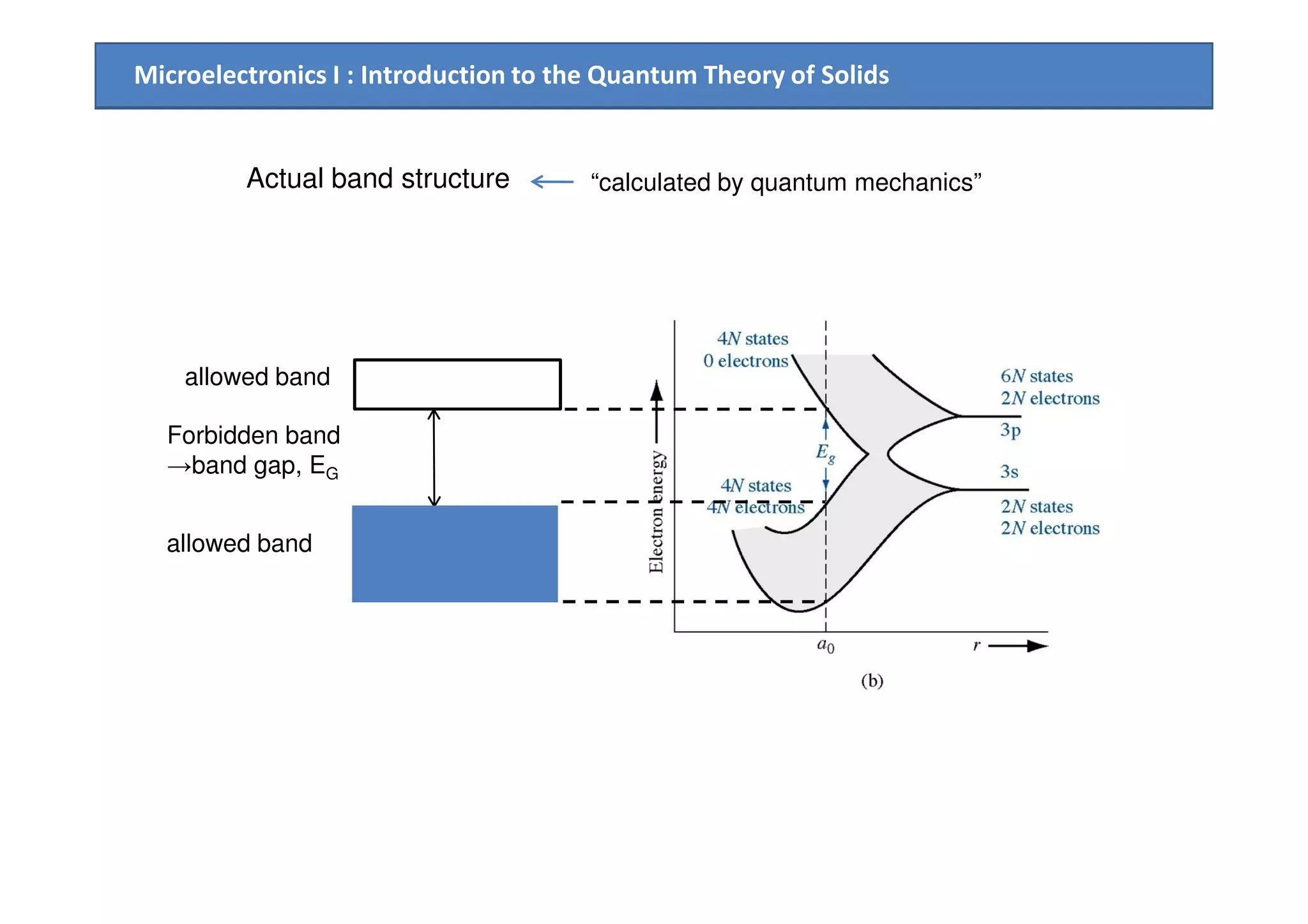
![Microelectronics I : Introduction to the Quantum Theory of Solids
Schrodinger equation (E < V0)
Region I 0)(
)( 2
2
2
=+
∂
∂
x
x
x
I
I
ϕα
ϕ
Region II 0)(
)( 2
2
2
=−
∂
∂
x
x
x
II
II
ϕβ
ϕ
2
2 2
h
mE
=α
2
02 )(2
h
EVm −
=β
Potential periodically changes
)()( LxVxV +=
jkx
exUx )()( =ϕ
)()( LxUxU +=
Wave function
amplitude
k; wave number [m-1]
Phase of the wave
Bloch theorem](https://image.slidesharecdn.com/chapter3introductiontothequantumtheoryofsolids-161210152458/75/Chapter3-introduction-to-the-quantum-theory-of-solids-17-2048.jpg)


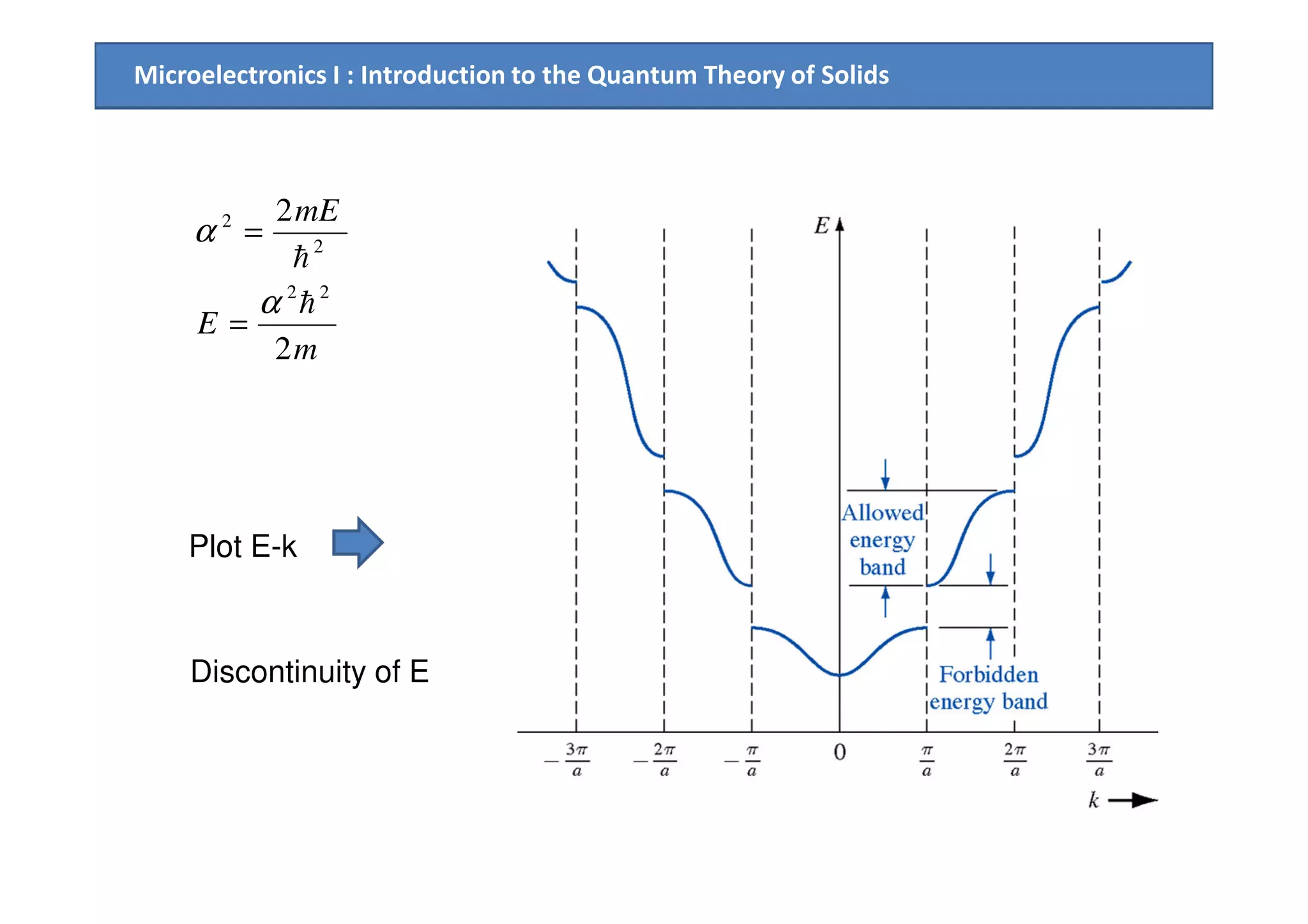
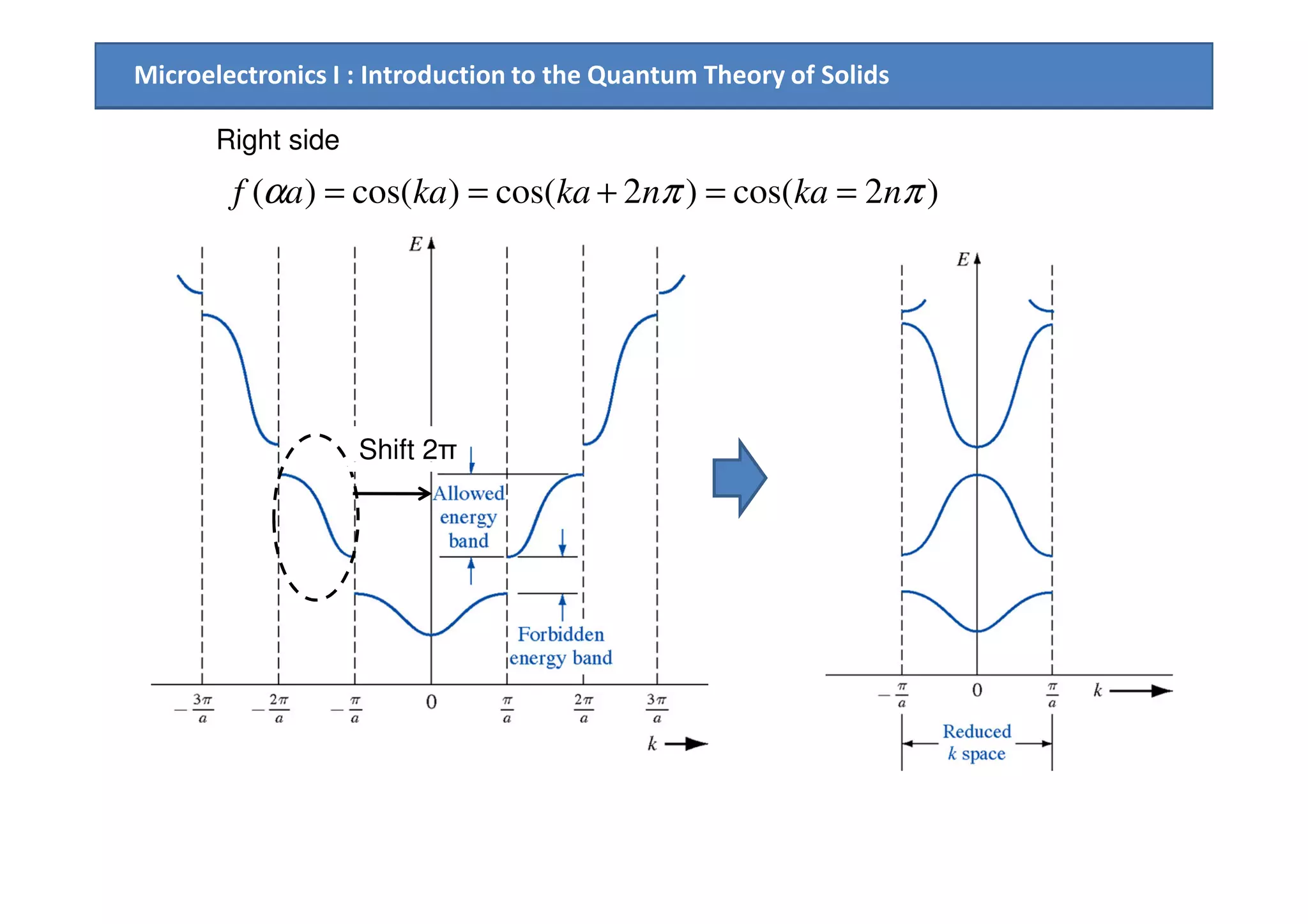
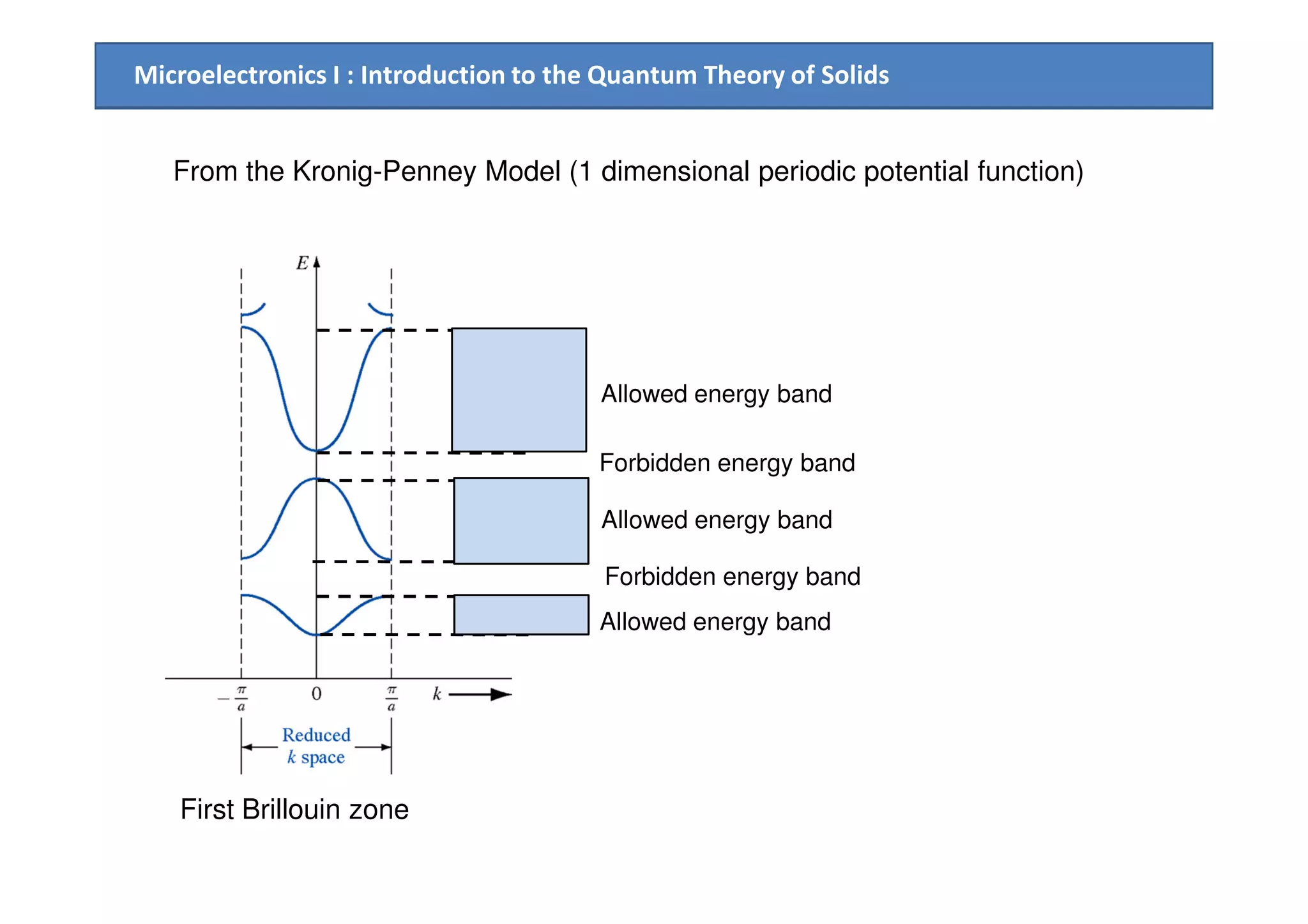
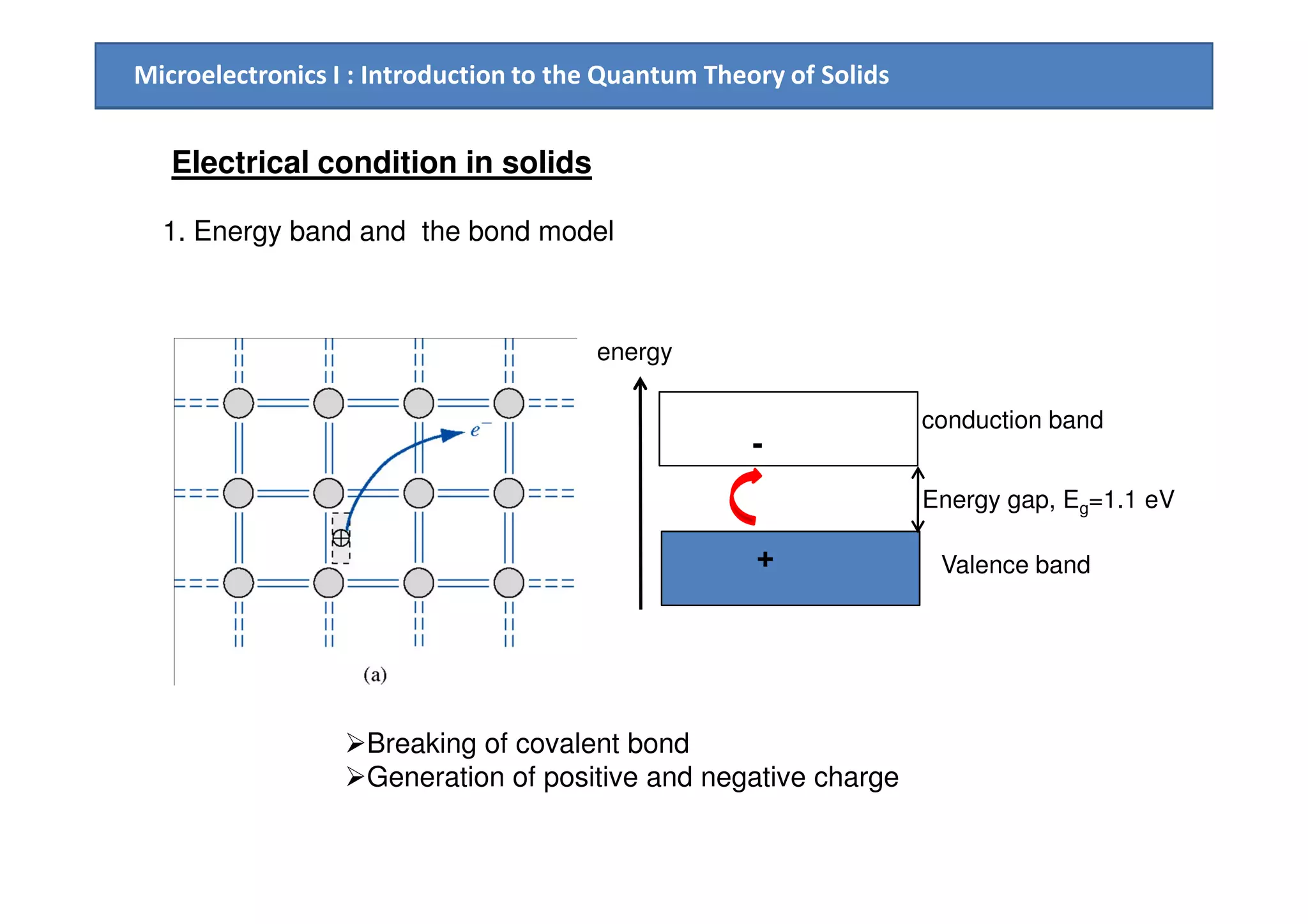
![Microelectronics I : Introduction to the Quantum Theory of Solids
2. Drift current
Current; diffusion current and drift current
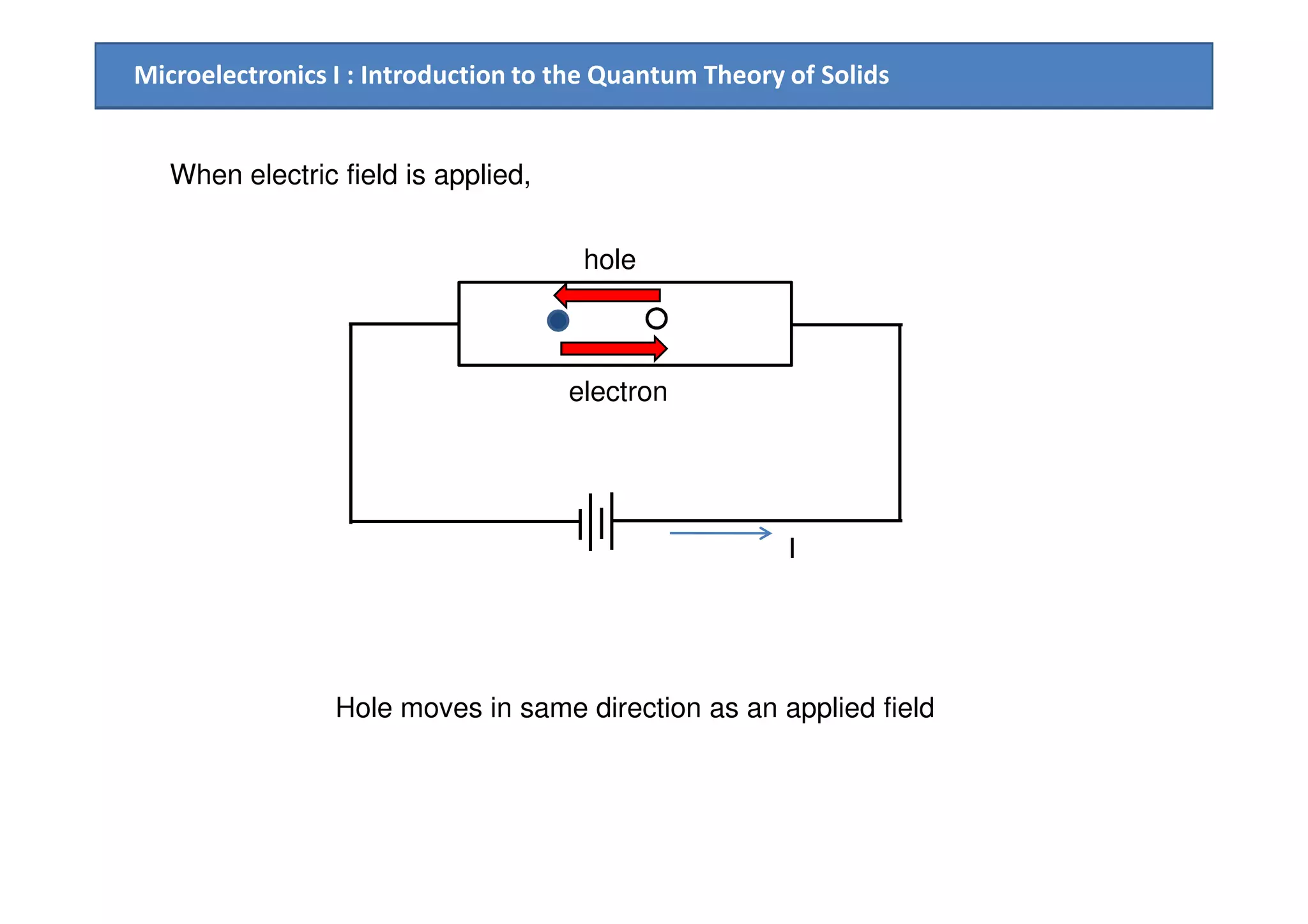
When Electric field is applied
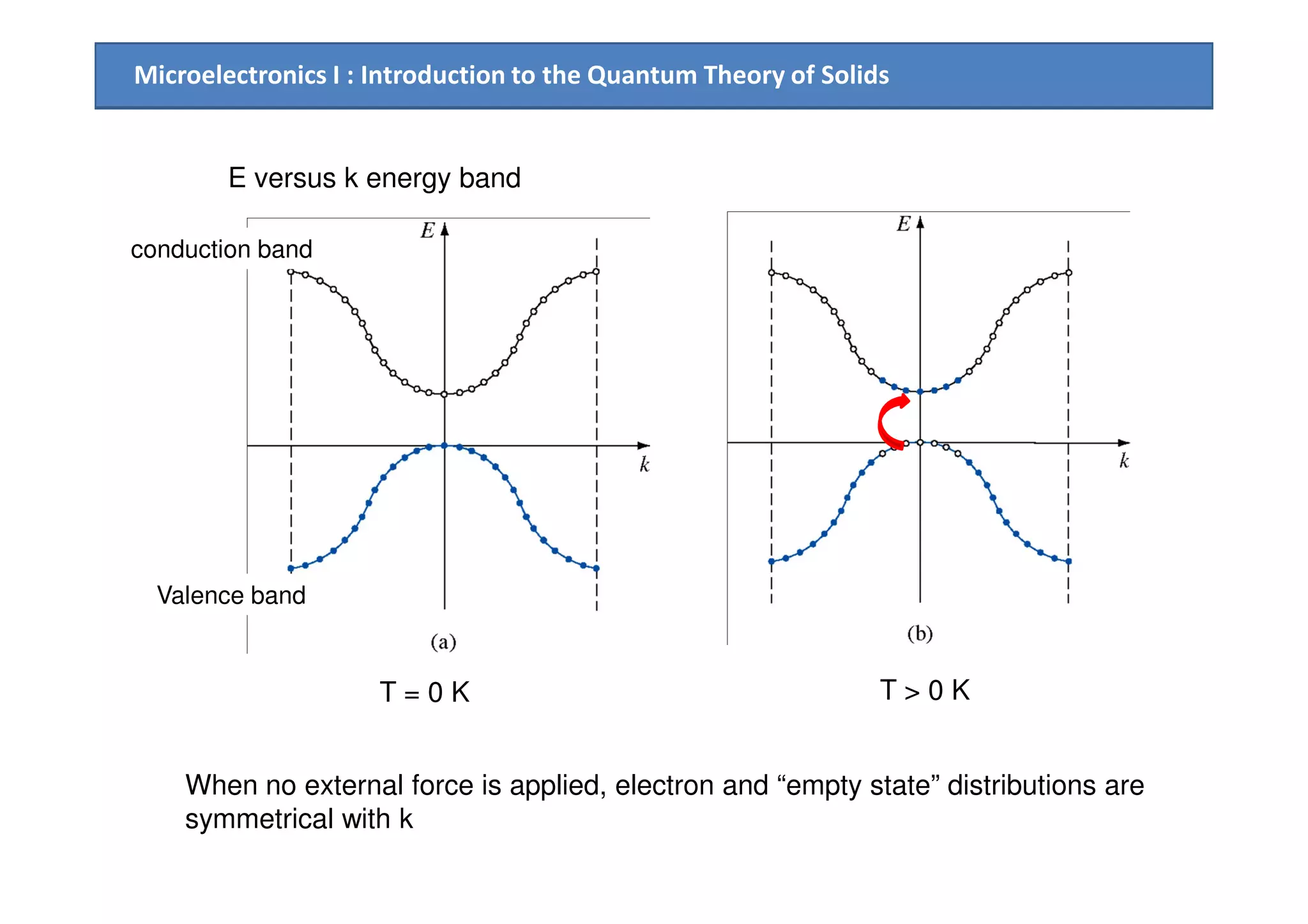
E E
dE = F dx = F v dt
“Electron moves to higher empty state”
k k
ENo external force
∑=
υ−=
n
i
ieJ
1
Drift current density, [A/cm3]
n; no. of electron per unit volume in the conduction band](https://image.slidesharecdn.com/chapter3introductiontothequantumtheoryofsolids-161210152458/75/Chapter3-introduction-to-the-quantum-theory-of-solids-26-2048.jpg)

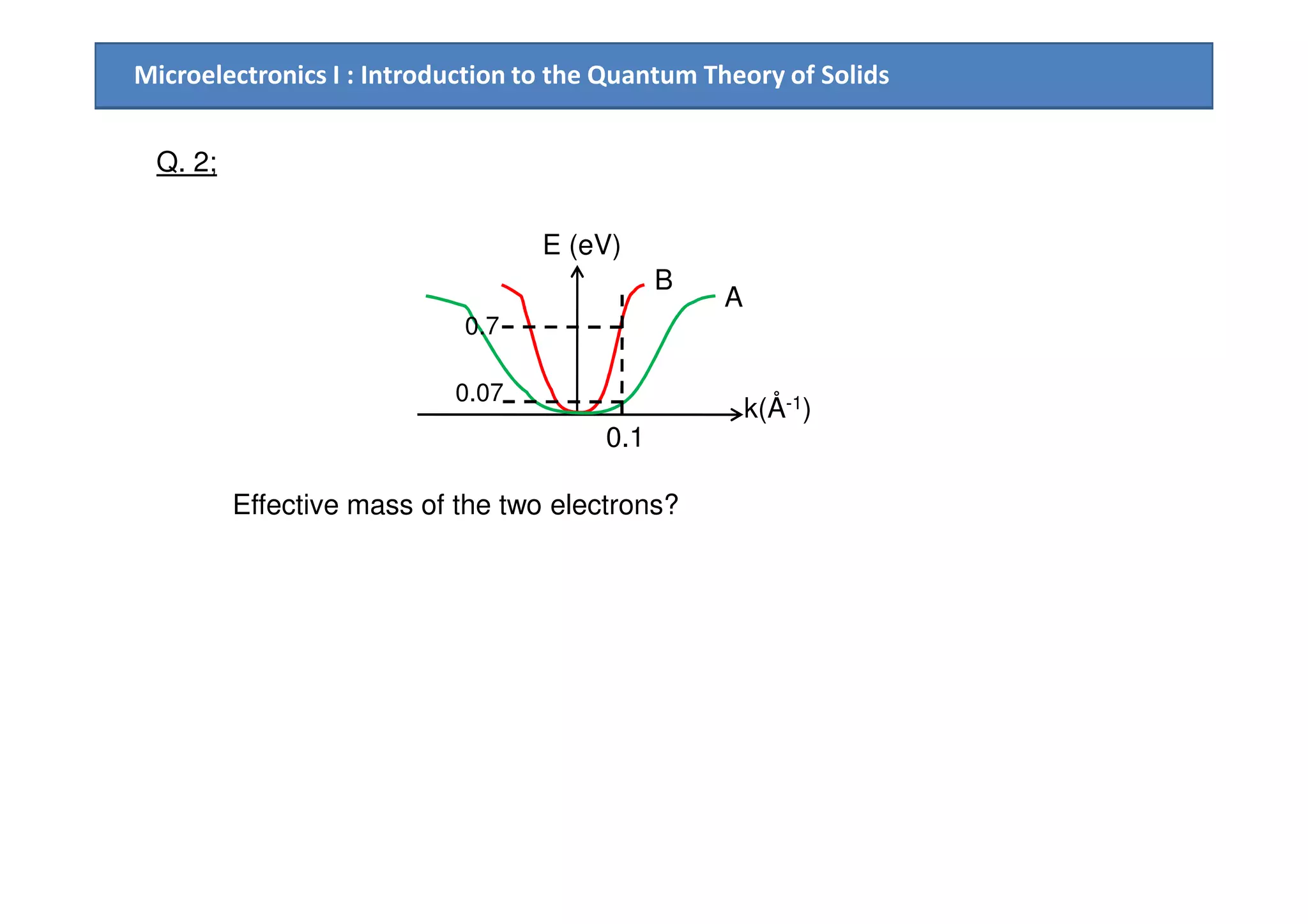
![Microelectronics I : Introduction to the Quantum Theory of Solids
Extension to three dimensions
[110]
1 dimensional model (kronig-Penney Model)
1 potential pattern
[100]
direction
[110]
direction
Different direction
Different potential patterns
E-k diagram is given by a function of the direction in the crystal](https://image.slidesharecdn.com/chapter3introductiontothequantumtheoryofsolids-161210152458/75/Chapter3-introduction-to-the-quantum-theory-of-solids-36-2048.jpg)