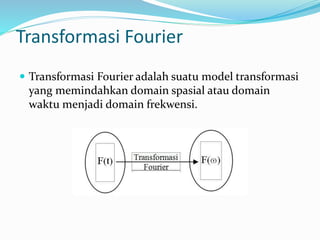
Dokumen ini membahas tentang deret Fourier, transformasi Fourier, dan aplikasinya dalam analisis sinyal. Transformasi Fourier memindahkan data dari domain waktu ke domain frekuensi, dengan kelebihan dan kekurangan dalam hal analisis sinyal. Selain itu, dijelaskan juga tentang bilangan kompleks yang penting dalam pemrosesan sinyal digital.

1. Kelompok 5 :
Imay Willian Perdana (5150711094)
Aditya Pratama (5150711054)
Rohman Iskandar (5150711078)
Regy Buana Pramana (5150711074)
Alan Zarkasi (5150711085)
Danang Dwi Prasetya (5150711062)

2. Deret Fourier
 Memiliki fungsi ganjil, genap, da jangkauan setengah.
 Sebuah fungsi dimisalkan f(x)
Bilangan genap berlaku: f(-x)= f(x)
Bilangan ganjil berlaku: f(x)= -f(x)
Misal;
Genap: x2, x4, x6, dan seterusnya.
Ganjil: x1, x3, x5, dan seterusnya,

3. Bilangan kompleks
 Bilangan kompleks terdiri dari bilangan Real dan Imajiner,
dimana bilangan real ada tipe rasional dan irasional.
 Bentuk bilangan kompleks seperti: Polar, Rectangular,
Trigonometri, Eksponensial, dan deret euler.

4. Transformasi Fourier
 Transformasi Fourier adalah suatu model transformasi
yang memindahkan domain spasial atau domain
waktu menjadi domain frekwensi.

5. Definisi Transformasi Fourier
 Fourier mendefinisikan transformasi Fourier dari deret
Fourier bentuk kompleks (eksponensial), yaitu dengan
menganggap fungsi non periodik adalah fungsi
periodik dengan perioda tak berhingga. Kita mulai
dengan bentuk bentuk eksponensial deret Fourier :

6. Kelebihan dan Kekurangan
transformasi Fourier
Kelebihanya adalah:
 Transformasi Fourier dapat mempermudah analisis
terhadap suatu sinyal yang berada dalam suatu sistem.
Kekuranganya adalah:
 Transformasi Fourier hanya dapat menangkap
informasi apakah suatu sinyal memiliki frekuensi
tertentu atau tidak, tapi tidak dapat menangkap
dimana frekuensi itu terjadi.

7.  Transformasi Fourier 1 dimensi ada 2, yaitu:
 Transformasi kontinu 1 dimensi
 Transformasi Diskrit 1 dimensi

8. Transformasi fourier kotinyu
 Transformasi fourier kotinyu adalah Sebuah sinyal
waktu sebagai hasil penjumlahan beberapa sinyal
kontinyu.

9. Transformasi Fourier 1-D
 Transformasi Fourier kontinu 1D dari suatu fungsi
waktu f(t) didefinisikan dengan:
 dimana F(w) adalah fungsi dalam domain frekwensi
 w adalah frekwensi atau dapat
dituliskan bahwa

10. Transformasi Fourier Diskrit
 Transformasi fourier diskrit atau disebut dengan Discrete
Fourier Transform (DFT) adalah model transformasi
fourier yang dikenakan pada fungsi diskrit, dan hasilnya
juga diskrit. DFT didefinisikan dengan :
F 𝑢 = 𝑥=1
𝑀
𝑓 𝑥 . 𝑒−𝑗𝜋𝑢𝑥/𝑀
 DFT seperti rumus di atas dinamakan dengan DFT 1
dimensi, DFT semacam ini banyak digunakan dalam
pengolahan sinyal digital.

11. Transformasi Fourier 1-D
 Transformasi Fourier dari suatu fungsi diskrit (DFT) merupakan satu
variabel, f(x), x=0,1,2, … , M-1, dirumuskan sebagai berikut :
 Dari F(u), kita akan mendapatkan kembali fungsi asal dengan
menggunakan kebalikan dari transformasi Fourier diskrit (IDFT) :
1,...,1,0)(
1
)(
1
0
/2
 



Muforexf
M
uF
M
x
Muxj 




1
0
/2
1,...,1,0)()(
M
u
Muxj
MxforeuFxf 

12. Transformasi Fourier 1-D
 |F(u)| = [R2(u) + I2(u)]1/2 disebut magnitude atau
spektrum dari transformasi Fourier dan :
disebut sudut fase atau spektrum fase dari
transformasi.






 
)(
)(
tan)( 1
uR
uI
u

13. Transformasi Fourier 1-D

15. Sifat – Sifat Transformasi

16. Sifat – Sifat Transformasi

17. Kesimpulan
 Bilangan kompleks sangat banyak digunakan,
terutama dalam berbagai sinyal. Sinyal –sinyal
tersebut telah menjadi bagian penting dalam
kehidupan kita, seperti listrik, gambar digital, suara
audio, dan sinyal –sinyal lain. Hadirnya bilangan
kompleks sangat mendukung perkembangan sinyal
sehingga teknologi dapat semakin maju seperti saat
ini. Penggunaan bilangan kompleks dan pemrosesan
sinyal dengan sistem transformasi tentu akan terus
berkembang dan menghasilkan teknologi –teknologi
baru yang lebih baik dari sebelumnya.

18. Sekian dan Terima Kasih
telah memberi semangat