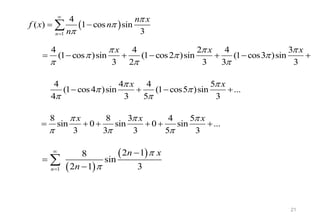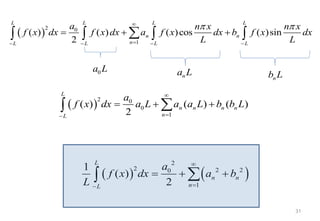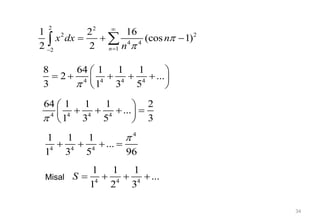Deret Fourier digunakan untuk menguraikan fungsi periodik menjadi jumlahan fungsi sinus dan kosinus dengan frekuensi yang berbeda. Koefisien Fourier ditentukan dari integral fungsi asli pada periode. Fungsi genap simetris terhadap sumbu Y dan fungsi ganjil simetris terhadap titik tengah.

1. DERET FOURIER
1

2. PERSAMAAN DIFFERENSIAL PARSIAL
Persamaan Perambatan
Gelombang
Persamaan Perambatan
Panas Satu Dimensi
METODA PENYELESAIAN
Metoda Pemisah Peubah
• Deret Fourier
• PDB, MNB

3. 1. Fungsi-fungsi Periodik
2. Definisi Deret Fourier dan Koefisien Fourier
3. Deret Fourier dengan periode sembarang
4. Deret Fourier Sinus dan Cosinus
5. Deret Fourier Sinus dan Cosinus Setengah Jangkauan
6. Identitas Parseval
Materi :
3

4. 1. Fungsi Periodik
• Fungsi f(x) disebut fungsi periodik bila
• p terkecil disebut periode dari f
( ) ( ), f
p f x p f x x D

      
Sifat fungsi periodik :
Jumlah fungsi periodik adalah periodik.
Misal 1 2
( ), ( ),..., ( )
n
f x f x f x fungsi periodik dengan periode
1 2
, ,..., ,
n
p p p maka 1 2
( ) ( ) ( ) ... ( )
n
f x f x f x f x
   
periodik dengan periode p= KPK dari 1 2
, ,..., .
n
p p p
4

5. • Fungsi y = sin x  p = 2
• Fungsi y = sin 2x  p = 
• Fungsi y = sin (nx)  p = 2/n
• Fungsi y = cos (nx)  p = 2/n
• Fungsi y = tan (x)  p = 
• Fungsi y = tan (nx)  p = /n
5

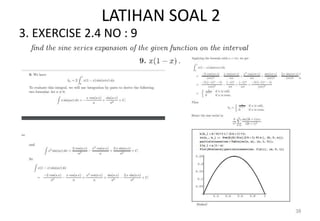
6. Fungsi f(x) dipandang periodik dengan periode
p = 4. Kita dapat menggambarkan f(x) pada interval
[ -6,6] sebagai berikut:
; 2 0
( )
;0 2
x x
f x
x x
   

 
 

2
-2 4 6
-4
-6
6

7. • Misalkan fungsi f(x) terdefinisi pada (-L,L) dan diluar interval ini,
dan f(x) periodik dengan periode 2L, kontinu bagian demi bagian,
maka Deret Fourier dari f(x) didefinisikan sebagai:
0
1
( ) cos sin
2
n n
n
a nx n x
f x a b
L L
 


 
  
 
 

1
( ) cos ,
L
n
L
n x
a f x dx
L L


 
1
( ) sin
L
n
L
n x
b f x dx
L L


 
2. Definisi Deret Fourier dan Koefisien Fourier
dengan koefisien Fourier 0, ,
n n
a a b adalah
0
1
( ) ,
L
L
a f x dx
L 
 
7

8. • Jika fungsi f(x) terdefinisi pada (0,2L) dan diluar interval ini, dan
f(x) periodik dengan periode 2L, kontinu bagian demi bagian, maka
koefisien Fourier ditentukan dengan:
2
0
1
( ) cos ,
L
n
n x
a f x dx
L L

 
2
0
1
( ) sin
L
n
n x
b f x dx
L L

 
2
0
0
1
( ) ,
L
a f x dx
L
 
8

9. 0 ; 5 0
( )
3 ; 0 5
x
f x
x
  

 
 

Tentukan Deret Fourier untuk f(x) !
Contoh :
dengan periode = 10.
Jawab :
Periode 10  L = 5
9

10. 5
0
1
3 3.
5
dx
 

5
3 5
sin
0
5 5
n x
n


 
  
 
0

5
0
5
1
( )
5
a f x dx

 
0 5
5 0
1 1
0 3cos
5 5 5
n x
dx dx


 
 
5
5
1
( )cos
5 5
n
n x
a f x dx


 
5
5
1
( )sin
5 5
n
n x
b f x dx


 
5
3 5
cos
0
5 5
n x
n


 
 
 
 
5
0
3
cos
5 5
n x
dx

 
0 5
5 0
1 1
0 3sin
5 5 5
n x
dx dx


 
 
5
0
3
sin
5 5
n x
dx

 
3(1 )
cosn
n




10

11. Maka Deret Fourier dari f(x) dituliskan berikut :
0
1
( ) cos sin
2
n n
n
a n x n x
f x a b
L L
 


 
  
 
 

1
3 3(1 cos )
sin
2 5
n
n n x
n
 




  
3 6 1 3 1 5
sin sin sin ...
2 5 3 5 5 5
x x x
  

 
    
 
 
1
3 6 1 (2 1)
sin
2 (2 1) 5
n
n x
n





 


11

12. Fungsi Genap dan Fungsi Ganjil
• Fungsi disebut fungsi genap bila berlaku
• Fungsi disebut fungsi ganjil bila berlaku
( )
f x ( ) ( ) , f
f x f x x D
   
( )
f x ( ) ( ) , f
f x f x x D
    
12
f(x) fungsi genap 
0
( ) 2 ( )
a a
a
f x dx f x dx


 
Contoh fungsi genap :
2 6 2
; 2 4 5 ; cos
y x y x x y x
    
2 2 2
( ) ( ) ( ) ( )
f x x f x x x f x
      
maka 2
( )
f x x
 fungsi genap

13. f(x) fungsi ganjil  ( ) 0
a
a
f x dx



Contoh fungsi ganjil:
3 5 3
; 3 2 ; sin
y x y x x x y x
    
13
3 3 3
( ) ( ) ( ) ( )
f x x f x x x f x
        
maka 3
( )
f x x
 fungsi ganjil

14. Sifat fungsi genap / ganjil:
• Grafik fungsi genap, simetris terhadap sumbu Y
• Grafik fungsi ganjil, simetris terhadap titik pusat.
• Hasilkali dua fungsi genap  fungsi genap
• Hasilkali dua fungsi ganjil  fungsi genap
• Hasilkali fungsi genap dan fungsi ganjil  fungsi ganjil.
( )
y f x

( )
y f x

14

15. 15
Y
a
-a
Y
a
-a
Contoh grafik fungsi genap Contoh grafik fungsi ganjil
* Hasilkali fungsi ganjil dan fungsi genap adalah fungsi ganjil.
Bukti:
Misal ( ) ( ) ( ), ( )ganjil, ( )genap
f x h x g x h x g x

maka ( ) ( ) ( )
f x h x g x
    ( ) ( ) ( )
f x h x g x
   
 f fungsi ganjil

16. Soal Latihan
Selidiki apakah fungsi berikut genap, ganjil atau tidak
keduanya
cos ;0
4. ( ) ; ( 2 ) ( )
0 ; 2
x x
f x f x f x
x


 
 

  

 

1. ( ) (1 ), 0 1 , 1
f x x x x p
    
3;0 2
2. ( ) , 4
3 ;2 4
x
f x p
x
  

 

 

3. ( ) (4 ) ; 4
f x x x p
  
16

17. • Jika f(x) fungsi ganjil terdefinisi pada ( -L,L )
• kontinu bagian demi bagian dan
• periodik dengan periode p = 2L
0
1
( ) 0,
L
L
a f x dx
L 
 

1
( ) cos 0
L
n
L
n x
a f x dx
L L


 

1
( ) sin
n
n
n x
f x b
L



 
Maka koefisien Fourier,
Sehingga Deret Fourier menjadi
Deret Fourier
Sinus
3. Deret Fourier Sinus dan Cosinus
17
0
2
( ) sin
L
n
n x
b f x dx
L L

 

18. • Jika f(x) fungsi genap terdefinisi pada ( -L,L )
• kontinu bagian demi bagian dan
• periodik dengan periode p = 2L
0
1
( ) cos
2
n
n
a n x
f x a
L



   Deret Fourier
Cosinus
Sehingga Deret Fourier menjadi
Maka koefisien Fourier,
1
( ) sin 0,
L
n
L
n x
b f x dx
L L


 

18
0
2
( ) cos
L
n
n x
a f x dx
L L

 
0
0
2
( )
L
a f x dx
L
 

19. Contoh: Tentukan Deret Fourier untuk
2 ;0 3
(1). ( )
2 ; 3 0
x
f x
x
 

 
   

-3
3
2
-2
f(x) fungsi ganjil
3
3
1
( ) sin
3 3
n
n x
b f x dx


 
, ( 6) ( )
f x f x
 
Koefisien Fourier :
Jawab:
19

20. 3
3
1
( ) sin
3 3
n
n x
b f x dx


 
0 3
3 0
1 1
2sin 2sin
3 3 3 3
n x n x
dx dx
 

  
 
0 3
2 2
cos cos
3 0
3 3
n x n x
n n
 
 

 

   
2 2
1 cos cos 1
n n
n n
 
 

     
4
1 cosn
n


 
 
1
4
( ) 1 cos sin
3
n
n x
f x n
n





 

Sehingga Deret Fouriernya :
20

21.  
1
4
( ) 1 cos sin
3
n
n x
f x n
n





 

 
 
1
2 1
8
sin
2 1 3
n
n x
n








4 4 2 4 3
(1 cos )sin (1 cos2 )sin (1 cos3 )sin
3 2 3 3 3
x x x
  
  
  
      
4 4 4 5
(1 cos4 )sin (1 cos5 )sin ...
4 3 5 3
x x
 
 
 
   
8 8 3 4 5
sin 0 sin 0 sin ...
3 3 3 5 3
x x x
  
  
     
21

22. 4. Deret Fourier Sinus & Cosinus Setengah Jangkauan
Deret Sinus atau Cosinus setengah jangkauan adalah suatu deret yang hanya
mempunyai suku-suku yang memuat sinus atau cosinus saja.
(i) Jika f(x) terdefinisi pada interval (0,L), (yaitu setengah dari interval (-L,L)
dan f(x) fungsi ganjil, maka diperoleh Deret Sinus setengah Jangkauan:
0
2
( ) sin
L
n
n x
b f x dx
L L

 
1
( ) sin
n
n
n
f x b x
L



  
0 0 ; 0 ;
n
a a
 
22

23. 0
0
2
( ) ,
L
a f x dx
L
 
0
2
( )cos , 0
L
n n
n x
a f x dx b
L L

 

0
1
( ) cos
2
n
n
a n
f x a x
L



   
(ii) Jika f(x) terdefinisi pada interval (0,L), (yaitu setengah dari interval (-L,L)
dan f(x) fungsi genap, maka diperoleh Deret Cosinus setengah Jangkauan:
23

24. 24
Bukti :
Jika f(x) fungsi genap:
1
( )cos
L
n
L
n x
a f x dx
L L


 
0
0
1 1
( )cos ( )cos
L
L
n x n x
f x dx f x dx
L L L L
 

 
 
misal ;
x u dx du
    
0 0
1 1 ( )
( )cos ( )cos ( )
L L
n x n u
f x dx f u du
L L L L
 


  
 
0
1 ( )
( )cos ( )
L
n u
f u du
L L

 
Sifat fungsi
genap
0
0
1 2
( ) ( )
L L
L
a f x dx f x dx
L L

 
 

25. 25
Sehingga
0 0
1 1
( )cos ( )cos
L L
n
n u n x
a f u du f x dx
L L L L
 
 
 
0
2
( )cos
L
n
n x
a f x dx
L L

 
1
( )sin
L
n
L
n x
b f x dx
L L


 
0
0
1 1
( )sin ( )sin
L
L
n x n x
f x dx f x dx
L L L L
 

 
 
misal ;
x u dx du
    
0 0
1 1 ( )
( )sin ( )sin ( )
L L
n x n u
f x dx f u du
L L L L
 


  
 

26. 26
0 0
1 1 ( )
( )sin ( )sin ( )
L L
n x n u
f x dx f u du
L L L L
 


  
 
0
1 ( )
( )sin ( )
L
n u
f u du
L L

  
0
1
( )sin
L
n x
f x dx
L L

  
Sehingga
0 0
1 1
( )sin ( )sin
L L
n
n x n x
b f x dx f x dx
L L L L
 
  
 
0
n
b 

27. 27
5. Identitas Parseval
jika dan
n n
a b koefisien Fourier dari ( )
f x
uniform ke pada (-L,L).
   
2
2 2 2
0
1
1
( )
2
L
n n
n
L
a
f x dx a b
L



  


Identitas Parseval menyatakan bahwa,
yang konvergen
( )
f x

28. 28
Konvergen Uniform
Andaikan terdapat sebuah deret tak hingga
1
( )
n
n
u x


 dan
1
( ) ( )
R
R n
n
S x u x

  jumlah parsial ke R dari deret tersebut.
Deret dikatakan konvergen ke ( )
f x pada suatu interval I, jika
0, N

  
Jika N hanya tergantung pada  tidak tergantung pada x, maka
( ) - ( ) untuk
R
S x f x R N

 
positif pada setiap x I
 sehingga
( ).
f x
deret dikatakan konvergen uniform ke

29. 29
Sifat deret yang konvergen uniform :
Jika masing-masing suku dari deret tak hingga kontinu pada (a,b),
dan deret konvergen uniform ke ( ),
f x maka
1. ( )
f x kontinu pada interval tersebut.
2. Deret tersebut dapat diintegralkan suku demi suku, yaitu
1 1
( ) ( )
b b
n n
n n
a a
u x dx u x dx
 
 
 

 
 
 
 

30. 30
Bukti identitas Parseval:
0
1
( )
L
L
a f x dx
L 
 
1
( )cos
L
n
L
n x
a f x dx
L L


 
1
( )sin
L
n
L
n x
b f x dx
L L


 
0
1
( ) cos sin
2
n n
n
a n x n x
f x a b
L L
 


 
  
 
 

 
2 0
1
( ) ( ) ( )cos ( )sin
2
n n
n
a n x n x
f x f x a f x b f x
L L
 


 
  
 
 

0 ( )
L
L
a L f x dx

  
( )cos
L
n
L
n x
a L f x dx
L


  
( )sin
L
n
L
n x
b L f x dx
L


  

31. 31
 
2 0
1
( ) ( ) ( )cos ( )sin
2
L L L L
n n
n
L L L L
a n x n x
f x dx f x dx a f x dx b f x dx
L L
 


   
  

   
 
2 0
0
1
( ) ( ) ( )
2
L
n n n n
n
L
a
f x dx a L a a L b b L



  


   
2
2 2 2
0
1
1
( )
2
L
n n
n
L
a
f x dx a b
L



  


n
a L
n
b L
0
a L

32. 32
Contoh:
( ) ;0 2
f x x x
   periodik dengan p=4,
(ii) tentukan 4 4 4 4
1 1 1 1
... ...
1 2 3 n
    
Jawab:
(i) ekspansikan f(x) ke dalam deret cosinus setengah jangkauan
2
0
0
2 , 0
n
a x dx b
  

2
0
2
cos
2 2
n
n x
a x dx

  2 2
2
2 4
sin cos
0
2 2
n x n x
x
n n
 
 
  
   
 
 
   
   
 
2 2
4
(cos 1), 0
n n
n


  
(i)

33. 33
0 2 2
4
2, 2, (cos 1), 0, 0.
n n
L a a n n b
n


     
0
1
( ) cos sin
2 2 2
n n
n
a n x n x
f x a b
 


  

2 2
1
4
( ) 1 (cos 1)cos
2
n
n x
f x n
n





  

2 2 2
8 1 3 1 5
1 cos cos cos ...
2 2 2
3 5
x x x
  

 
    
 
 
2 2
1
8 1 (2 1)
1 cos
2
(2 1)
n
n x
n





 


(ii)
Identitas Parseval:
   
2
2 2 2
0
1
1
( )
2
L
n n
n
L
a
f x dx a b
L



  



34. 34
2 2
2 2
4 4
1
2
1 2 16
(cos 1)
2 2 n
x dx n
n





  


4 4 4 4
8 64 1 1 1
2 ...
3 1 3 5

 
    
 
 
4 4 4 4
64 1 1 1 2
...
3
1 3 5

 
   
 
 
4
4 4 4
1 1 1
...
96
1 3 5

   
4 4 4
1 1 1
...
1 2 3
S    
Misal

35. 35
4 4 4
1 1 1
...
1 2 3
S    
4 4 4 4 4 4
1 1 1 1 1 1
... ...
1 3 5 2 4 6
   
       
   
   
4 4 4 4 4 4 4
1 1 1 1 1 1 1
... ...
1 3 5 2 1 2 3
   
       
   
   
4 4 4
1 1 1
...
16
1 3 5
S
S
 
    
 
 
4 4 4
1 1 1 15
...
16
1 3 5
S
   
4 4
15
96 16 90
S
S
 
  

36. LATIHAN SOAL 1
1. EXERCISE 2.2 NO : 9
36

37. kalkulus 1 37
2. EXERCISE 2.3 NO: 1

38. LATIHAN SOAL 2
3. EXERCISE 2.4 NO : 9
38

39. kalkulus 1 39
4. EXERCISE 2.5 NO: 7

40. Referensi
• Nakhle H. Asmar, Partial Differential Equations
with Fourier Series and Boundary Value Problems,
kalkulus 1 40