1. The document discusses Fourier transforms of discrete signals and sampling theory. It explains that continuous signals are digitized through sampling and the discrete time Fourier transform (DTFT) can be used to find the frequency spectrum of discrete signals. 2. It also covers the discrete Fourier transform (DFT) which is used when only a finite amount of data is available. The DFT breaks up a signal into its constituent frequencies. 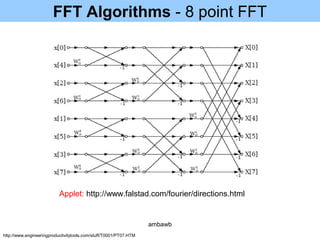3. Fast Fourier transform (FFT) algorithms like the radix-2 algorithm improve the efficiency of computing the DFT and allow it to be done in O(NlogN) time rather than O(N2) time.

1. Fourier Transforms of Discrete
Signals
Microlink IT College
ambawb

2. Sampling
• Continuous signals are digitized using digital computers
• When we sample, we calculate the value of the continuous
signal at discrete points
– How fast do we sample
– What is the value of each point
• Quantization determines the value of each samples value
ambawb

3. Sampling Periodic Functions
- Note that wb = Bandwidth, thus if then aliasing occurs
(signal overlaps)
-To avoid aliasing
-According sampling theory: To hear music up to 20KHz a CD
should sample at the rate of 44.1 KHz
ambawb

4. Discrete Time Fourier Transform
• In likely we only have access to finite amount of data
sequences (after sampling)
• Recall for continuous time Fourier transform, when the
signal is sampled:
• Assuming
• Discrete-Time Fourier Transform (DTFT):
ambawb

5. Discrete Time Fourier Transform
• Discrete-Time Fourier Transform (DTFT):
• A few points
– DTFT is periodic in frequency with period of 2π
– X[n] is a discrete signal
– DTFT allows us to find the spectrum of the discrete signal as viewed
from a window
ambawb

6. Example D
See map!
ambawb

7. Example of Convolution
• Convolution
– We can write x[n] (a periodic function) as an infinite sum of the
function xo[n] (a non-periodic function) shifted N units at a time
– This will result
– Thus
See map!
ambawb

8. Finding DTFT For periodic signals
• Starting with xo[n]
• DTFT of xo[n]
Example
ambawb

9. Example A & B
notes
notes
X[n]=a|n|
, 0 < a < 1.
ambawb

10. DT Fourier Transforms
1. Ω is in radian and it is between
0 and 2π in each discrete time
interval
2. This is different from ω where it
was between – INF and + INF
3. Note that X(Ω) is periodic
ambawb

11. Properties of DTFT
• Remember:
• For time scaling note that
m>1  Signal spreading
ambawb

12. Fourier Transform of Periodic Sequences
• Check the map~~~~~
See map!
ambawb

13. Discrete Fourier Transform
• We often do not have an infinite amount of data which is
required by DTFT
– For example in a computer we cannot calculate uncountable infinite
(continuum) of frequencies as required by DTFT
• Thus, we use DTF to look at finite segment of data
– We only observe the data through a window
– In this case the xo[n] is just a sampled data between n=0, n=N-1 (N
points)
ambawb

14. Discrete Fourier Transform
• It turns out that DFT can be defined as
• Note that in this case the points are spaced 2pi/N; thus the
resolution of the samples of the frequency spectrum is
2pi/N.
• We can think of DFT as one period of discrete Fourier series
ambawb

15. A short hand notation
remember:
ambawb

16. Inverse of DFT
• We can obtain the inverse of DFT
• Note that
ambawb

17. Using MATLAB to Calculate DFT
• Example:
– Assume N=4
– x[n]=[1,2,3,4]
– n=0,…,3
– Find X[k]; k=0,…,3
or
ambawb

18. Example of DFT
• Find X[k]
– We know k=1,.., 7; N=8
ambawb

19. Example of DFT
ambawb

20. Example of DFT
Time shift Property of DFT
Polar plot for
ambawb

21. Example of DFT
ambawb

22. Example of DFT
Summation for X[k]
Using the shift property!
ambawb

23. Example of IDFT
Remember:
ambawb

24. Example of IDFT
Remember:
ambawb

25. Fast Fourier Transform Algorithms
• Consider DTFT
• Basic idea is to split the sum into 2 subsequences of length
N/2 and continue all the way down until you have N/2
subsequences of length 2
Log2(8)
N
ambawb

26. Radix-2 FFT Algorithms - Two point FFT
• We assume N=2^m
– This is called Radix-2 FFT Algorithms
• Let’s take a simple example where only two points are given n=0, n=1; N=2
y0
y1
y0
Butterfly FFT
Advantage: Less
computationally
intensive: N/2.log(N)
Advantage: Less
computationally
intensive: N/2.log(N)
ambawb

27. General FFT Algorithm
• First break x[n] into even and odd
• Let n=2m for even and n=2m+1 for odd
• Even and odd parts are both DFT of a N/2 point
sequence
• Break up the size N/2 subsequent in half by letting
2mm
• The first subsequence here is the term x[0], x[4], …
• The second subsequent is x[2], x[6], …
1
1)2sin()2cos(
)]12[(]2[
2/
2
2/
2/
2/2/
2/
2/
2/
2
12/
0
2/
12/
0
2/
−=
=−−−==
==
=
++
−
+
−
=
−
=
∑∑
N
N
jN
N
m
N
N
N
m
N
Nm
N
mk
N
mk
N
N
m
mk
N
k
N
N
m
mk
N
W
jeW
WWWW
WW
mxWWmxW
πππ
ambawb

28. Example
1
1)2sin()2cos(
)]12[(]2[][
2/
2
2/
2/
2/2/
2/
2/
2/
2
12/
0
2/
12/
0
2/
−=
=−−−==
==
=
++=
−
+
−
=
−
=
∑∑
N
N
jN
N
m
N
N
N
m
N
Nm
N
mk
N
mk
N
N
m
mk
N
k
N
N
m
mk
N
W
jeW
WWWW
WW
mxWWmxWkX
πππ
Let’s take a simple example where only two points are given n=0, n=1; N=2
]1[]0[]1[]0[)]1[(]0[]1[
]1[]0[)]1[(]0[]0[
1
1
0
0
1.0
1
1
1
0
0
1.0
1
0
0
0.0
1
0
1
0
0
0.0
1
xxxWxxWWxWkX
xxxWWxWkX
mm
mm
−=+=+==
+=+==
∑∑
∑∑
==
==
Same result
ambawb

29. FFT Algorithms - Four point FFT
First find even and odd parts and then combine them:
The general form:
ambawb

30. FFT Algorithms - 8 point FFT
http://www.engineeringproductivitytools.com/stuff/T0001/PT07.HTM
Applet: http://www.falstad.com/fourier/directions.html
ambawb

31. A Simple Application for FFT
t = 0:0.001:0.6; % 600 points
x = sin(2*pi*50*t)+sin(2*pi*120*t);
y = x + 2*randn(size(t));
plot(1000*t(1:50),y(1:50))
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('time (milliseconds)')
Taking the 512-point fast Fourier transform (FFT): Y = fft(y,512)
The power spectrum, a measurement of the power at various
frequencies, is Pyy = Y.* conj(Y) / 512;
Graph the first 257 points (the other 255 points are redundant) on a
meaningful frequency axis: f = 1000*(0:256)/512;
plot(f,Pyy(1:257))
title('Frequency content of y')
xlabel('frequency (Hz)')
This helps us to design an effective filter!
ML Help!
ambawb

32. Example
• Express the DFT of the 9-point {x[0], …,x[9]} in terms of the
DFTs of 3-point sequences {x[0],x[3],x[6]}, {x[1],x[4],x[7]},
and {x[2],x[5],x[8]}.
ambawb

33. References
• Read Schaum’s Outlines: Chapter 6
• Do Chapter 12 problems: 19, 20, 26, 5, 7
ambawb