6 Transformasi Fourier Waktu Diskret.pdf

f(t) f[n]
F(w) F(W)
F(s) F(z)
Control Systems Engineering, Electrical Engineering Department, FTEIC-ITS
Matlab Computation Simulink Simulation
TRANSFORMASI FOURIER WAKTU DISKRET
Analisis, Komputasi, dan Simulasi
4. Sifat Trans. Fourier
5. Respons Frekuensi
1. Deret Fourier
2. Sifat Deret Fourier
3. Transformasi Fourier
6. Respons Sistem dengan
Input Periodik
7. Transf. Fourier Sinyal
Kontinu Tersampel

Pengantar
SINYAL DAN SISTEM: Analisis, Komputasi, dan Simulasi
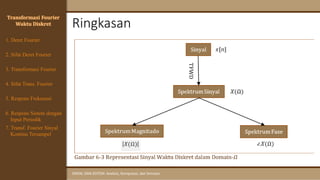
Transformasi Fourier
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

Deret Fourier Waktu Diskret
Waktu Diskret
Deret Fourier Waktu Diskret didefinisikan melalui pasangan
persamaan berikut.
Persamaan Sintesis
𝑥[𝑛] = ෍
𝑘=<𝑁>
𝑎𝑘𝑒𝑗𝑘(𝛺)𝑛
dan Persamaan Analisis
𝑎𝑘 =
1
𝑁
෍
𝑛=<𝑁>
𝑥[𝑛]𝑒−𝑗𝑘(𝛺)𝑛
Koefisien deret Fourier 𝑎𝑘 disebut juga Koefisien Spektral.
1. Deret Fourier
Input Periodik
Kontinu Tersampel

Deret Fourier Waktu Diskret
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

1. Pergeseran waktu
Waktu Diskret
Jika 𝑦[𝑛] = 𝑥[𝑛 − 𝑚],
Maka
𝑏𝑘 = 𝑎𝑘𝑒−𝑗𝑘𝛺𝑚
di mana
𝑏𝑘: koefisien deret 𝑦[𝑛]
𝑎𝑘: koefisien deret 𝑥[𝑛]
1. Deret Fourier
Input Periodik
Kontinu Tersampel

2. Linearitas
Waktu Diskret
Jika 𝑧[𝑛] = 𝛼𝑥[𝑛] + 𝛽𝑦[𝑛]
Maka
𝑐𝑘 = 𝛼𝑎𝑘 + 𝛽𝑏𝑘
di mana
𝑐𝑘: koefisien deret 𝑧[𝑛]
1. Deret Fourier
Input Periodik
Kontinu Tersampel

2. Linearitas
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

3. Konvolusi periodik
Waktu Diskret
Jika 𝑧[𝑛] = 𝑥[𝑛] ⊗ 𝑦[𝑛]
Maka
𝑐𝑘 = 𝑁𝑎𝑘𝑏𝑘
di mana
1. Deret Fourier
Input Periodik
Kontinu Tersampel

4. Konvolusi penjumlahan
Waktu Diskret
Jika 𝑦[𝑛] = 𝑥[𝑛] ∗ ℎ[𝑛]
Maka
𝑏𝑘 = 𝑎𝑘𝐻[𝑘𝛺]
di mana
1. Deret Fourier
Input Periodik
Kontinu Tersampel

5. Modulasi
Waktu Diskret
Jika 𝑧[𝑛] = 𝑥[𝑛]𝑦[𝑛]
Maka
𝑐𝑘 = 𝑎𝑘 ⊗ 𝑏𝑘
di mana
1. Deret Fourier
Input Periodik
Kontinu Tersampel

Transformasi Fourier Waktu Diskret
Waktu Diskret
Transformasi Fourier waktu diskret didefinisikan oleh
pasangan persamaan
𝑋(𝛺) = ෍
𝑛=−∞
∞
𝑥 𝑛 𝑒−𝑗𝛺𝑛
dan
𝑥 𝑛 =
1
2𝜋
න
2𝜋
𝑋(𝛺)𝑒𝑗𝛺𝑛
𝑑𝛺
atau
𝑋 𝛺 = ℱ 𝑥 𝑛 ; 𝑥 𝑛 = ℱ−1 𝑋(𝛺)
1. Deret Fourier
Input Periodik
Kontinu Tersampel

Transformasi Fourier Waktu Diskret
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

1. Periodisitas
Transformasi Fourier waktu diskret merupakan fungsi periodik
terhadap 𝛺 dengan periode 2𝜋.
𝑋 𝛺 + 2𝜋 = 𝑋(𝛺)
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

2. Linearitas
Jika
ℱ 𝑥1[𝑛] = 𝑋1(𝛺) dan ℱ 𝑥2[𝑛] = 𝑋2(𝛺)
maka
ℱ 𝛼𝑥1[𝑛] + 𝛽𝑥2[𝑛] = 𝛼𝑋1(𝛺) + 𝛽𝑋2(𝛺)
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

3. Pergeseran waktu
Jika
ℱ 𝑥[𝑛] = 𝑋(𝛺)
maka
ℱ 𝑥 𝑛 − 𝑛0 = 𝑒−𝑗𝛺𝑛0𝑋(𝛺)
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

4. Pergeseran frekuensi
Jika
ℱ 𝑥[𝑛] = 𝑋(𝛺)
maka
ℱ 𝑥 𝑛 𝑒𝑗𝛺0𝑛 = 𝑋 𝛺 − 𝛺0
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

5. Derivatif dalam domain frekuensi
Jika
ℱ 𝑥[𝑛] = 𝑋(𝛺)
maka
ℱ 𝑛𝑥 𝑛 = 𝑗
𝑑𝑋(𝛺)
𝑑𝛺
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

5. Derivatif dalam domain frekuensi
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

6. Teorema Parseval
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel
Energi sinyal waktu diskret
𝐸 = lim
𝑁→∞
෍
𝑛=−𝑁
𝑁
𝑥[𝑛] 2
= ෍
𝑛=−∞
∞
𝑥[𝑛] 2
Dalam domain-𝛺 menjadi
𝐸 = ෍
𝑛=−∞
∞
𝑥[𝑛] 2 =
1
2𝜋
න
−𝜋
𝜋
𝑋(𝛺) 2𝑑𝛺

7. Konvolusi dan modulasi
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel
Jika
𝑦 𝑛 = ℎ 𝑛 ∗ 𝑥 𝑛
maka
𝑌(𝛺) = 𝐻(𝛺)𝑋(𝛺)

7. Konvolusi dan modulasi
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel
Jika
𝑦 𝑛 = 𝑥1 𝑛 𝑥2 𝑛
maka
𝑌(𝛺) = ෍
𝑛=∞
∞
𝑥1 𝑛 𝑥2 𝑛 𝑒−𝑗𝛺𝑛 = 𝑋1(𝛺) ⊗ 𝑋2(𝛺)

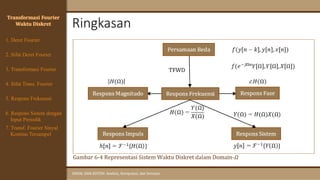
Respons Frekuensi
Respons Frekuensi atau Fungsi Transfer Sinusoidal dari sistem.
𝐻(𝛺) = ෍
𝑘=−∞
∞
ℎ[𝑘] 𝑒−𝑗𝛺𝑘
Perhatikan bahwa respons frekuensi tidak lain merupakan transformasi Fourier
dari respons impuls.
Jika 𝑋(𝛺), 𝑌(𝛺) dan 𝐻(𝛺) masing-masing merupakan transformasi Fourier dari
𝑥[𝑛], 𝑦[𝑛] dan ℎ[𝑛], maka
𝐻(𝛺) =
𝑌(𝛺)
𝑋(𝛺)
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

Respons Frekuensi
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel
Berdasar PB input-output sistem
෍
𝑘=0
𝑁
𝑎𝑘 𝑦[𝑛 − 𝑘] = ෍
𝑘=0
𝑀
𝑏𝑘𝑥[𝑛 − 𝑘]
Respons Frekuensi dapat diperoleh
𝐻(𝛺) =
𝑌(𝛺)
𝑋(𝛺)
=
σ𝑘=0
𝑀
𝑏𝑘𝑒−𝑗Ω𝑘
σ𝑘=0
𝑁
𝑎𝑘𝑒−𝑗Ω𝑘

Respons Frekuensi
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

Respons Sistem dengan Input Periodik
Jika
𝑥[𝑛] = 𝑒𝑗𝛺𝑛 → 𝑦[𝑛] = 𝑒𝑗𝛺𝑛𝐻(𝛺)
Maka
𝑥[𝑛] = ෍
𝑘=−∞
∞
𝑎𝑘 𝑒𝑗𝑘𝛺𝑛
→ 𝑦[𝑛] = ෍
𝑘=−∞
∞
𝑎𝑘 𝑒𝑗𝑘𝛺𝑛
𝐻(𝛺𝑘)
atau
𝑦 𝑛 = ෍
𝑘=−∞
∞
𝑑𝑘𝑒𝑗𝑘𝛺𝑛 ; 𝑑𝑘 = 𝑎𝑘𝐻(𝛺𝑘)
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

Respons Sistem dengan Input Periodik
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

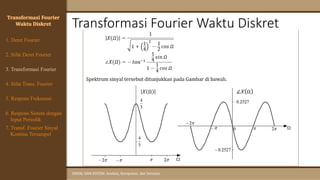
Transformasi Fourier Sinyal Tersampel
Jika sinyal kontinu 𝑥𝑎(𝑡) disampling, maka sinyal tersampel tersebut
dapat dipandang sebagai sinyal waktu diskret 𝑥[𝑛] (di mana 𝑥 𝑛 =
𝑥𝑎 𝑛𝑇 ), maka transformasi Fouriernya adalah
𝑋(𝛺) = ෍
𝑛=−∞
∞
𝑥 𝑛 𝑒−𝑗𝛺𝑛
Jika dipandang sebagai sinyal waktu kontinu 𝑥𝑠(𝑡) (di mana 𝑥𝑠 𝑡 =
𝑥𝑎(𝑡) σ𝑛=−∞
∞ 𝛿 𝑡 − 𝑛𝑇 )., maka transformasi Fouriernya
𝑋𝑠 𝜔 =
1
𝑇
෍
𝑟=−∞
∞
𝑋𝑎 𝜔 + 𝑟𝜔𝑠 atau 𝑋𝑠(𝜔) = ෍
𝑛=−∞
∞
𝑥𝑎 𝑛𝑇 𝑒−𝑗𝜔𝑛𝑇
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

Ringkasan
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

Latihan
• Kerjakan semua latihan Bab 6 Transformasi Fourier
Waktu Diskret
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

Sumber
Penulis Yusuf Bilfaqih Ali Fatoni Achmad Jazidie
Institusi Institut Teknologi Sepuluh Nopember
Kategori Buku Ajar
Bidang Ilmu Teknik
ISBN 9786230269219
Penerbit Deepublish
Ukuran 17.5×25 cm
Halaman xxxv, 376 hlm
Jenis Cover Softcover
Tahun 2023
Waktu Diskret
1. Deret Fourier
Input Periodik
Kontinu Tersampel

6 Transformasi Fourier Waktu Diskret.pdf

More Related Content

What's hot

Similar to 6 Transformasi Fourier Waktu Diskret.pdf

More from yusufbf

6 Transformasi Fourier Waktu Diskret.pdf