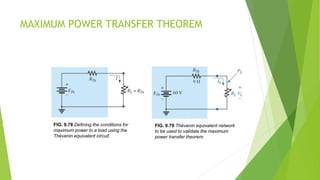
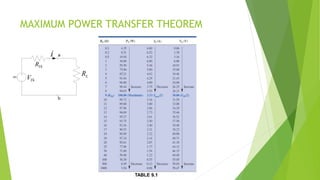
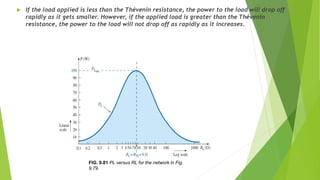
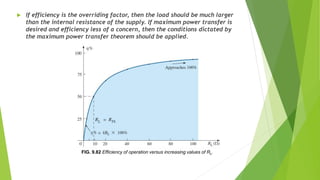
1) The maximum power transfer theorem states that maximum power is delivered to a load when its resistance equals the internal resistance of the voltage source, as represented by the Thevenin equivalent circuit. 2) When the load resistance is less than the Thevenin resistance, the power delivered to the load decreases rapidly as the load resistance decreases. 3) For maximum power transfer, the load resistance should be set equal to the Thevenin resistance according to the maximum power transfer theorem.

1. MAXIMUM POWER
TRANSFER
THEOREM
ASHWANI KUMAR
14030141EEE016

2. MAXIMUM POWER TRANSFER THEOREM
 The total power delivered by a supply such as ETh is
absorbed by both the Thévenin equivalent resistance
and the load resistance. Any power delivered by the
source that does not get to the load is lost to the
Thévenin resistance.
DC
b
a
LR
i
ThR
ThV

3. MAXIMUM POWER TRANSFER THEOREM
 When designing a circuit, it is often important to be able to answer one of the
following questions:
 What load should be applied to a system to ensure that the load is receiving
maximum power from the system?
 Conversely:
 For a particular load, what conditions should be imposed on the source to
ensure that it will deliver the maximum power available?
DC
b
a
LR
i
ThR
ThV

4. 4
DC
b
a
LR
i
ThR
ThV
The power delivered to the load (absorbed by RL) is
 
22
L Th Th L Lp i R V R R R    
This power is maximum when
   
2 32
2 0Th Th L L Th L
L
p
V R R R R R
R
       
 
0Lp R  

5. 5
   
2 32
2 0Th Th L L Th L
L
dp
V R R R R R
dR
 
     
 
2Th L LR R R 
L ThR R
 
2
max L Th
Th Th L L R R
p V R R R 
   
 
2 2
max 2 4Th Th Th Th Thp V R R V R   
Thus, maximum power transfer takes place when the resistance of the load
equals the Thevenin resistance RTh. Note also that
Thus, at best, one-half of the power is dissipated in the internal resistance and
one-half in the load.

6. MAXIMUM POWER TRANSFER THEOREM
FIG. 9.78 Defining the conditions for
maximum power to a load using the
Thévenin equivalent circuit.
FIG. 9.79 Thévenin equivalent network
to be used to validate the maximum
power transfer theorem.

7. MAXIMUM POWER TRANSFER THEOREM
TABLE 9.1
DC
b
a
LR
i
ThR
ThV

8.  If the load applied is less than the Thévenin resistance, the power to the load will drop off
rapidly as it gets smaller. However, if the applied load is greater than the Thévenin
resistance, the power to the load will not drop off as rapidly as it increases.
FIG. 9.81 PL versus RL for the network in Fig.
9.79.

9. FIG. 9.82 Efficiency of operation versus increasing values of RL.
 If efficiency is the overriding factor, then the load should be much larger
than the internal resistance of the supply. If maximum power transfer is
desired and efficiency less of a concern, then the conditions dictated by
the maximum power transfer theorem should be applied.

10. BIBLIOGRAPHY
Introductory Circuit Analysis by
Boylested
http://www.secs.oakland.edu