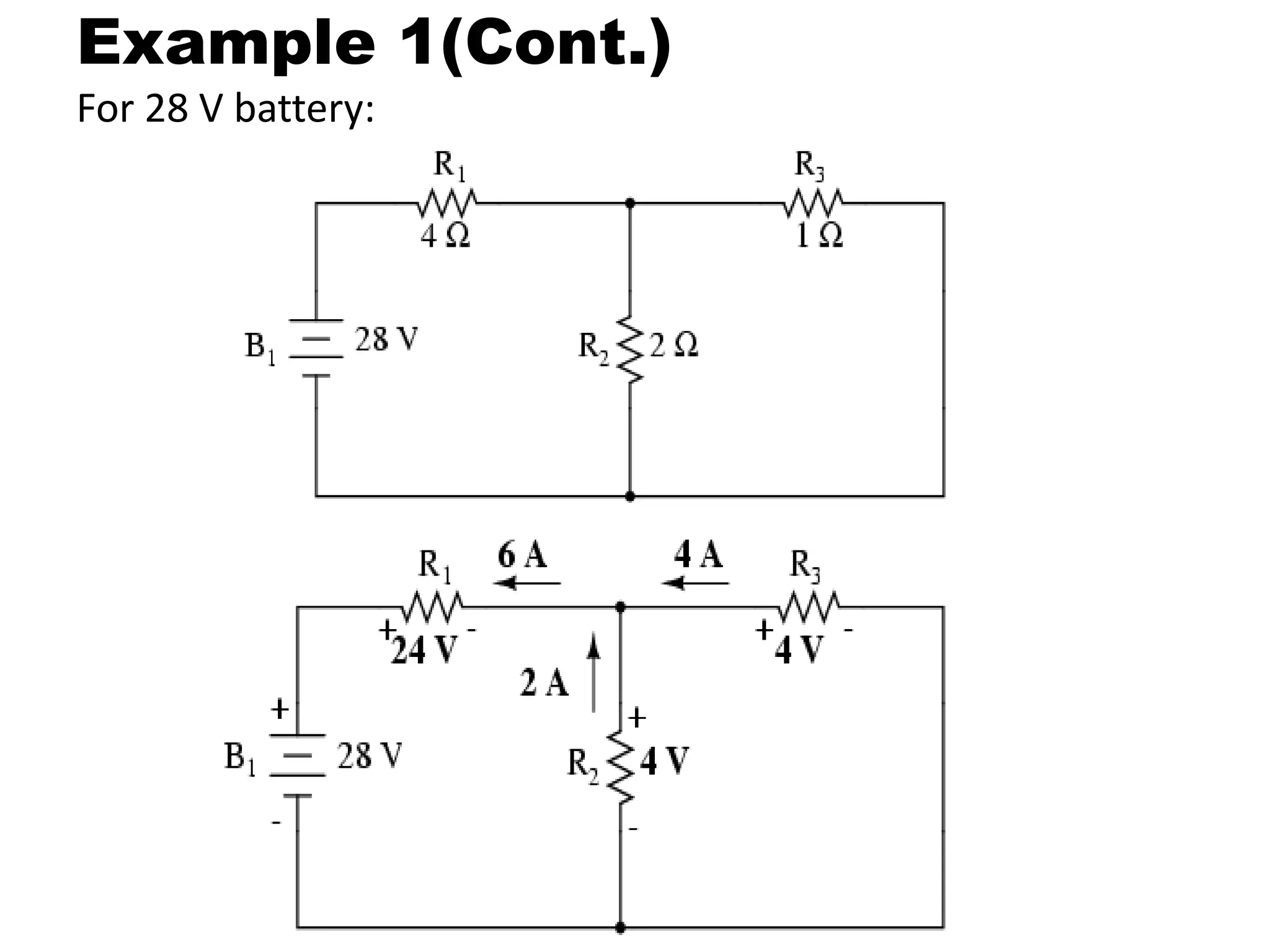
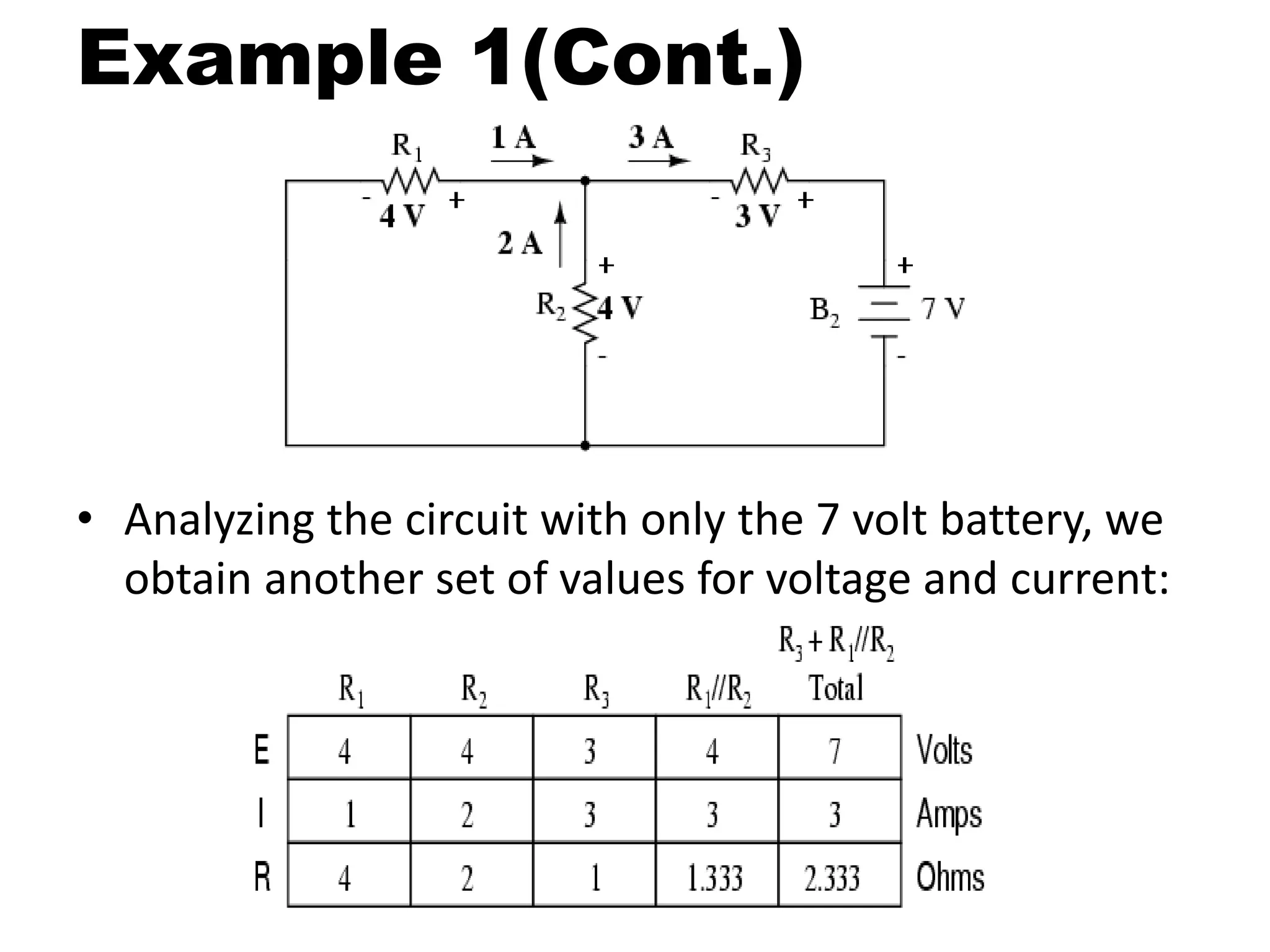
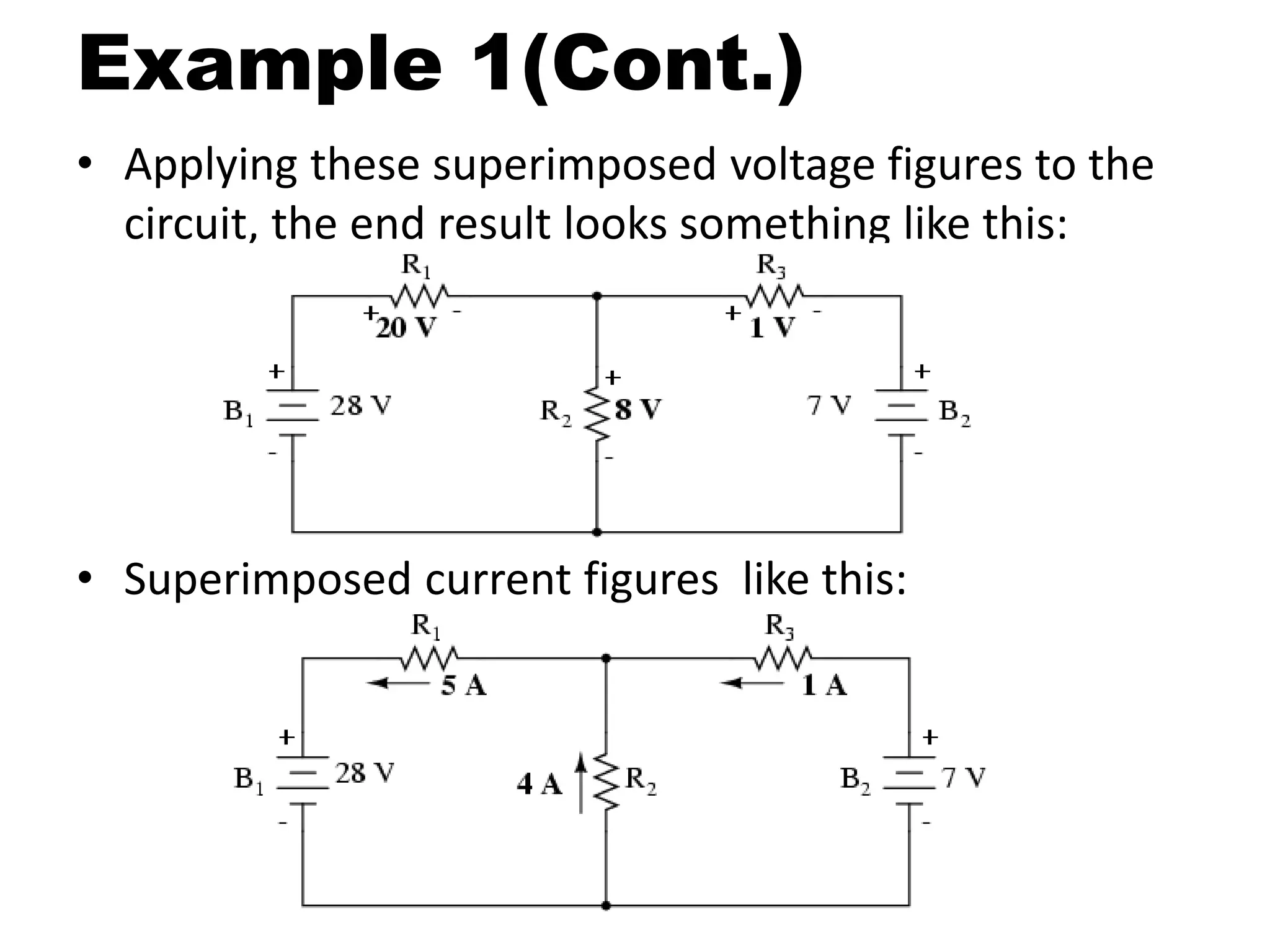
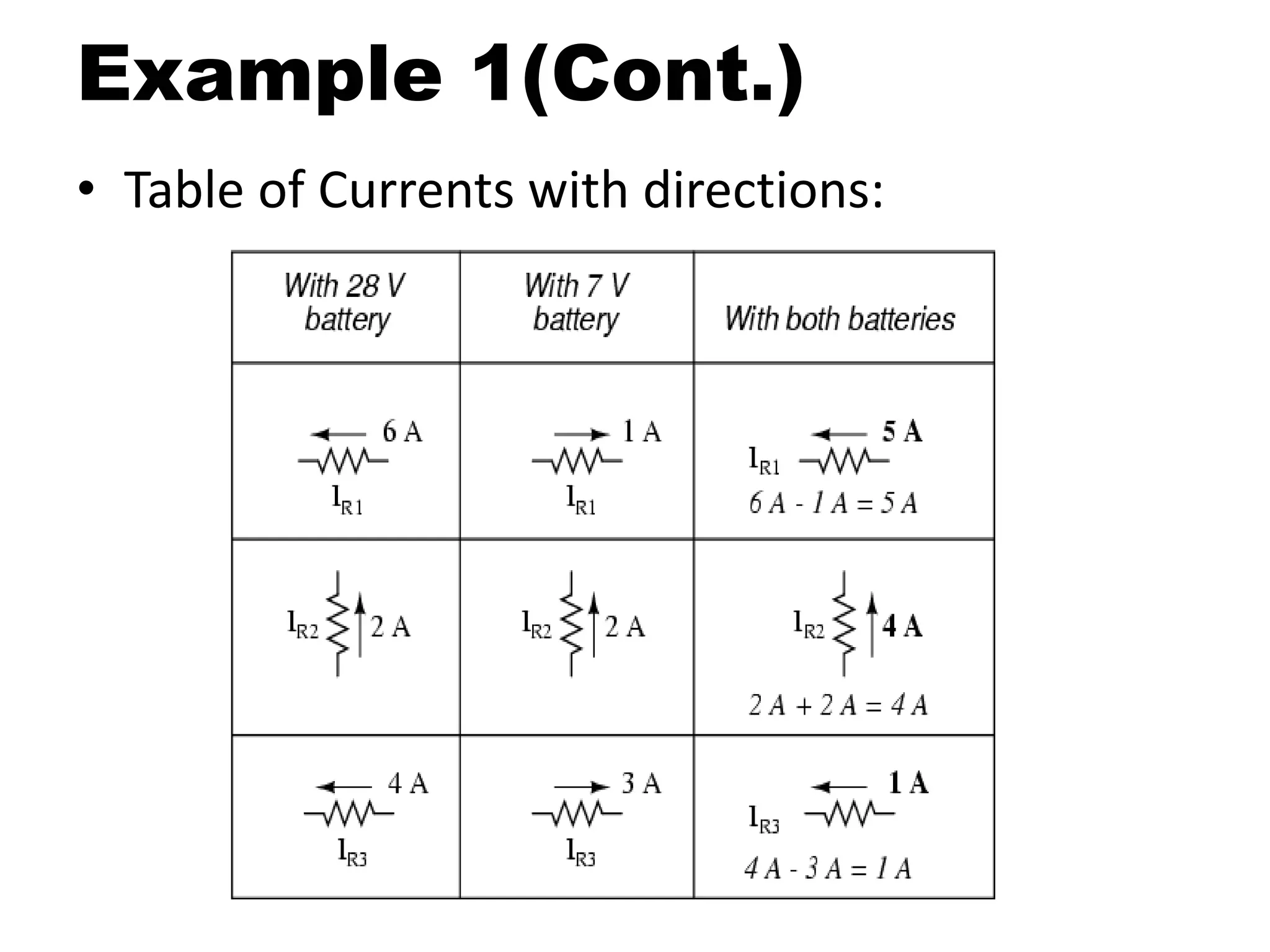
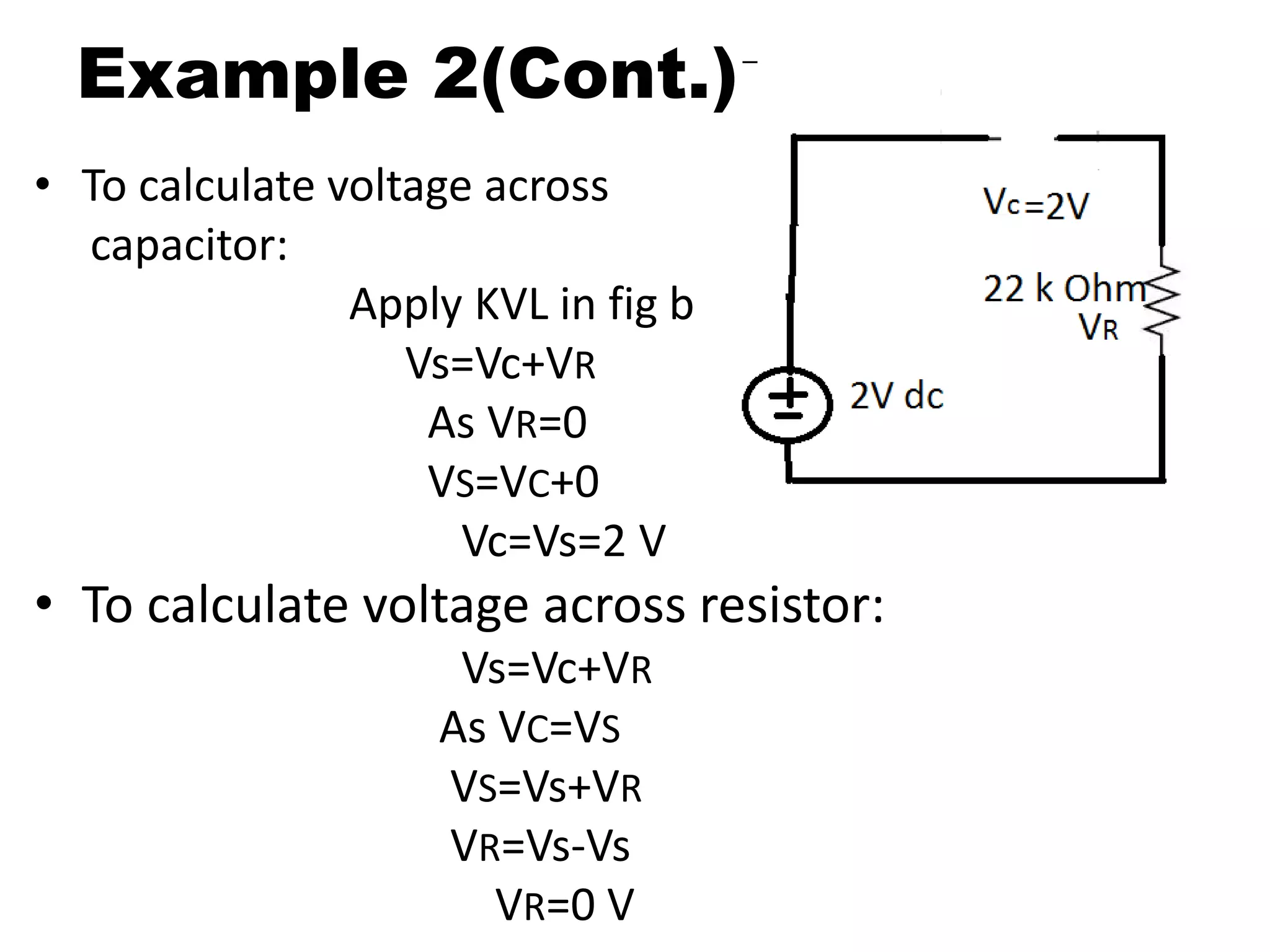
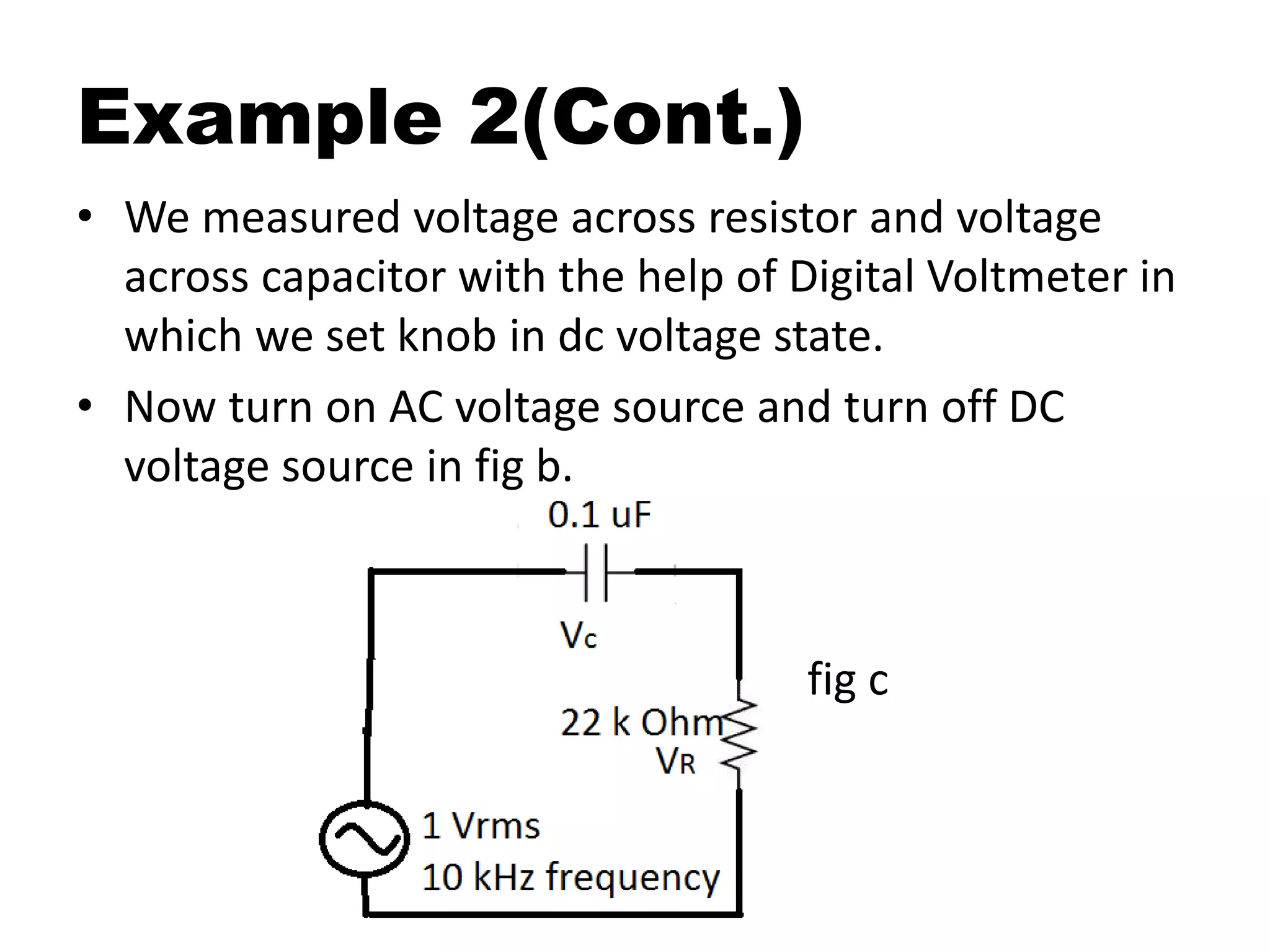
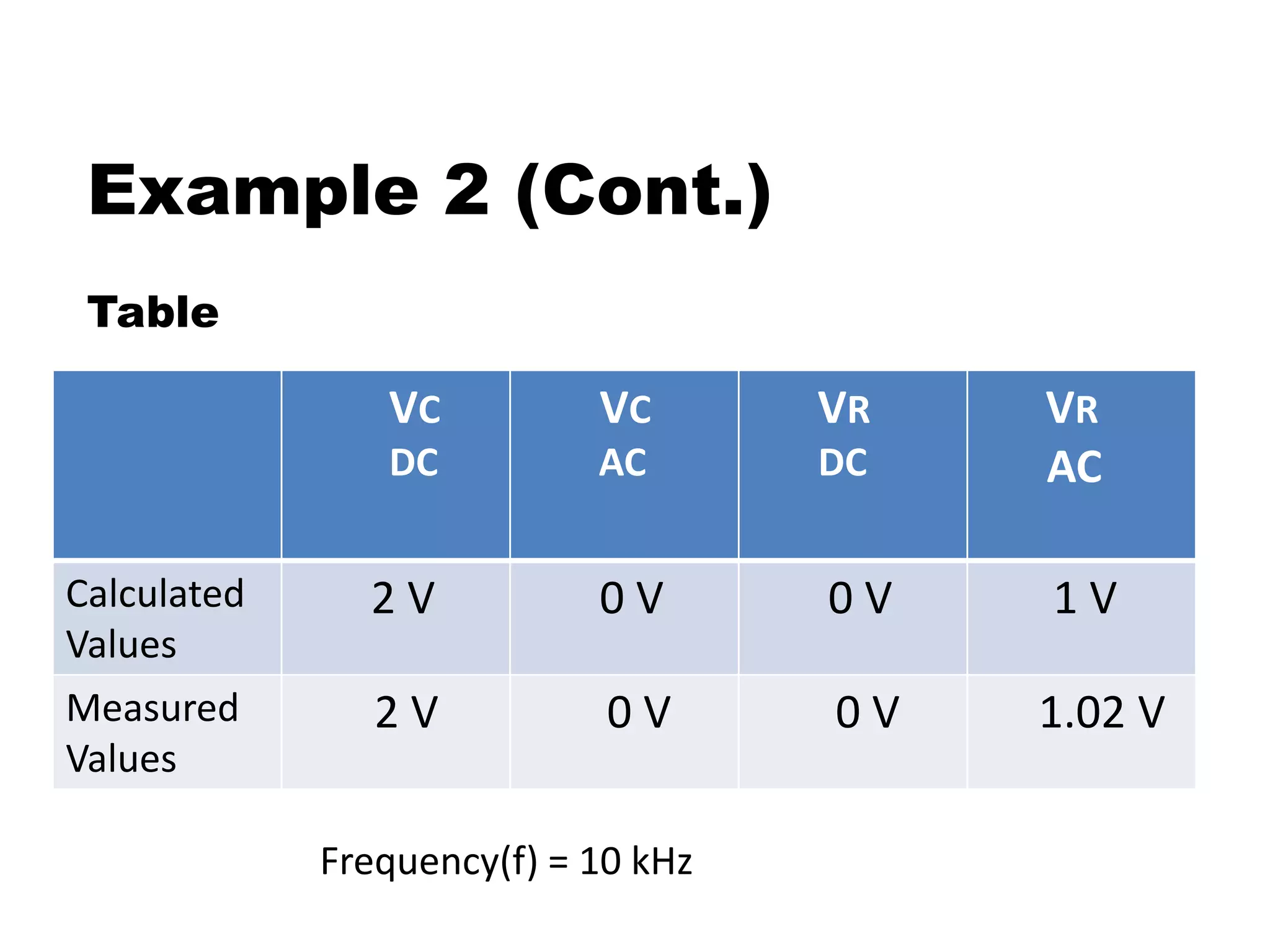
This document discusses superposition and its use in analyzing circuits with both AC and DC sources. Superposition allows a circuit to be solved by separately analyzing the individual effects of each independent source. The key steps are to solve the circuit for each source alone by shorting or opening the other sources; then combine the individual voltage and current results. Example 1 uses two DC sources in a circuit to demonstrate the technique. Example 2 applies superposition to an RC circuit with both an AC and DC source, calculating and measuring the separate and combined voltage effects across the resistor and capacitor.

1. Superposition
of
AC and DC Sources
Presented by:
M. Hammad Waseem
L1F14BSEE0033
November 30, 2015

2. Contents of Presentation
• What is Superposition?
• Usage of Superposition.
• Steps of Superposition with dc independent
sources.
• Example 1 - Using two independent DC
sources.
• Steps of superposition with ac and dc sources.
• Example 2 - Using AC and DC sources in RC
circuit.

3. What is Superposition?
• The voltage across a component is the
algebraic sum of the voltage across the
component due to each independent source
acting upon it.
• The current flowing through a component is
the algebraic sum of the current flowing
through component due to each independent
source acting upon it.

4. Usage of Superposition
• Separating the contributions of the DC and AC
independent sources.
Example:
To determine the performance of an amplifier, we
calculate the DC voltages and currents to establish
the bias point.
The AC signal is usually what will be amplified.
A generic amplifier has a constant DC operating
point, but the AC signal’s amplitude and frequency
will vary depending on the application.

5. Usage of Superposition (Cont.)
 Superposition can be used to reduce the
complexity of a circuit so that the voltages and
currents in the circuit can be determined easily.
 To turn off a voltage source, replace it with a short
circuit.
 To turn off a current source, replace it with an open
circuit.
 Polarity of voltage across components and direction of
currents through the components must be the same
during each iteration through the circuit.
 The total of the currents and voltages from each
iteration is the solution when all sources are active in
the circuit

6. Steps of Superposition with
DC Independent Sources
• Turn off all independent sources except one.
• Redraw circuit.
• Solve for the voltages and currents in the new
circuit.
• Turn off the active independent source and turn
on one of the other independent sources.
• Repeat Steps 2 and 3.
• Continue until you have turned on each of the
independent sources in the original circuit.
• To find the total voltage across each component
and the total current flowing, add the
contributions from each of the voltages and
currents found in Step 3.

7. Example 1
Using two independent DC sources:
• Since we have two sources of power in this circuit,
we will have to calculate two sets of values for
voltage drops and/or currents, one for the circuit
with only the 28 volt battery in effect and one for the
circuit with only the 7 volt battery in effect.

8. Example 1(Cont.)
For 28 V battery:

9. Example 1 (Cont.)
• Analyzing the circuit with only the 28 volt battery, we
obtain the following values for voltage and current:
• For 7 V battery:

10. Example 1(Cont.)
• Analyzing the circuit with only the 7 volt battery, we
obtain another set of values for voltage and current:

11. Example 1(Cont.)
• Applying these superimposed voltage figures to the
circuit, the end result looks something like this:
• Superimposed current figures like this:

12. Example 1(Cont.)
• Table of Voltages with polarities:

13. Example 1(Cont.)
• Table of Currents with directions:

14. Steps of Superposition with
AC and DC Sources
• Turn off AC voltage source except DC voltage source.
• Redraw the circuit.
• In RC circuit, capacitor act as an open for DC voltage
source whereas in RL circuit inductor act as closed
for DC voltage source.
• Calculate and measured DC voltages across
capitor(or inductor) and resistor.
• For DC source, if we use RC circuit then voltage
across capacitor is equal to DC supply voltage, and
voltage across resistor is zero. Else if we use RL circuit
then voltage across inductor is zero, and voltage
across resistor is equal to dc supply voltage.

15. Steps of Superposition with
AC and DC sources (Cont.)
• Now turn on AC voltage source and turn off DC voltage
source.
• Repeat step 2.
• In RC circuit, capacitor act as short for AC voltage source
whereas in RL circuit, inductor act as open for AC voltage
source.
• Calculate and measured AC voltages across capacitor(or
inductor) and resistor.
• For ac source, if we use RC circuit then voltage across
resistor is equal to AC supply voltage, and voltage across
capacitor is zero. Else if we use RL circuit then voltage
across resistor is zero, and voltage across inductor is
equal to AC supply voltage.
• Superimposed both the sources and check AC and DC
voltages across capacitor(or inductor) and resistor with
the help of oscilloscope in AC coupling and DC coupling.

16. Example 2:
Using AC and DC sources in RC circuit:
fig a fig b
• In fig b, we remove the ac voltage source.
• We calculate and measure DC voltages across
capacitors and resistors.

17. Example 2(Cont.):
• To calculate voltage across
capacitor:
Apply KVL in fig b
Vs=Vc+VR
As VR=0
VS=VC+0
Vc=Vs=2 V
• To calculate voltage across resistor:
Vs=Vc+VR
As VC=VS
VS=Vs+VR
VR=Vs-Vs
VR=0 V

18. Example 2(Cont.)
• We measured voltage across resistor and voltage
across capacitor with the help of Digital Voltmeter in
which we set knob in dc voltage state.
• Now turn on AC voltage source and turn off DC
voltage source in fig b.
fig c

19. Example 2(Cont.)
• To calculate voltage across
capacitor:
Vs=Vc+VR
As VR=VS
VS=Vc+Vs
Vc=Vs-Vs
Vc=0 V
• To calculate voltage across
resistor:
Vs=Vc+VR
As Vc=0 V
VS=0+VR
VR=Vs=1 V

20. Example 2 (Cont.)
Table
VC
DC
VC
AC
VR
DC
VR
AC
Calculated
Values
2 V 0 V 0 V 1 V
Measured
Values
2 V 0 V 0 V 1.02 V
Frequency(f) = 10 kHz

21. Thank You