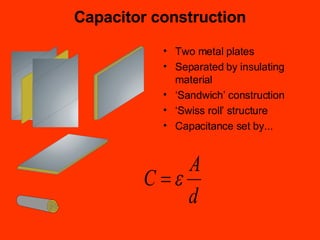
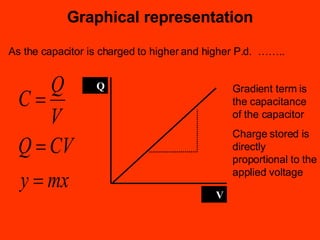
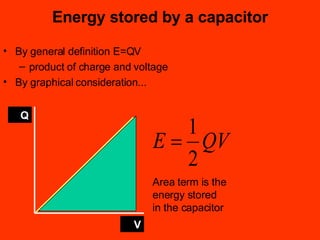
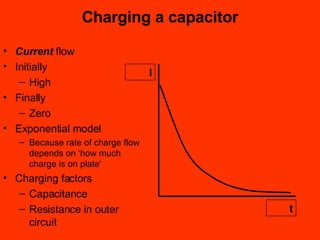
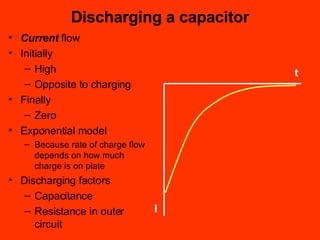
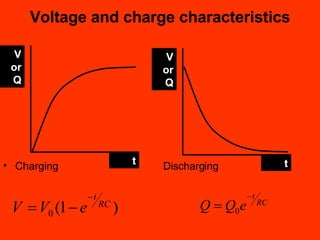
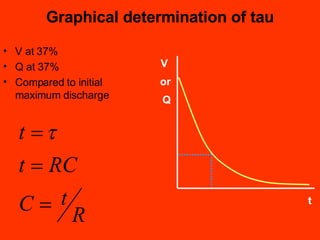
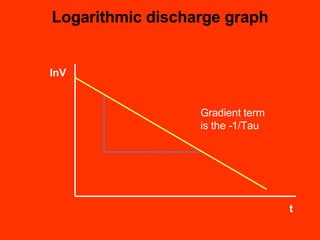
A capacitor is an electronic component that stores an electrical charge. It consists of two conducting surfaces separated by an insulating material. The amount of charge a capacitor can store is defined by its capacitance, which depends on the size and separation of the conducting plates and the material between them. When a voltage is applied across a capacitor's plates, electric current initially flows high as the capacitor charges, then tapers off to zero as it reaches full charge. This exponential charging and discharging process is characterized by the capacitor's time constant, the product of its capacitance and the resistance in the charging/discharging circuit.

1. Capacitors revision

2. What is a capacitor? Electronic component Two conducting surfaces separated by an insulating material Stores charge Uses Time delays Filters Tuned circuits

3. Capacitor construction Two metal plates Separated by insulating material ‘ Sandwich’ construction ‘ Swiss roll’ structure Capacitance set by...

4. Defining capacitance ‘ Good’ capacitors store a lot of charge… … when only a small voltage is applied Capacitance is charge stored per volt Capacitance is measured in farads F Big unit so nF, mF and  F are used

5. Graphical representation As the capacitor is charged to higher and higher P.d. …….. Gradient term is the capacitance of the capacitor Charge stored is directly proportional to the applied voltage Q V

6. Energy stored by a capacitor By general definition E=QV product of charge and voltage By graphical consideration... Area term is the energy stored in the capacitor Q V

7. Other expressions for energy By substitution of Q=CV

8. Charging a capacitor Current flow Initially High Finally Zero Exponential model Because rate of charge flow depends on ‘how much charge is on plate' Charging factors Capacitance Resistance in outer circuit I t

9. Discharging a capacitor Current flow Initially High Opposite to charging Finally Zero Exponential model Because rate of charge flow depends on how much charge is on plate Discharging factors Capacitance Resistance in outer circuit I t

10. Voltage and charge characteristics Charging Discharging V or Q t V or Q t

11. Product of Capacitance of the capacitor being charged Resistance of the charging circuit CR Symbol  ‘Tau’ Unit seconds To show units of tau are seconds, use Ohm’s Law to substitute for R and Capacitance definition to substitute for C Time constant

12. When t equals tau during discharge Discharging: At t = tau the capacitor has fallen to 37% of its original value. Charging :By a similar analysis tau can be considered to be the time taken for the capacitor to reach 63% of full charge.

13. Graphical determination of tau V at 37% Q at 37% Compared to initial maximum discharge V or Q t

14. Logarithmic discharge analysis Mathematical consideration of discharge Exponential relationship Taking natural logs produces expression of form ‘y=mx+c’ Gradient is -1/Tau

15. Logarithmic discharge graph Gradient term is the -1/Tau lnV t