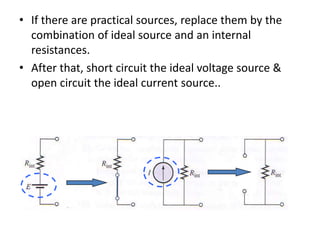
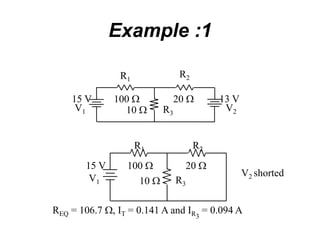
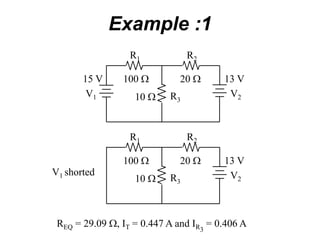
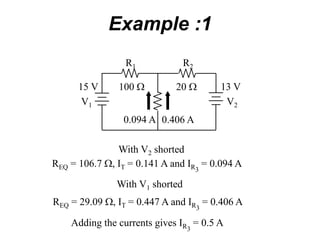
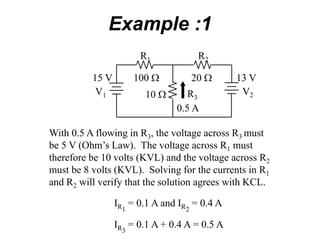
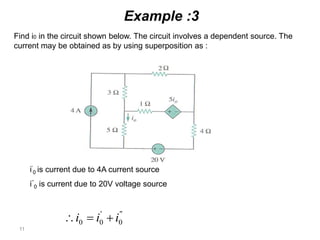
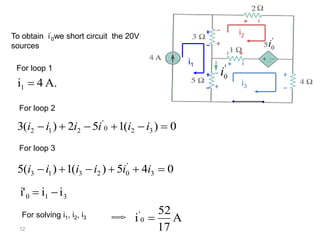
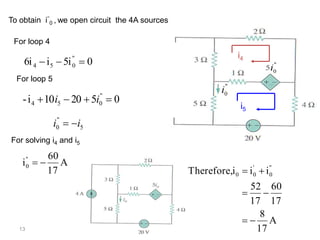
The superposition theorem allows analysts to determine the voltage across or current through an element in a linear, bilateral circuit containing multiple sources. It states that the response of such a circuit to multiple sources is equal to the sum of the responses to each source acting alone. To apply the theorem, each independent source is solved for separately while other sources are removed by shorting or opening. Dependent sources are left intact. The procedure is demonstrated through examples solving for currents using superposition in circuits with independent and dependent sources.

1. Superposition Theorem
• The superposition theorem extends the use of Ohm’s
Law to circuits with multiple sources.
• Statement:- “The current through, or voltage across,
an element in a linear bilateral network equal to the
algebraic sum of the currents or voltages produced
independently by each source.”
• Superposition theorem is very helpful in determining
the voltage across an element or current through a
branch when the circuit contains multiple number of
voltage or current sources.

2.  In order to apply the superposition theorem to a network,
certain conditions must be met :
• All the components must be linear, for e.g.- the current is
proportional to the applied voltage (for resistors), flux linkage
is proportional to current (in inductors), etc.
• All the components must be bilateral, meaning that the
current is the same amount for opposite polarities of the
source voltage.
• Passive components may be used. These are components
such as resistors, capacitors, and inductors, that do not
amplify or rectify.
• Active components may not be used. Active components
include transistors, semiconductor diodes, and electron
tubes. Such components are never bilateral and seldom
linear.

3. Procedure for applying Superposition
Theorem
Circuits Containing Only Independent Sources:-
• Consider only one source to be active at a time.
• Remove all other ideal voltage sources by short circuit & all
other ideal current sources by open circuit.
Voltage source
is replaced by a
Short Circuit
Current source is
replaced by a
Open Circuit

4. • If there are practical sources, replace them by the
combination of ideal source and an internal
resistances.
• After that, short circuit the ideal voltage source &
open circuit the ideal current source..

5. Example :1
R1
R2
R3
V1 V2
100 W 20 W
10 W
15 V 13 V
R1 R2
R3
V1
100 W 20 W
10 W
15 V
V2 shorted
REQ = 106.7 W, IT = 0.141 A and IR3
= 0.094 A

6. R1 R2
R3
V1 V2
100 W 20 W
10 W
15 V 13 V
REQ = 29.09 W, IT = 0.447 A and IR3
= 0.406 A
R1 R2
R3
V2
100 W 20 W
10 W
13 V
V1 shorted
Example :1

7. R1 R2
V1 V2
100 W 20 W15 V 13 V
Adding the currents gives IR3
= 0.5 A
REQ = 106.7 W, IT = 0.141 A and IR3
= 0.094 A
REQ = 29.09 W, IT = 0.447 A and IR3
= 0.406 A
With V2 shorted
With V1 shorted
0.094 A 0.406 A
Example :1

8. R1 R2
R3
V1 V2
100 W 20 W
10 W
15 V 13 V
With 0.5 A flowing in R3, the voltage across R3 must
be 5 V (Ohm’s Law). The voltage across R1 must
therefore be 10 volts (KVL) and the voltage across R2
must be 8 volts (KVL). Solving for the currents in R1
and R2 will verify that the solution agrees with KCL.
0.5 A
IR1
= 0.1 A and IR2
= 0.4 A
IR3
= 0.1 A + 0.4 A = 0.5 A
Example :1

9. Procedure for applying Superposition
Theorem
 Circuits Containing Independent & Dependent
Sources :-
• Consider only one source to be active at a time.
• Remove all other ideal independent voltage sources by
short circuit & all other ideal independent current sources
by open circuit - as per the original procedure of
superposition theorem.
• NEITHER SHORT CIRCUIT NOR OPEN CIRCUIT THE
DEPENDENT SOURCE. LEAVE THEM INTACT AND AS THEY
ARE.

10. • Dependent Current Source:-
A current source whose parameters are controlled by
voltage/current else where in the system
v = αVx
VDCS
(Voltage Dependent
Current source)
v = βix
CDCS
(Current Dependent
Current source)
• Dependent Voltage Source:-
v = µVx
VDVS
(Voltage Dependent
Voltage source)
v = ρix
CDVS
(Current Dependent
Voltage source)
A voltage source whose parameters are controlled by
voltage/current else where in the system

11. 11
Example :3
Find i0 in the circuit shown below. The circuit involves a dependent source. The
current may be obtained as by using superposition as :
''
0
'
00 iii 
i’
0 is current due to 4A current source
i’’
0 is current due to 20V voltage source

12. 12
To obtain i’
0we short circuit the 20V
sources
i1
i2
i3A.4i1 
0)(152)(3 320
'
212  iiiiii
For loop 2
For loop 1
For loop 3
045)(1)(5 3
'
02313  iiiiii
310 iii' 
For solving i1, i2, i3 A
17
52
i 0
'


13. 13
To obtain i’’
0 , we open circuit the 4A sources
i4
i5
05ii6i ''
054 
For loop 4
052010i- ''
054  ii
For loop 5
A
17
60
i ''
0 
For solving i4 and i5
A
17
8
17
60
17
52
iiiTherefore, ''
0
'
00



5
''
0 ii 

14. THANK
YOU