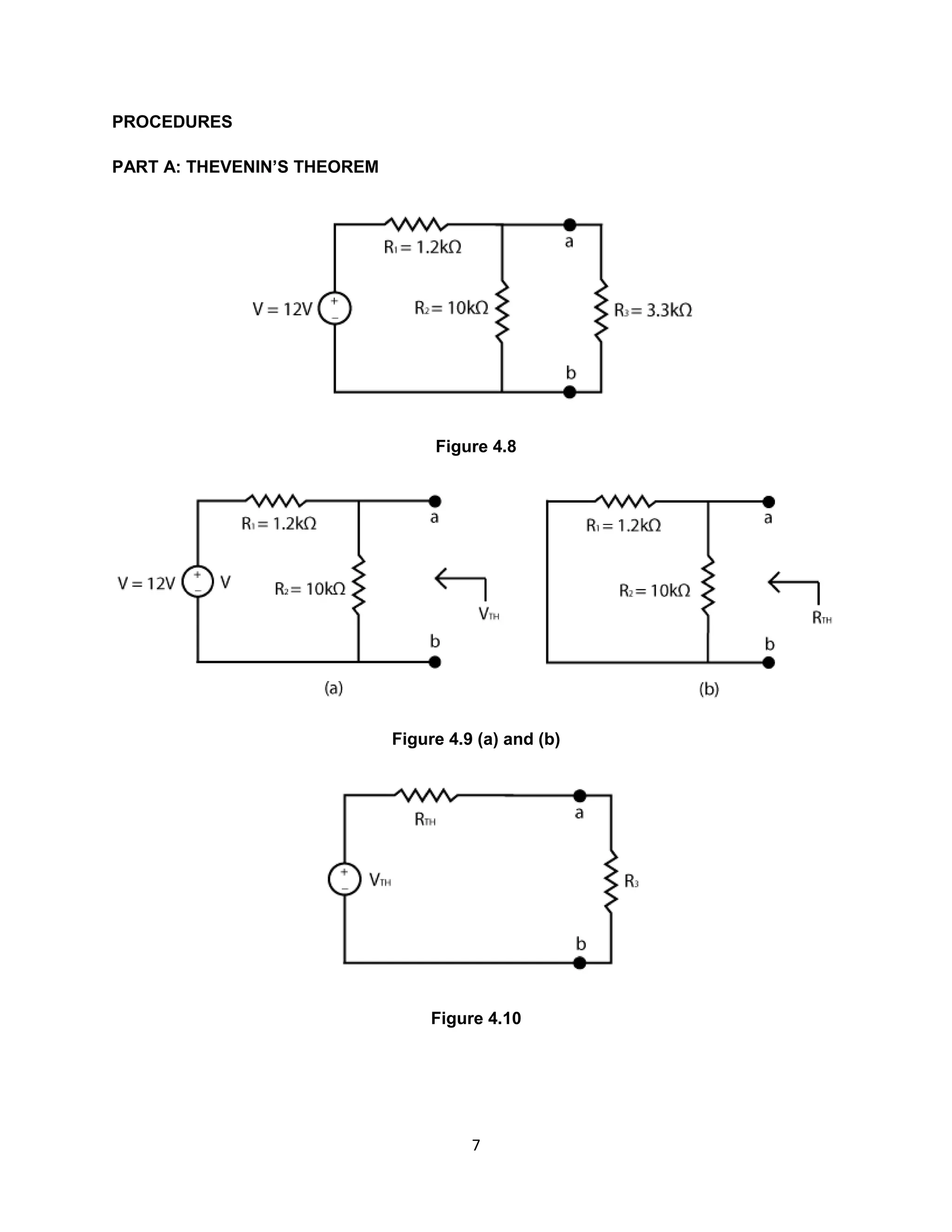
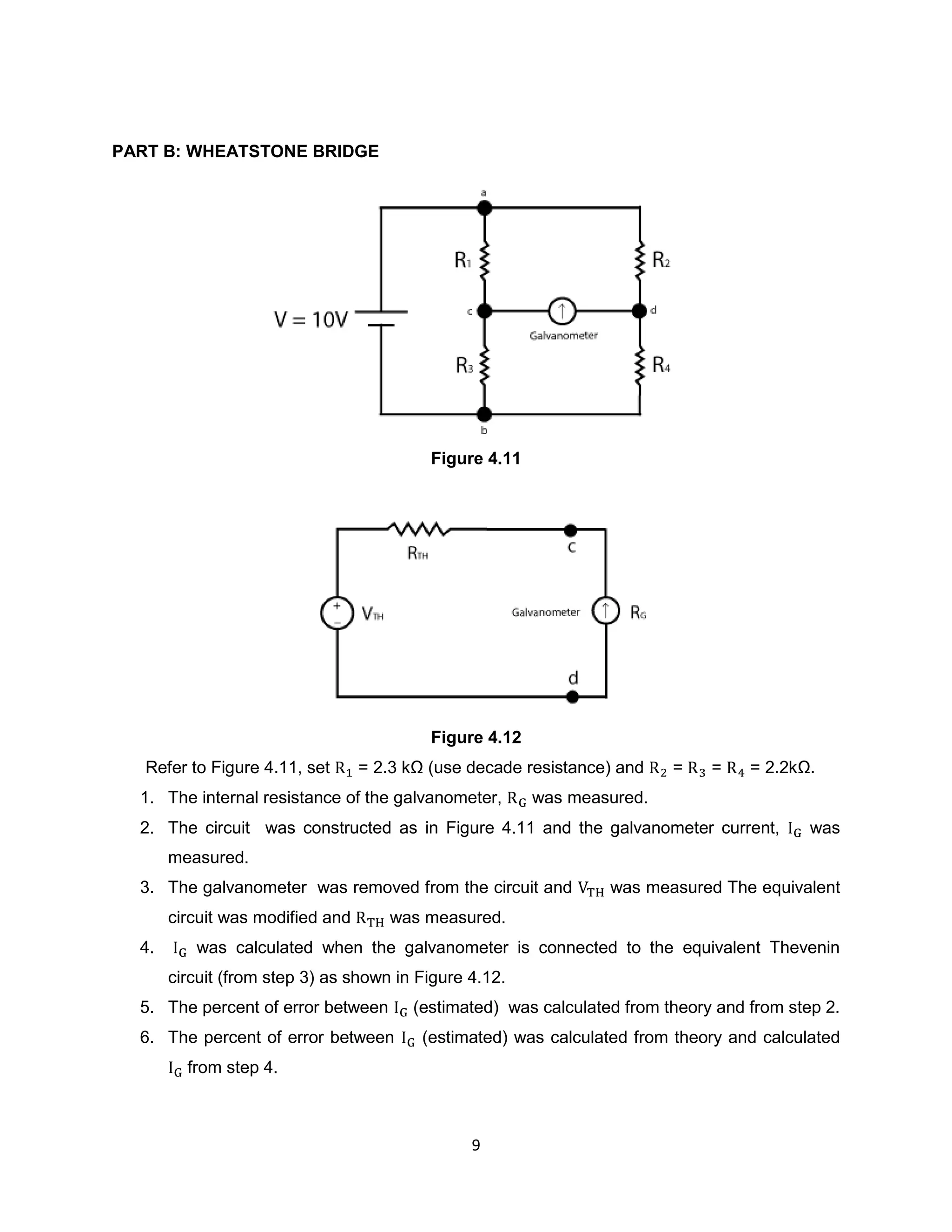
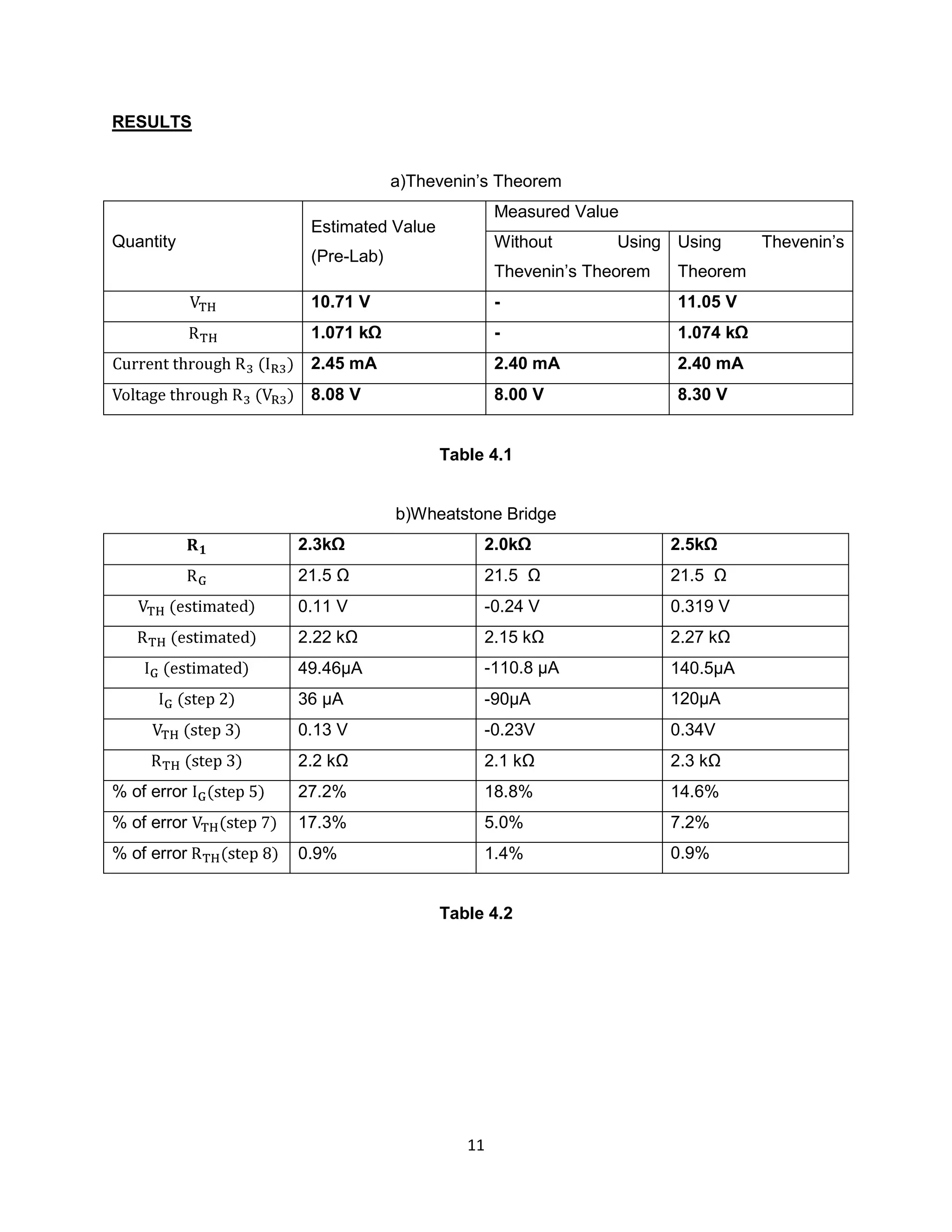
1) The document describes an experiment to analyze DC resistive circuits using Thevenin's Theorem and analyze an unbalanced Wheatstone bridge. 2) Key aspects of the experiment include using Thevenin's Theorem to determine equivalent resistance (Rth) and voltage (Vth) for circuits, and analyzing how these values change when measuring a Wheatstone bridge circuit with an unknown resistance. 3) Results showed differences between estimated and measured values for currents and voltages due to experimental errors like resistance in connecting wires. Thevenin's Theorem was useful for simplifying complex circuits into equivalent components.

1. (EEE230)
EXPERIMENT 4
THEVENIN’S THEOREM AND WHEATSTONE BRIDGE
OBJECTIVES
1. To analyze DC resistive circuits using Thevenin‟s Theorem.
2. To analyze an unbalanced Wheatstone bridge using Thevenin‟s Theorem.
LIST OF REQUIREMENTS
Equipments
1. DC power supply.
2. Galvanometer.
3. Digital multimeter.
4. Analogue multimeter.

2. Components
1. Resistor: 2.2kΩ, 1.2kΩ, 10kΩ, 3.3kΩ
2. Decade resistance.
THEORY
INTRODUCTION
In this experiment, we have learned about the Thevenin‟s Theorem and Wheatstone bridge.
Firstly, we have learned how to analyze DC resistive circuits using Thevenin‟s Theorem.
Secondly, we also have learned how to analyze an unbalanced Wheatstone bridge using
Thevenin‟s Theorem. Lastly, we have learned how to calculate the value of and using
Thevenin‟s Theorem.
THEVENIN’S THEOREM
1

3. Thevenin‟s Theorem states that a linear two-terminal circuit can be replaced by an equivalent
circuit consisting of a voltage source in series with a resistor , where is the open-
circuit voltage at the terminals and is the input or equivalent resistance at the terminals
when the independent sources are turned off.
Steps On Calculating , and
Figure 4.1 : Thevenin Equivalent Voltage
or Thevenin Equivalent Voltage is the value of voltage from point „a‟ and point „b‟. Note that
no current flows through , so there is no voltage drop across . To calculate the value, we
can use the equation 1.1.
(Equation 1.1)
2

4. Figure 4.2 : Thevenin Equivalent Resistance
or Thevenin Equivalent Resistance value can be found by calculating the value using the
equation 1.2.
(equation 1.2)
3

5. Figure 4.3
To find , first we have to reattach R between to „a‟ and „b‟, put in series with R and place
on the circuit as in Figure 4.3. Then calculate the current through R using the equation 1.3.
(equation 1.3)
To find voltage across R, use this equation 1.4.
(equation 1.4)
4

6. WHEATSTONE BRIDGE
The most accurate measurements of resistance are made with a galvanometer (or a voltmeter)
in a circuit called a Wheatstone bridge, named after the British physicist Charles Wheatstone.
This circuit consists of three known resistances and an unknown resistance connected in a
diamond pattern.
A DC voltage is connected across two opposite points of the diamond, and a
galvanometer is bridged across the other two points. When all four of the resistances bear a
fixed relationship to each other, the currents flowing through the two arms of the circuit will be
equal, and no current will flow through the galvanometer. By varying the value of one of the
known resistances, the bridge can be made to balance for any value of unknown resistance,
which can then be calculated from the values of the other resistors.
A Wheatstone bridge is a measuring instrument which is used to measure an unknown
electrical resistance by balancing the resistances in the two branches of a bridge circuit, one
branch of which includes the unknown resistance.
Figure 4.4
5

7. In the circuit shown in Figure 4.4, let be the unknown resistance and , and
are resistances of known value and the resistance of is adjustable. If the ratio of the two
resistances in the lower branch is equal to the ratio of the two unknown legs ,
then the output voltage between the two midpoints will be zero and no current will flow
between the midpoints. is varied until this condition is reached. Then,
If is the impressed voltage, then current and
Voltage at A,
Voltage at B,
Now to have the voltage difference between A & B to be zero, =0
VA = VB
Detecting zero current can be done to extremely high accuracy. Therefore, if , and
are known to high precision, then can be measured to high precision. Very small changes
in disrupt the balance and are readily detected.
Alternatively, if , and are known, but is not adjustable, and the impressed
voltage is known, then the voltage or current flow through the midpoints can be used to
calculate value of . This setup is frequently used in strain gauge measurements, as it is
usually faster to read a voltage level off a meter than to adjust a resistance to zero the voltage.
6

8. PROCEDURES
PART A: THEVENIN’S THEOREM
Figure 4.8
Figure 4.9 (a) and (b)
Figure 4.10
7

9. 1. The circuit in Figure 4.8 was connected.
2. The current through and the voltage across was measured. The
results was recorded in Table 4.1 (without using Thevenin‟s Theorem).
3. was removed and was connected in the circuit as in Figure 4.9(a) (Figure 4.8 with
removed). The voltage across point „a‟ and „b‟ was measured and recorded it as
.
4. The cirdcuit was construct as in Figure 4.9(b) (Figure 4.8 with removed and the 12 V
source replaced by a short circuit). The resistance at point „a‟ and „b‟ was measured and
recorded it as .
5. The circuit was constructed as in Figure 4.10. A resistor for was obtained as close
as possible to its value using decade box.
6. The current through and the voltage across in the circuit of Figure 4.10 was
measured. The result was recorded in Table 4.1.
7. The percent of error between (estimated) was calculated from theory with from
step 3.
8. The percent of error between (estimated) was calculated from theory with from
step 4.
9. The percent of error between (estimated) was calculated from theory with using
Thevenin‟s Theorem and without using Thevenin‟s Theorem.
10. The percent of error between (estimated) was calculated from theory with using
Thevenin‟s Theorem and without using Thevenin‟s Theorem.
8

10. PART B: WHEATSTONE BRIDGE
Figure 4.11
Figure 4.12
Refer to Figure 4.11, set = 2.3 kΩ (use decade resistance) and = = = 2.2kΩ.
1. The internal resistance of the galvanometer, was measured.
2. The circuit was constructed as in Figure 4.11 and the galvanometer current, was
measured.
3. The galvanometer was removed from the circuit and was measured The equivalent
circuit was modified and was measured.
4. was calculated when the galvanometer is connected to the equivalent Thevenin
circuit (from step 3) as shown in Figure 4.12.
5. The percent of error between (estimated) was calculated from theory and from step 2.
6. The percent of error between (estimated) was calculated from theory and calculated
from step 4.
9

11. 7. The the percent of error between (estimated) was calculated from theory with
from step 3.
8. The the percent of error between (estimated) was calculated from theory with
from step 3.
9. Step 1 to 8 for = 2.0 kΩ and 2.5kΩ was repeated and the results was recorded in
Table 4.2.
10

12. RESULTS
a)Thevenin‟s Theorem
Measured Value
Estimated Value
Quantity Without Using Using Thevenin‟s
(Pre-Lab)
Thevenin‟s Theorem Theorem
10.71 V - 11.05 V
1.071 kΩ - 1.074 kΩ
2.45 mA 2.40 mA 2.40 mA
8.08 V 8.00 V 8.30 V
Table 4.1
b)Wheatstone Bridge
2.3kΩ 2.0kΩ 2.5kΩ
21.5 Ω 21.5 Ω 21.5 Ω
0.11 V -0.24 V 0.319 V
2.22 kΩ 2.15 kΩ 2.27 kΩ
49.46µA -110.8 µA 140.5µA
36 µA -90µA 120µA
0.13 V -0.23V 0.34V
2.2 kΩ 2.1 kΩ 2.3 kΩ
% of error 27.2% 18.8% 14.6%
% of error 17.3% 5.0% 7.2%
% of error 0.9% 1.4% 0.9%
Table 4.2
11

13. Discussion
For part A, Thevenin‟s Theorem states that in order for us to find the current flows
through a resistor R which connected across any two points „a‟ and „b‟ of an active network is by
dividing the potential difference between „a‟ and „b‟ (with R disconnected) by R+r, where r is the
resistance of the network measured between „a‟ and „b‟ when R disconnected and the sources
of E.M.F has been replaced by their values of internal resistance.
The value of and need to be measured using Thevenin Theorem since the
resistor R was disconnected from the circuit.So there are no current flows through resistor
.and no voltage drop at .
From the result,The value of and expected is slightly different from the
measured value and The value for and without using and using Thevenin‟s Theorem and
the expected values are also different because while conducting this experiment ,there might
have some errors.Maybe this error occur because we using connecting wires.In connecting
wires it have some resistance values so it will affect our final values.From the table 4.1,the value
with using Thevenin‟s Theorem are a bit higher than without using Thevenin‟s Theorem .It
can show us that connecting wires have resistance values since we use more connecting wires
when want measure without using Thevenin‟s theorem than using thevenin‟s theorem
circuit.
Based on the Table 4.2 ,We can see that galvanometer has internal resistance.That
means it can affect our final measured Values.The Values of VTH,RTH and IG estimate is
different with measured values.As in experiment part A.The connecting wires has resistance
values that affect our measured Values.From the calculated percent error of VTH,RTH and IG
,We can see the how big the error occur,For the VTH and IG the error is high because some
error while connecting the circuit as the example the decade resistor box maybe have some
internal resistance that affect our values.While the RTH the error is not too high .As in this
experiment we was using Analogue multimeter to measure VTH an IG so the parallax error can
be occurs since our eyes sometimes does not perpendicular toward the scale of analogue
meter.So we need make sure the scale is perpendicular toward our eyes.
12

14. To Measure RTH by using Thevenin‟s Theorem we need to make sure all DC voltage is
removed from the circuit or short circuit.It is because we need pure of resistance since when
voltage flow on the resistance it will affect the reading of RTH. To measure VTH and IG we can
just put the measure probe to point “c” and “d” as in Figure 4.11 without change the original
condition of the loads in the circuit.
13

15. CONCLUSION
After doing the experiment, we can conclude that by using Thevenin‟s Theorem, we can
analyze DC resistive circuit and analyze an unbalanced Wheatstone bridge circuit. We also
know that without using Thevenin‟s Theorem, we could not find , , and in a very
complex circuit .Thevenin‟s Theorem is very important in circuit analysis. It helps us to simplify a
large circuit by replacing the circuit into a single independent source and a single resistor. This
replacement technique is very useful in circuit design.This lab is also effectively showed how the
Wheatstone bridge provides a mechanism to calculate an unknown resistance using the known
relationships given through the resistivity correlation to length. It demonstrated how to set-up a
Wheatstone bridge and how to construct a Wheatstone bridge in a laboratory setting.As in this
experiment we can measure the , , and IG by using Thevenin‟s theorem.We can
measure IG and VTH by connecting the measure probe to complete circuit but for RTH we need to
make sure no DC voltage flows in the circuit to follow the Thevenin‟s Theorem rules.
14

16. REFERENCES
1. Alexander, C.K., & Sadiku, M.N.O. (2004). Fundamentals of Electric Circuits : Fourth
Edition. New York: McGraw Hill.
2. http://www.megaessays.com
3. Rusnani Ariffin & Mohd Aminudin Murad (2011).Laboratory Manual Electrical
Engineering Laboratory 1:University Publication Center (UPENA).
4. http://www.allaboutcircuits.com/vol_1/chpt_10/8.html
5. http://www.efunda.com/designstandards/sensors/methods/wheatstone_bridge.cfm
15