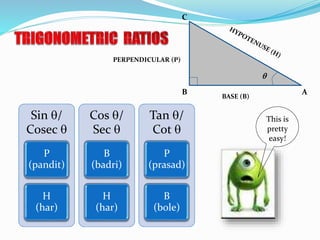
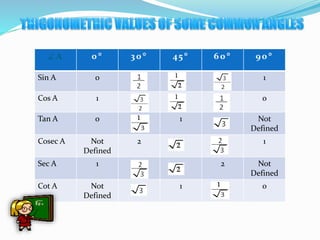
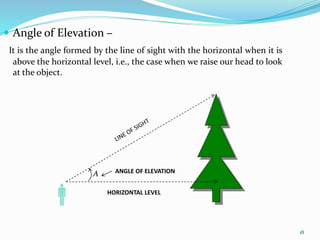
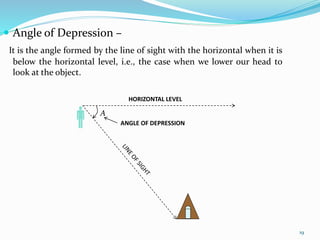
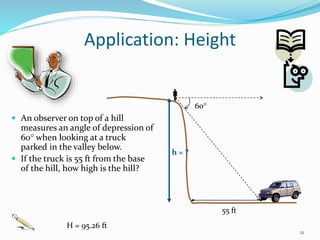
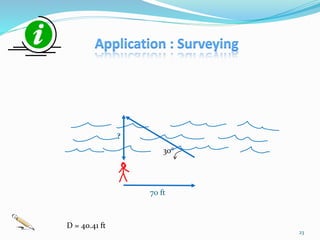
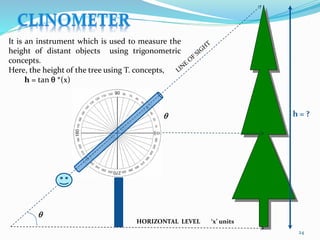
The document is a PowerPoint presentation on the introduction to trigonometry for 10th-grade students, outlining key concepts, historical background, and applications of trigonometry in various fields such as architecture, astronomy, and geology. It explains trigonometric ratios, identities, and methodologies for teaching the topic, along with practical applications like measuring heights and distances. The presentation emphasizes the importance of trigonometry in both academic and real-world contexts, including problem-solving and critical thinking skills.