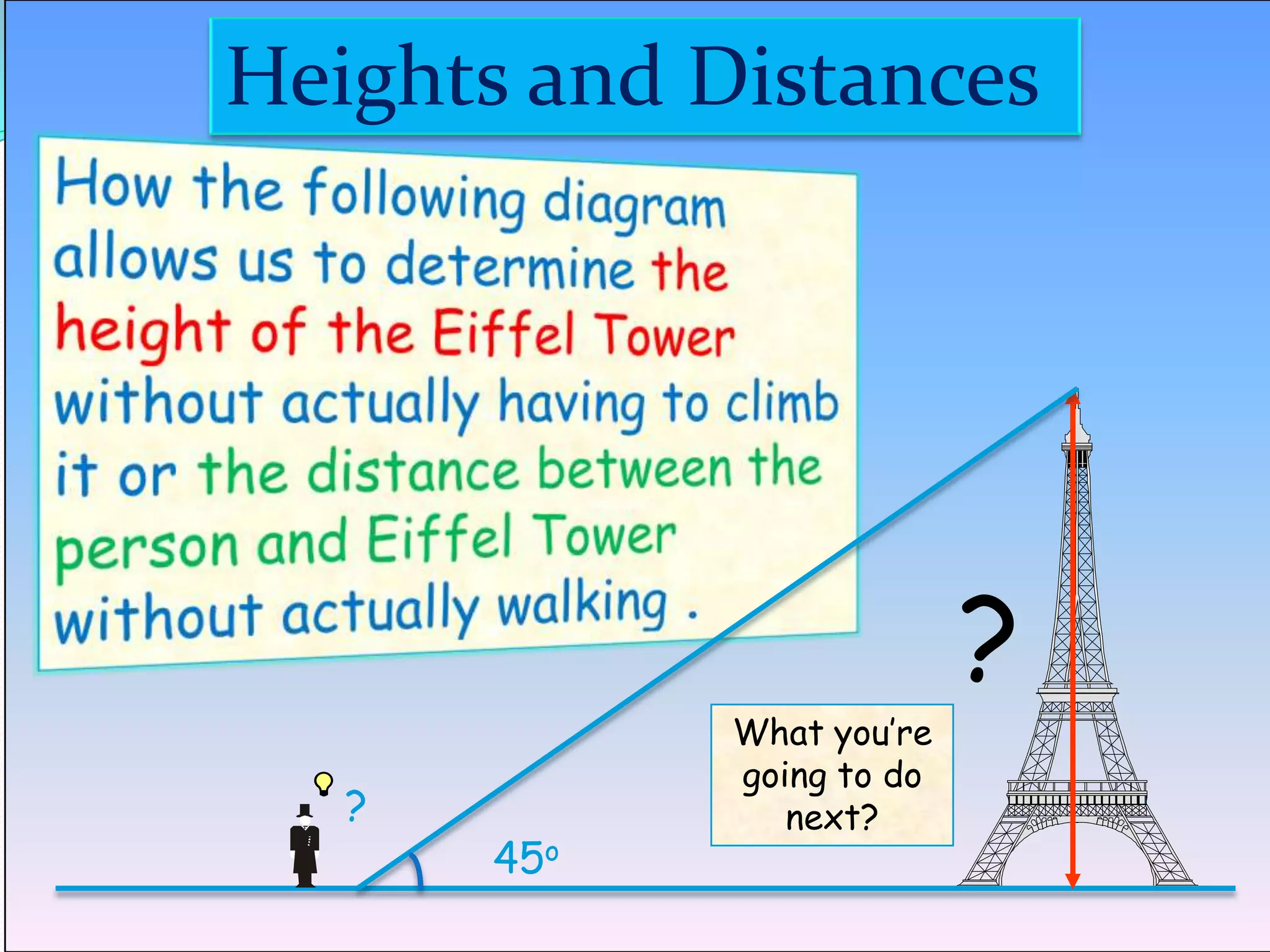
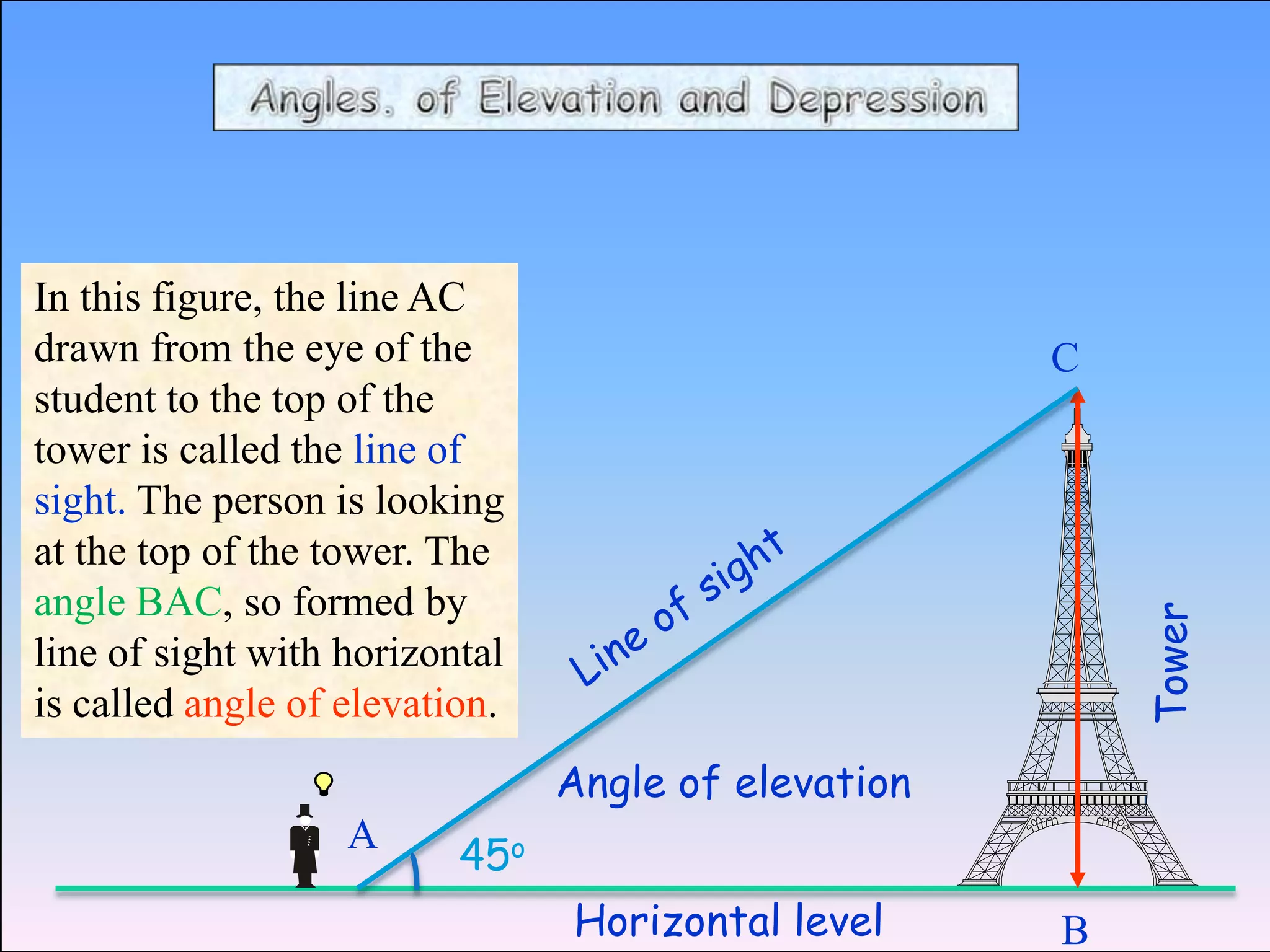
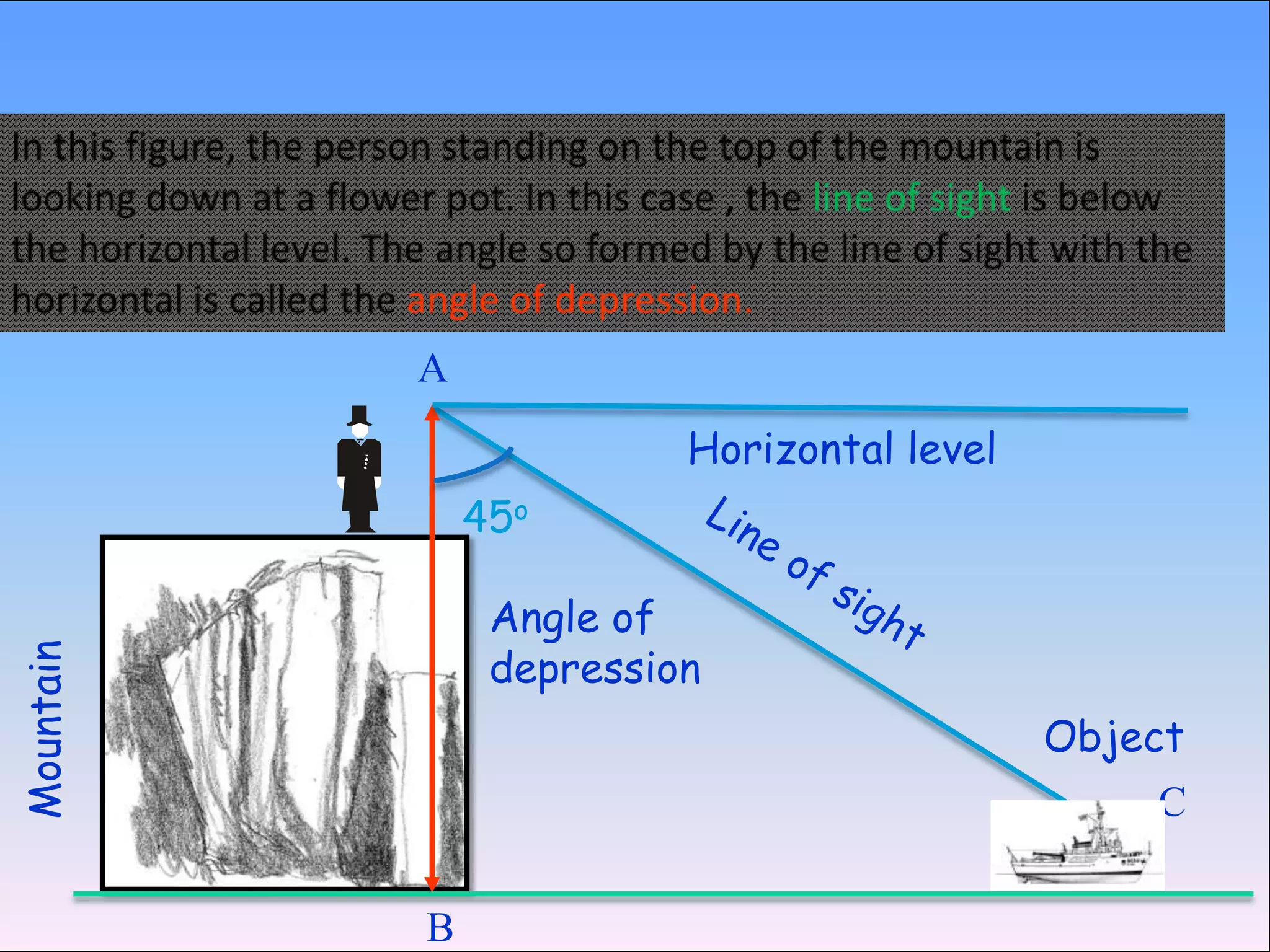
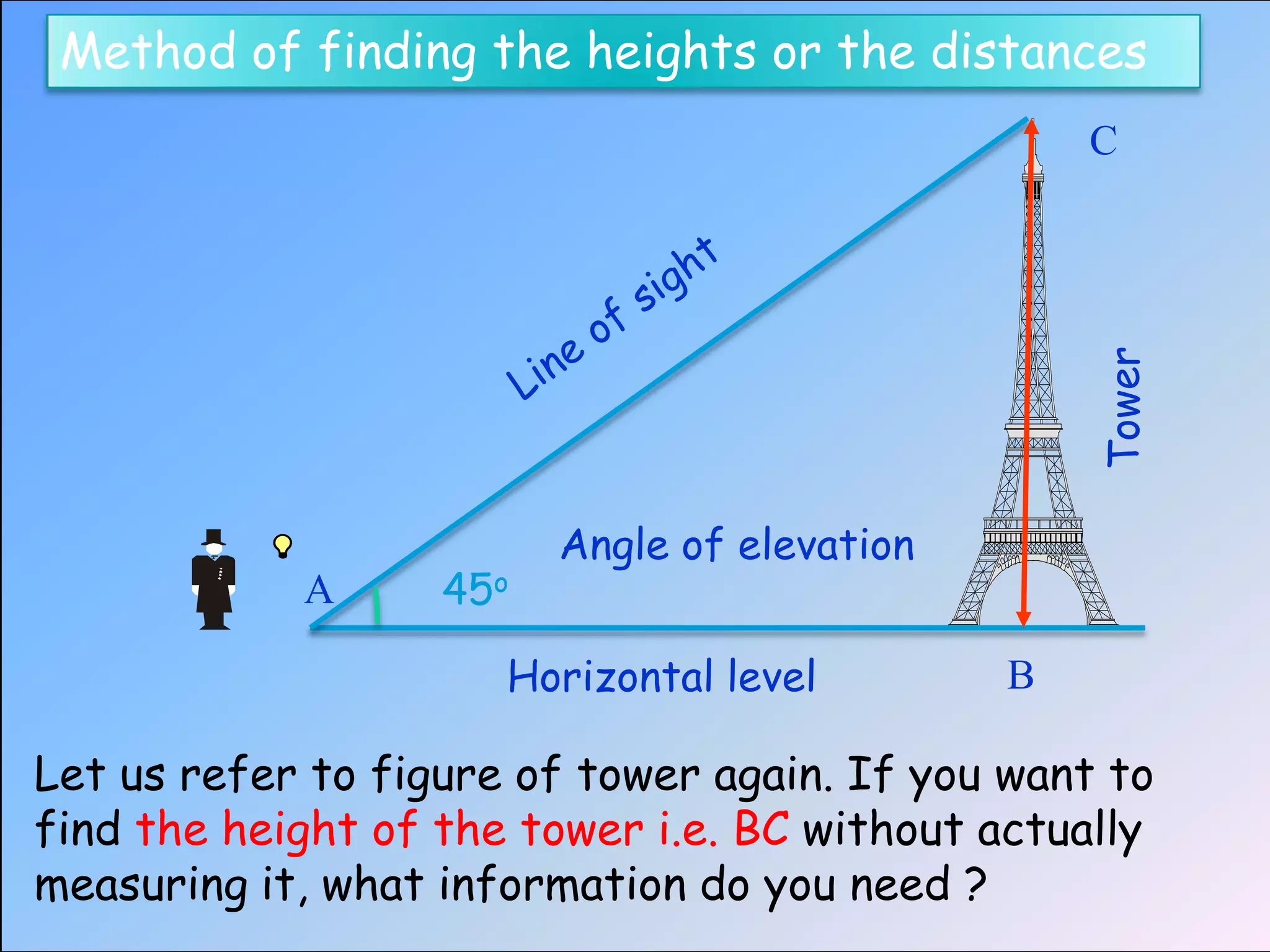
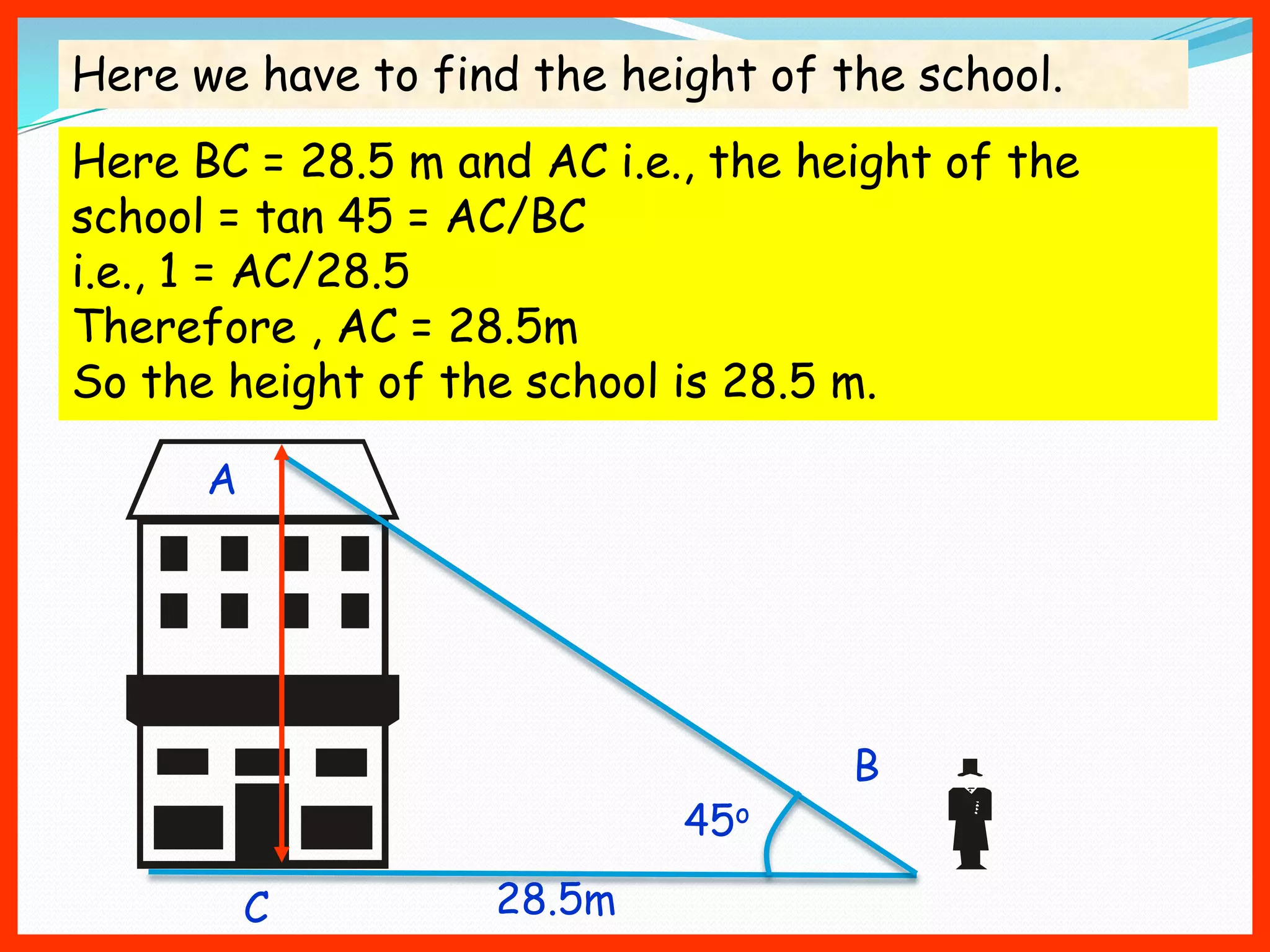
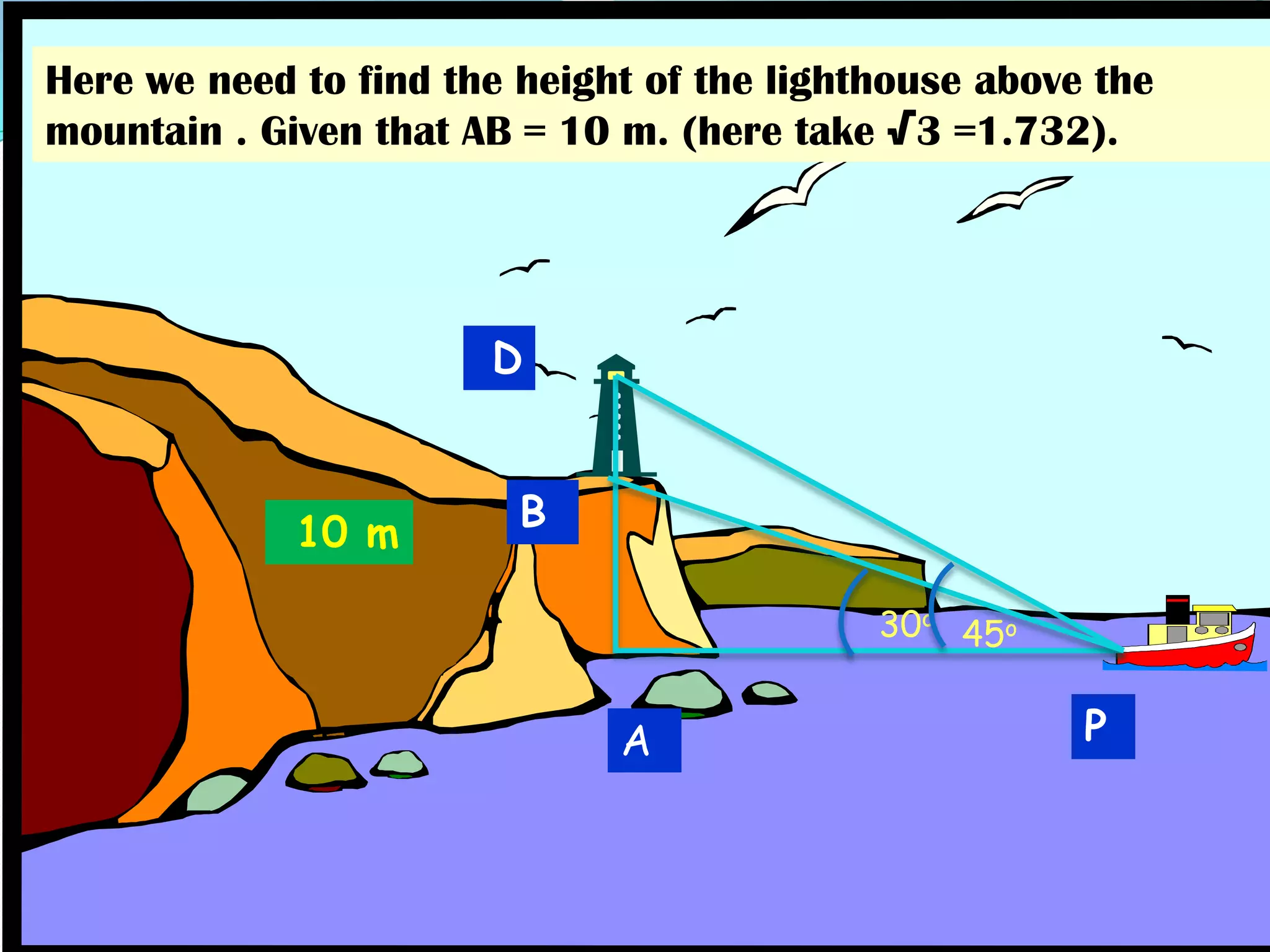
Trigonometry is used to calculate unknown heights, distances, and angles using relationships between sides and angles of triangles. It was developed by ancient Greek mathematicians like Thales and Hipparchus to solve problems in astronomy and geography. Some key applications include using trigonometric ratios like tangent and cotangent along with known distances and angles of elevation/depression to determine the height of objects like towers, buildings, and mountains when direct measurement is not possible. The document provides historical context and examples to illustrate how trigonometric concepts have been applied to problems involving finding heights, distances, and other unknown measurements through the use of triangles and their properties.

1. PRANAY
RAJPUT
X-B

2. Heights and Distances
?
What you’re
going to do
? next?
45o

3. In this situation , the distance or the heights can
be founded by using mathematical techniques,
which comes under a branch of ‘trigonometry’.
The word ‘ trigonometry’ is derived from the
Greek word ‘tri’ meaning three , ‘gon’ meaning
sides and ‘metron’ meaning measures.
Trigonometry is concerned with the relationship
between the angles and sides of triangles. An
understanding of these relationships enables
unknown angles and sides to be calculated
without recourse to direct measurement.
Applications include finding heights/distances of
objects.

6. Trigonometry
An early application of trigonometry was made by Thales on a
visit to Egypt. He was surprised that no one could tell him the
height of the 2000 year old Cheops pyramid. He used his
Thales of Miletus knowledge of the relationship between the heights of objects
640 – 546 B.C. The
first Greek and the length of their shadows to calculate the height for
Mathematician. He them. (This will later become the Tangent ratio.) Can you see what
predicted the Solar
Eclipse of 585 BC. this relationship is, based on the drawings below?
h 480 ft
720 ft
Similar Similar 6 ft
Triangles Triangles
9 ft
Sun’s rays casting shadows mid-afternoon Sun’s rays casting shadows late afternoon
Thales may not have used similar triangles directly to solve the problem but
h
he knew that6the ratio of the 6x 720 horizontal sides of each triangle was
vertical to
h 480 ft sun. Can you use the
constant and unchanging for different heights of the (Egyptian feet of course)
720 9 9
measurements shown above to find the height of Cheops?

7. Later, during the Golden Age of Athens (5 BC.), the philosophers and
mathematicians were not particularly interested in the practical side of
mathematics so trigonometry was not further developed. It was another 250 years
or so, when the centre of learning had switched to Alexandria (current day Egypt)
that the ideas behind trigonometry were more fully explored. The astronomer and
mathematician, Hipparchus was the first person to construct tables of
trigonometric ratios. Amongst his many notable achievements was his
determination of the distance to the moon with an error of only 5%. He used the
diameter of the Earth (previously calculated by Eratosthenes) together with
angular measurements that had been taken during the total solar eclipse of March
190 BC.
Eratosthenes Hipparchus of Rhodes
275 – 194 BC 190-120 BC

8. Early Applications of Trigonometry
Finding the height of a
mountain/hill.
h
25o 20o
x d
Constructing sundials to Finding the distance to
estimate the time from the moon.
the sun’s shadow.

9. Historically trigonometry was developed for work in
Astronomy and Geography. Today it is used
extensively in mathematics and many other areas of
the sciences.
•Surveying
•Navigation
•Physics
•Engineering

10. In this figure, the line AC
drawn from the eye of the C
student to the top of the
tower is called the line of
sight. The person is looking
at the top of the tower. The
angle BAC, so formed by
Tower
line of sight with horizontal
is called angle of elevation.
Angle of elevation
A
45o
Horizontal level B

11. A
Horizontal level
45o
Angle of
depression
Mountain
Object
C
B

12. Method of finding the heights or the distances
C
Tower
Angle of elevation
A 45o
Horizontal level B
Let us refer to figure of tower again. If you want to
find the height of the tower i.e. BC without actually
measuring it, what information do you need ?

13. We would need to know the following:
i. The distance AB which is the distance between
tower and the person .
ii. The angle of elevation angle BAC .
Assuming that the above two conditions are given then
how can we determine the height of the height of the
tower ?
In ∆ABC, the side BC is the opposite side in
relation to the known angle A. Now, which of the
trigonometric ratios can we use ? Which one of them
has the two values that we have and the one we need to
determine ? Our search narrows down to using either
tan A or cot A, as these ratios involve AB and BC.
Therefore, tan A = BC/AB or cot A = AB/BC, which
on solving would give us BC i.e., the height of the tower.

14. Some Applications
of trigonometry
based on finding
heights and
distance

15. Here we have to find the height of the school.
Here BC = 28.5 m and AC i.e., the height of the
school = tan 45 = AC/BC
i.e., 1 = AC/28.5
Therefore , AC = 28.5m
So the height of the school is 28.5 m.
A
B
45o
C 28.5m

16. Here we have to find the length of the ladder in the
below figure and also how far is the foot of the ladder
from the house ? (here take √3 = 1.73m)
Now, can you think trigonometric
ratios should we consider ?
It should be sin 60
So, BC/AB = sin 60 or 3.7/AB =
√3/2 B
Therefore BC = 3.7 x 2/√3
Hence length of the ladder is
4.28m
Now BC/AC = cot 60 = 1/√3
3.7m
i.e., AC = 3.7/√3 = 2.14m (approx)
60o
Therefore the foot of the
ladder from the house is 2.14m. A C

17. Here we need to find the height of the lighthouse above the
mountain . Given that AB = 10 m. (here take √3 =1.732).
D
10 m B
30o 45o
A P

18. Since we know the height of the mountain
is AB so we consider the right ∆PAB. We
have tan 30 = AB/AP i.e., 1/√3 = 10/AP
therefore AP = 10√3m so the distance of
the building = 10√3m = 17.32m
Let us suppose DB = (10+x)m now in
right ∆PAD tan 45 = AD/AP = 10+x/10√3
therefore 1 = 10+x/10√3 i.e., x = 10(√3-1)
=7.32. So, the length of the flagstaff is
7.32m

19. Summary
 The line of sight is the line drawn from the eye of
the observer to the point in the object viewed by
the observer.
 The angle of elevation of an object viewed, is the
angle formed by the line of sight with the horizontal
when it is above the horizontal level, i.e., the case
when we raise our head to look at the object.
 The angle of depression of an object viewed, is the
angle formed by the line of sight with the horizontal
when it is below the horizontal level , i.e., the case
when we lower our the head to look at the object.
 The height or length of an object or the distance
between two distant objects can be determined with
the help of trigonometric ratios.

20. Thank you