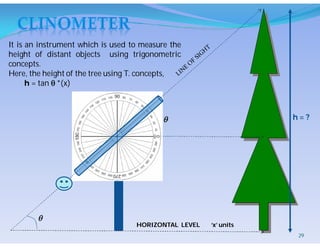
This project aims to provide a comprehensive understanding of trigonometry, emphasizing its history, significance, and applications across various fields such as astronomy, physics, and engineering. It details key concepts and identities related to trigonometric ratios, as well as practical applications like measuring distances and heights. The project was created by Debdita Pan under the supervision of Smt. Tapasi Paul Chowdhury, highlighting collaborative efforts in its completion.

1. 1

2. This project has been made with the aim of providing basic understanding on
the subject – TRIGONOMETRY . Sincere efforts have been made to make the
presentation a unique experience to the viewer. Stress has been laid on the
appearance, neatness and quality of the presentation. No effort has been spared
to make the reading and understanding of the presentation complete and
interesting. I have tried to do my best and hope that the project of mine would
be appreciated by all.
Supervised by – Smt Tapasi Paul Chowdhury
Created by – Debdita Pan
Roll no :116
Teacher Education Department
Scottish Church College
2

3. One cannot succeed alone no matter how great one’s abilities are,
without the cooperation of others. This project, too, is a result of efforts
of many. I would like to thank all those who helped me in making this
project a success.
I would like to express my deep sense of gratitude to my Maths Teacher,
Mrs. Tapasi Paul Chowdhury who was taking keen interest in our lab
activities and discussed various methods which could be employed
towards this effect, and I really appreciate and acknowledge her pain
taking efforts in this endeavour.
3

4. 4

5. Right Triangle Trigonometry
5

6. What is Trigonometry
The word trigonometry is derived
from Greek words ‘tri’ (meaning
three), ‘gon’ (meaning sides) and
metron (meaning measure). In fact
, The earliest known work on
trigonometry was recorded in Egypt
and Babylon. Early astronomers
used to find out the distance of the
stars and planet s from the Earth.
6

7. WHAT CAN YOU DO WITH
TRIGONOMETRY?
 Historically, it was developed for astronomy and geography,
but scientists have been using it for centuries for other
purposes, too. Besides other fields of mathematics,
trigonometry is used in physics, engineering, and chemistry.
Within mathematics, trigonometry is used primarily in
calculus (which is perhaps its greatest application), linear
algebra, and statistics. Since these fields are used throughout
the natural and social sciences, trigonometry is a very useful
subject to know.
7

8.  Some historians say that trigonometry was
invented by Hipparchus, a Greek mathematician.
He also introduced the division of a circle into
360 degrees into Greece.
 Hipparchus is considered the greatest
astronomical observer, and by some the greatest
astronomer of antiquity. He was the first Greek
to develop quantitative and accurate models for
the motion of the Sun and Moon. With his solar
and lunar theories and his numerical
trigonometry, he was probably the first to
develop a reliable method to predict solar
eclipses.
8

9. The first use of the idea of ‘sine’ in the way
we use it today was in the work
‘Aryabhatiyam’ by Aryabhatta, in A.D. 500.
Aryabhatta used the word ardha-jiva for the
half-chord, which shortened to jya or jiva.
When it was translated into Latin, the word
jiva was translated into sinus, which means
curve.
Sin
Sin
Sin
Sin
Sin
Sin
Sin
Sin
Sin
Sin
Sin
Sin
Sin
Sin
Sin
Sin
ORIGIN OF ‘SINE’
9

10. Foundation of COSINE & TANGENT
The origin of terms cosine and tangent was much
later. The cosine function arose from the need to
compute the sine of the complementary angle.
Aryabhata called it kotijya. The name cosinus
originated with Edmund Gunter. In 1674, the English
mathematician Sir Jonas Moore first use the
abbreviated notation cos.
10

11. The trigonometric ratios of the angle A in the right triangle
ABC see in fig.
•Sin of A =side opposite to angle A =BC
hypotenuse AC
•Cosine of A =side adjacent to angle A =AB
hypotenuse AC
•Tangent of A =side opposite to angle A =BC
side adjacent to angle A AB
C
A B 11

12. Cosecant of A = 1 = hypotenuse = AC
sin of A side opposite to angle A BC
Secant of A = 1 = hypotenuse = AC
sin of A side adjacent to angle a AB
Cotangent of A= 1 =side adjacent to angle A= AB
tangent of A side opposite to angle A BC
C
A B 12

13. B A
C
Sin /
Cosec 
P
(pandit)
H
(har)
Cos /
Sec 
B
(badri)
H
(har)
Tan /
Cot 
P
(prasad)
B
(bole)
This is
pretty
easy!
BASE (B)
PERPENDICULAR (P)

13

14. WHAT ARE
TRIGONOMETRIC
IDENTITIES ????
An equation involving trigonometric ratios
of an angle is called a Trigonometric
Identitity, if it is true for all values of the
angle(s) involved. Trigonometric identities
are ratios and relationships between
certain trigonometric functions.
14

15.  A 0  3 0  45  60  90 
Sin A 0 1
Cos A 1 0
Tan A 0 1 Not
Defined
Cosec A Not
Defined
2 1
Sec A 1 2 Not
Defined
Cot A Not
Defined
1 0
15

16. Sin2  + Cos2  = 1
• 1 – Cos2  = Sin2 
• 1 – Sin2  = Cos2 
Tan2  + 1 = Sec2 
• Sec2  - Tan2  = 1
• Sec2  - 1 = Tan2 
Cot2  + 1 = Cosec2 
• Cosec2  - Cot2  = 1
• Cosec2  - 1 = Cot2 
16

17. OTHER USEFUL IDENTITIES
Sin θ = 1/cosec θ
Cos θ = 1/sec θ
Tan θ = 1/cot θ
Cosec θ = 1/sin θ
Sec θ = 1/cos θ
Tan θ = 1/cot θ
17

18. Applications
 Measuring inaccessible lengths
 Height of a building (tree, tower, etc.)
 Width of a river (canyon, etc.)
18

19.  Angle of Elevation –
It is the angle formed by the line of sight with the horizontal when it is
above the horizontal level, i.e., the case when we raise our head to look
at the object.

A
HORIZONTAL LEVEL
ANGLE OF ELEVATION
19

20.  Angle of Depression –
It is the angle formed by the line of sight with the horizontal when it is
below the horizontal level, i.e., the case when we lower our head to
look at the object.
 A
HORIZONTAL LEVEL
ANGLE OF DEPRESSION
20

21. Application: Height
 To establish the height of a
building, a person walks 120 ft
away from the building.
 At that point an angle of
elevation of 32 is formed when
looking at the top of the
building.
32
120 ft
h = ?
Example 1 of 4
H = 74.98 ft
21

22. Application: Height
 An observer on top of a hill
measures an angle of depression of
68 when looking at a truck
parked in the valley below.
 If the truck is 55 ft from the base
of the hill, how high is the hill?

68
h = ?
55 ft
Example 2 of 4
H = 136.1 ft
22

23. 23

24. ?
70 ft
37
Example 3 of 4
D = 52.7 ft
24

25. h = ?
HORIZONTAL LEVEL


It is an instrument which is used to measure the
height of distant objects using trigonometric
concepts.
Here, the height of the tree using T. concepts,
h = tan  *(x)
‘x’ units
25

26. The angle of elevation of the top of a tower from a
point on the ground, which is 30 m away from the
foot of the tower is 30°. Find the height of the tower
Let AB be the tower and the angle of elevation from point C
(on ground) is
30°.
In ΔABC,
.
Therefore, the height of the tower is
26

27. A circus artist is climbing a 20 m long rope, which is tightly
stretched and tied from the top of a vertical pole to the
ground. Find the height of the pole, if the angle made by
the rope with the ground level is 30 °.
Sol:- It can be observed from the figure that AB is the pole.
In ΔABC,
Therefore, the height of the pole is 10 m.
27

28. Home Assignment
 A ladder 15 m long just reaches the top of a vertical wall. If the
ladder makes an angle of 60°with the wall, find the height of the
wall ? (7.5 √3 )
 A pole 12 m high casts a shadow 4 √3 m long on the ground.
Find the angle of elevation ? (60°)
 The angle of elevation of the top of a tower from a point on the
ground is 30° if on walking 30m towards the tower, the angle of
elevation becomes 60°.Find the height of the tower ?(15√3 )
 An observer 1.5m tall is 20.5m away from a tower 22m high.
Determine the angle of elevation of the top of the tower from the
eye of the observer ? (45°)
 If the length of the shadow cast by a pole be times the length of
the pole, find the angle of elevation of the sun. [ 30o ]
28

29. h = ?
HORIZONTAL LEVEL


It is an instrument which is used to measure the
height of distant objects using trigonometric
concepts.
Here, the height of the tree using T. concepts,
h = tan  *(x)
‘x’ units
29

30. Jantar Mantar
observatory
For millenia, trigonometry
has played a major role in
calculating distances
between stellar objects and
their paths.
30

31. Trigonometry begins in the right triangle, but it doesn’t have to be restricted
to triangles. The trigonometric functions carry the ideas of triangle
trigonometry into a broader world of real-valued functions and wave forms.
Trig functions are the relationships amongst various sides in right triangles.
The enormous number of applications of trigonometry include astronomy,
geography, optics, electronics, probability theory, statistics, biology, medical
imaging (CT scans and ultrasound), pharmacy, seismology, land surveying,
architecture.
I get it!
31