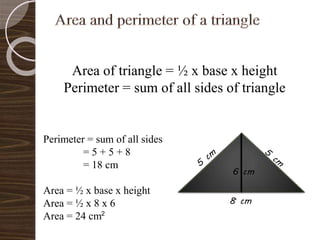
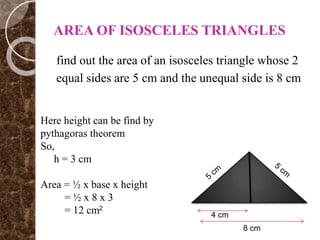
The document discusses Heron's formula for calculating the area of a triangle. Heron's formula uses the lengths of the three sides of a triangle to calculate its area, rather than requiring the base and height. The formula is defined as the square root of s(s-a)(s-b)(s-c), where s is the semi-perimeter (half the perimeter) and a, b, c are the three side lengths. The formula is useful when it is difficult to measure the base and height of a triangle directly. An example problem demonstrates calculating the area of a triangle with side lengths 3cm, 4cm, and 5cm using Heron's formula.

1. CHAPTER - 12
HERON’S FORMULA
By- Aditya Khurana

2. INTRODUCTION
 In earlier classes we have studied to find an
area and perimeter of a triangle
 Perimeter is sum of all sides of the given
triangle
 Area is equal to the total portion covered in a
triangle

3. Area of triangle = ½ x base x height
Perimeter = sum of all sides of triangle
8 cm
Perimeter = sum of all sides
= 5 + 5 + 8
= 18 cm
Area = ½ x base x height
Area = ½ x 8 x 6
Area = 24 cm
6 cm
2

4. TYPES OF TRIANGLES
EQUILATERAL TRIANGLE
ISOSCELES TRIANGLE
RIGHT ANGLE TRIANGLE
SCALENE TRIANGLE

5. AREA OF RIGHT ANGLE TRIANGLE
In a right angle triangle we can directly apply the
formula to find the area of the triangle, as two
sides containing the right angle as base and height.
8cm
5 cm
Consider the following figure –
Base = 5 cm
Height = 8 cm
Area = ½ x 8 x 5
= 20 cm2

6. AREA OF EQUILATERAL TRIANGLE
Find the area of an equilateral triangle with side10
cm.
5 cm
Here, we can find height by
pythagoras theorem
So here height = √75 = 5√3
Area = ½ x base x height
= ½ x 10 x 5√3
= 25√3 cm2

7. AREA OF ISOSCELES TRIANGLES
find out the area of an isosceles triangle whose 2
equal sides are 5 cm and the unequal side is 8 cm
8 cm
4 cm
Here height can be find by
pythagoras theorem
So,
h = 3 cm
Area = ½ x base x height
= ½ x 8 x 3
= 12 cm2

8. AREA OF TRIANGLE BY HERON’S
FORMULA
Heron was born in about 10AD possibly
in Alexandria in Egypt. His works on
mathematical and physical subjects are
so numerous and varied that he is
considered to be an encyclopedic writer
in these fields. His geometrical works
deal largely with problems on
mensuration. He has derived the famous
formula for the area of a triangle in terms
of its three sides. HERON (10AD -
75AD)

9. HERON’S FORMULA
Area of triangle = √s(s-a)(s-b)(s-c)
Where a , b and c are the sides of the
triangle , and s = semi perimeter, i.e., half
of perimeter of the triangle = a + b + c
2
Area of triangle = √s(s-a)(s-b)(s-c)
Where a , b and c are the sides of the
triangle , and s = semi perimeter, i.e., half
of perimeter of the triangle = a + b + c
2

10. IMPORTANCE OF HERON’S
FORMULA
This formula is helpful where it is not
possible to find height of the triangle
easily.
It is also helpful in finding area of
quadrilaterals.

11. Q- Find the area of triangle whose sides are
3cm, 4cm & 5 cm respectively.
Area of triangle = √s(s-a)(s-b)(s-c)
= 3+4+5 = 6
2
Area of triangle = √6(6-3)(6-4)(6-5)
= √ 6 x 3 x 2 x 1 = 6 cm²
As s = a + b + c
2