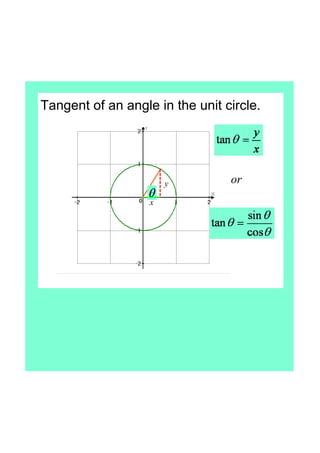
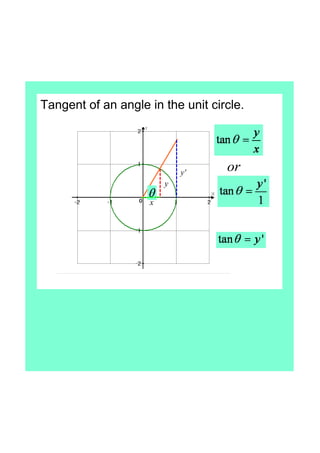
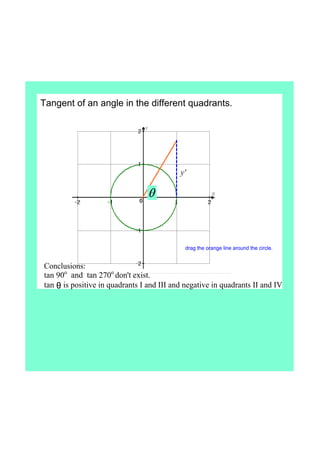
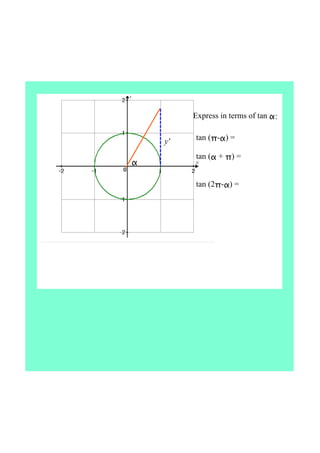
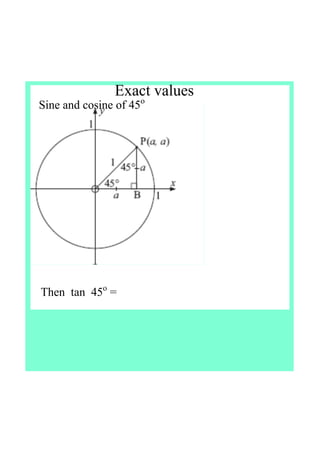
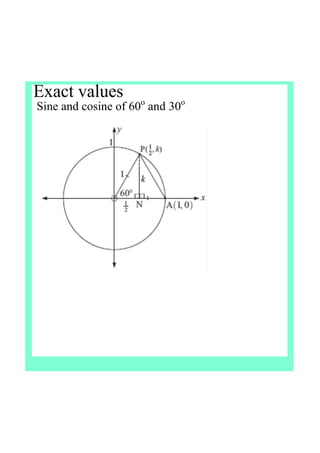
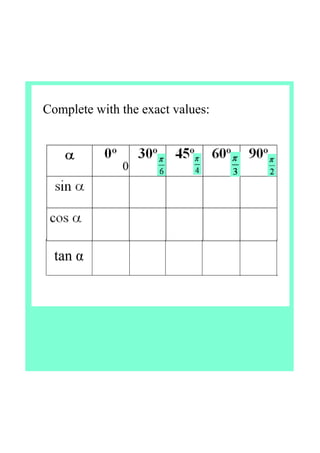
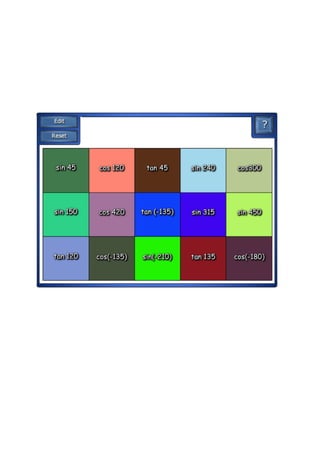
This document defines tangent as the ratio of the opposite to adjacent sides in a right triangle defined by an angle in a unit circle. It finds the exact values of sine, cosine, and tangent for common angles like 45°, 60°, and 30°. The document concludes that tangent is undefined for 90° and 270° and is positive in quadrants I and III and negative in quadrants II and IV.

1. • Define tangent of an angle in the unit circle and in terms of sine and
cosine.
• Find the exact values of sine, cosine and tangent of the most used
angles.
By the end of the lesson you will be able to:
Trigonometry: Exact values of sine and cosine

2. Tangent of an angle in the unit circle.
x
y or

3. Tangent of an angle in the unit circle.
x
y
y' or

4. Tangent of an angle in the different quadrants.
y'
Conclusions:
tan 90o
and tan 270o
don't exist.
tan θ is positive in quadrants I and III and negative in quadrants II and IV
drag the orange line around the circle.

5.
y' tan (π­α) =
tan (α + π) =
tan (2π­α) =
α
Express in terms of tan α:

6. Exact values
Sine and cosine of 45o
Then tan 45o
=

7. Exact values
Sine and cosine of 60o
and 30o

8. Complete with the exact values:
tan α
0

9. tan α
0
0
0
1
1
1

10. Find the exact value of : a) sin 120o

11. Find the exact value of : b) cos 315o

12. Find the exact value of : c) sin

13. Find α , 0 ≤α≤360o
, such that : sin α =

14. Find α , 0 ≤α≤360o
, such that : cos α =

15. Find α , 0 ≤α≤360o
, such that :
cos α =sin α = and