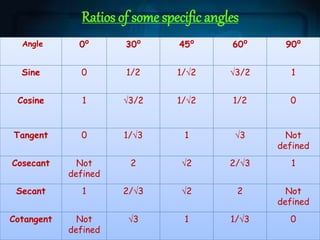
This document provides an introduction to trigonometry. It defines trigonometry as dealing with relations of sides and angles of triangles. It discusses the history of trigonometry and defines the six trigonometric ratios (sine, cosine, tangent, cosecant, secant, cotangent). It provides the ratios for some specific angles and identities relating the ratios. It describes applications of trigonometry in fields like astronomy, navigation, architecture, and more.