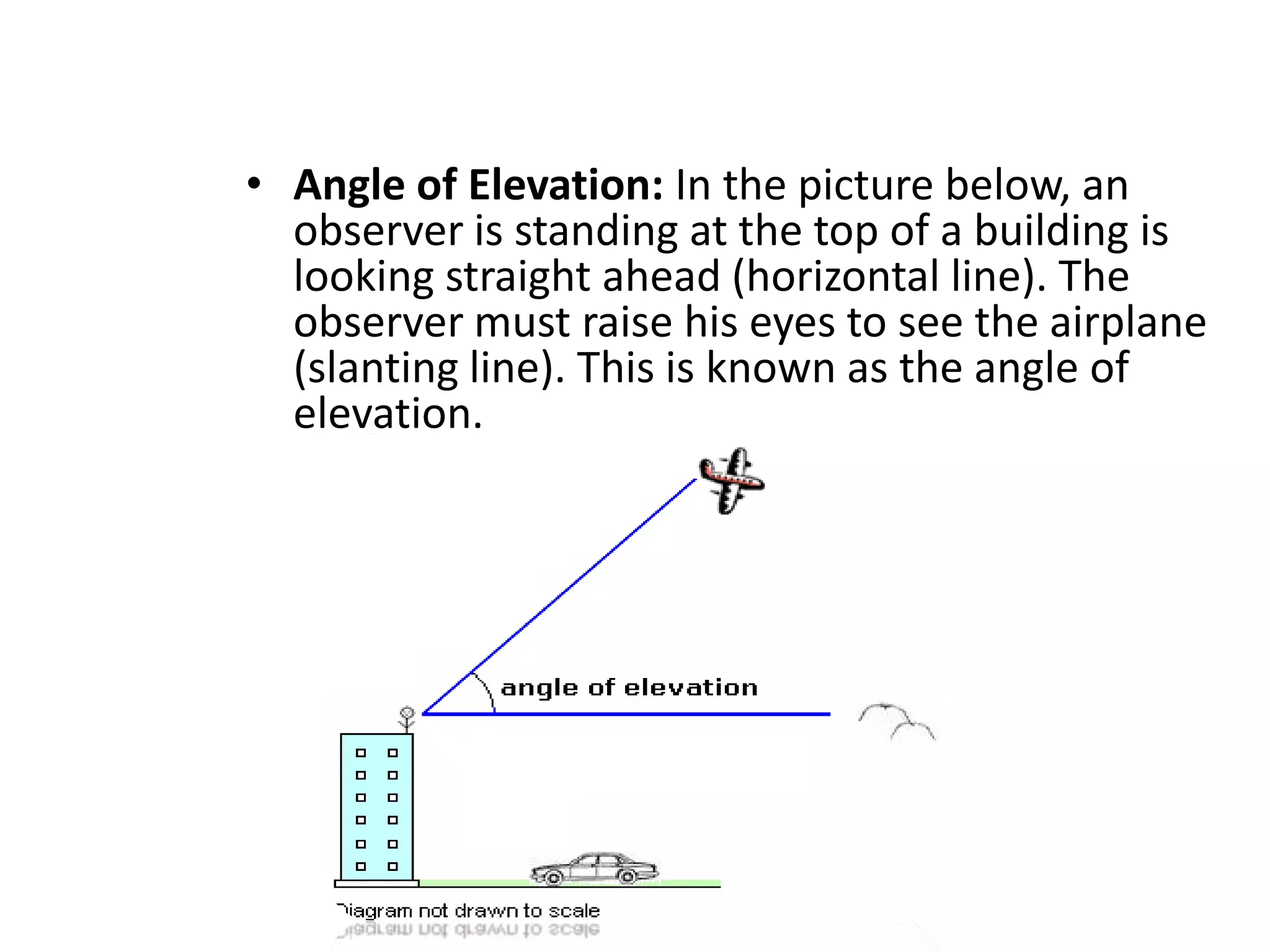
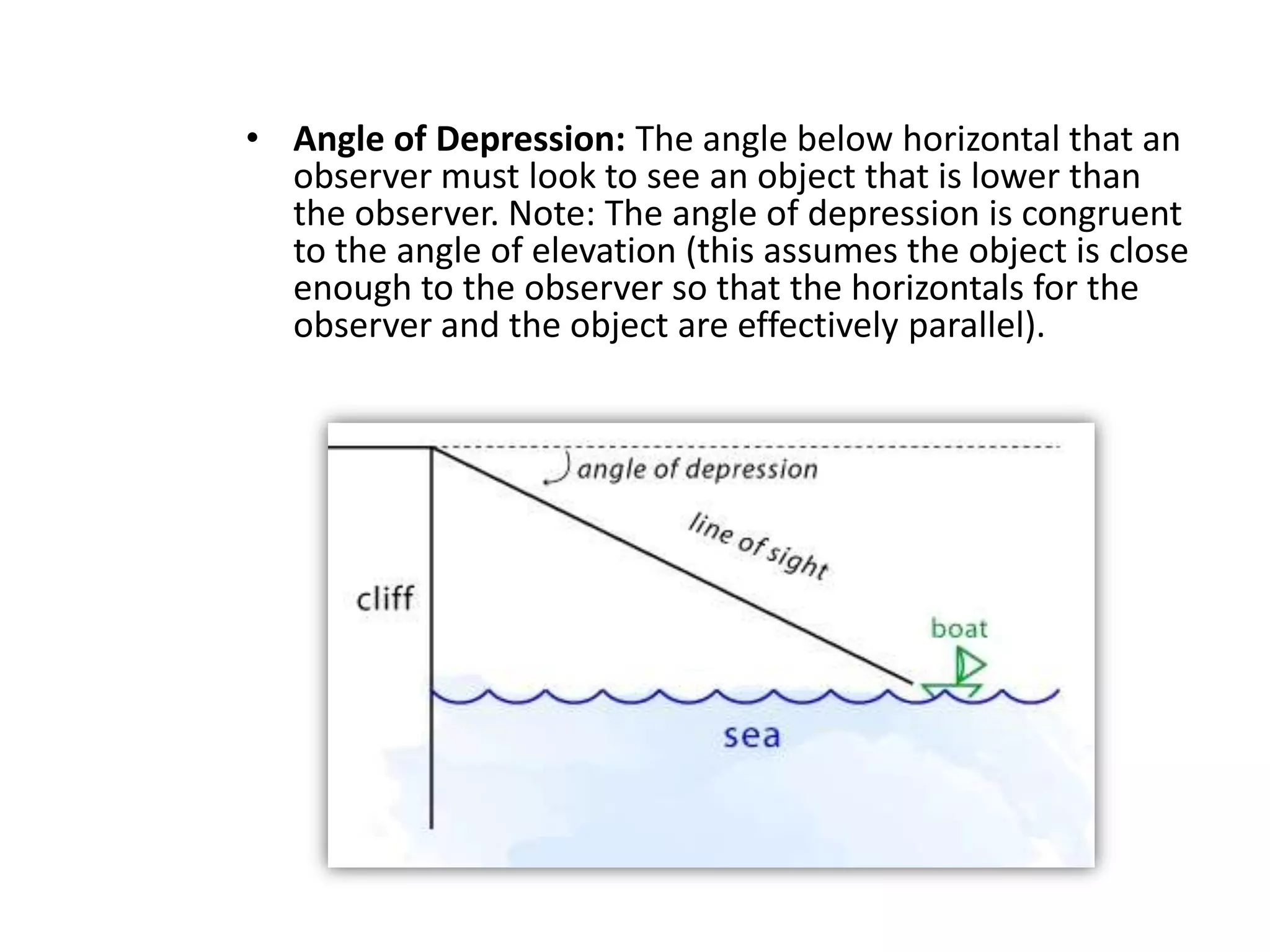
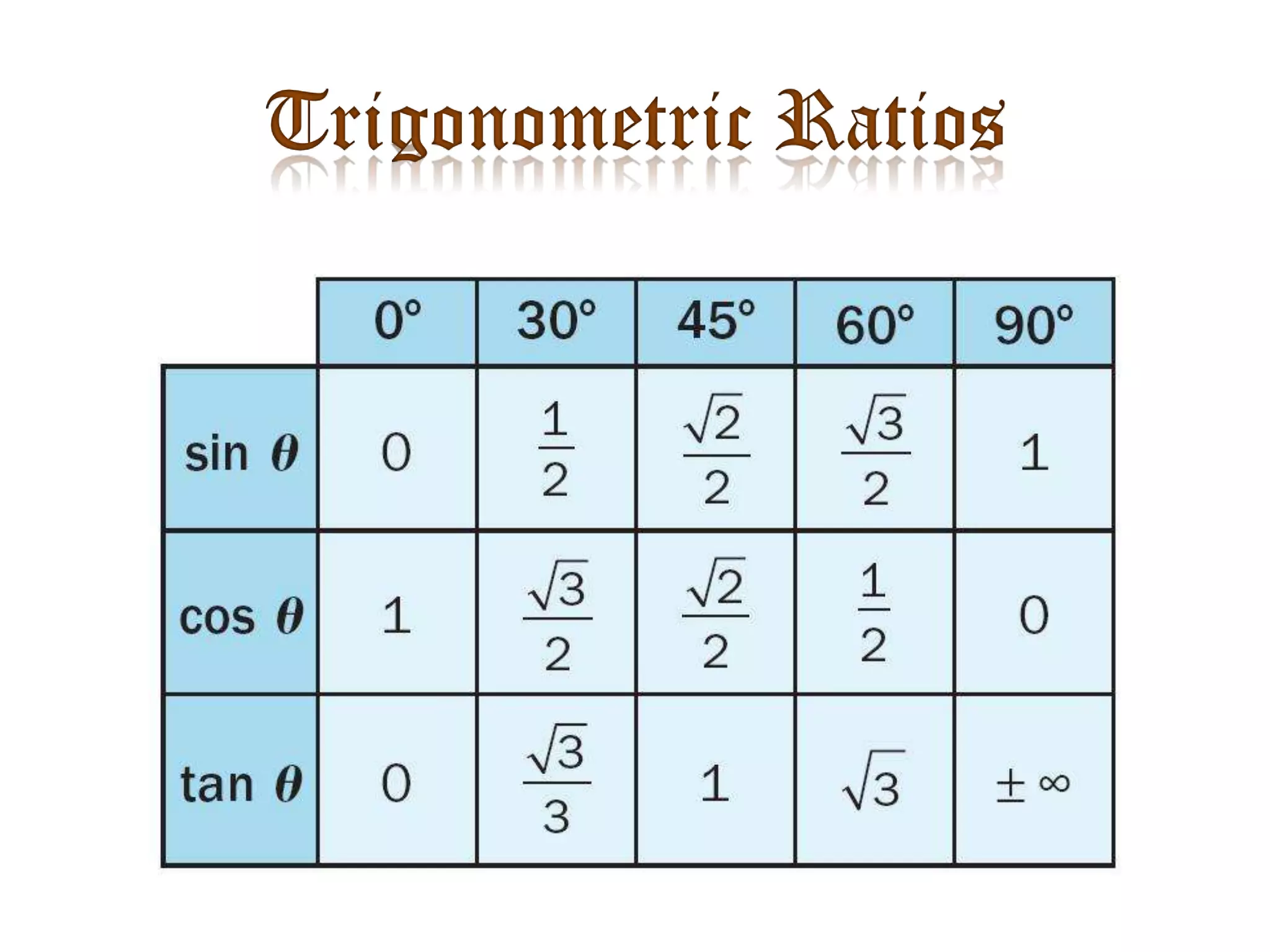
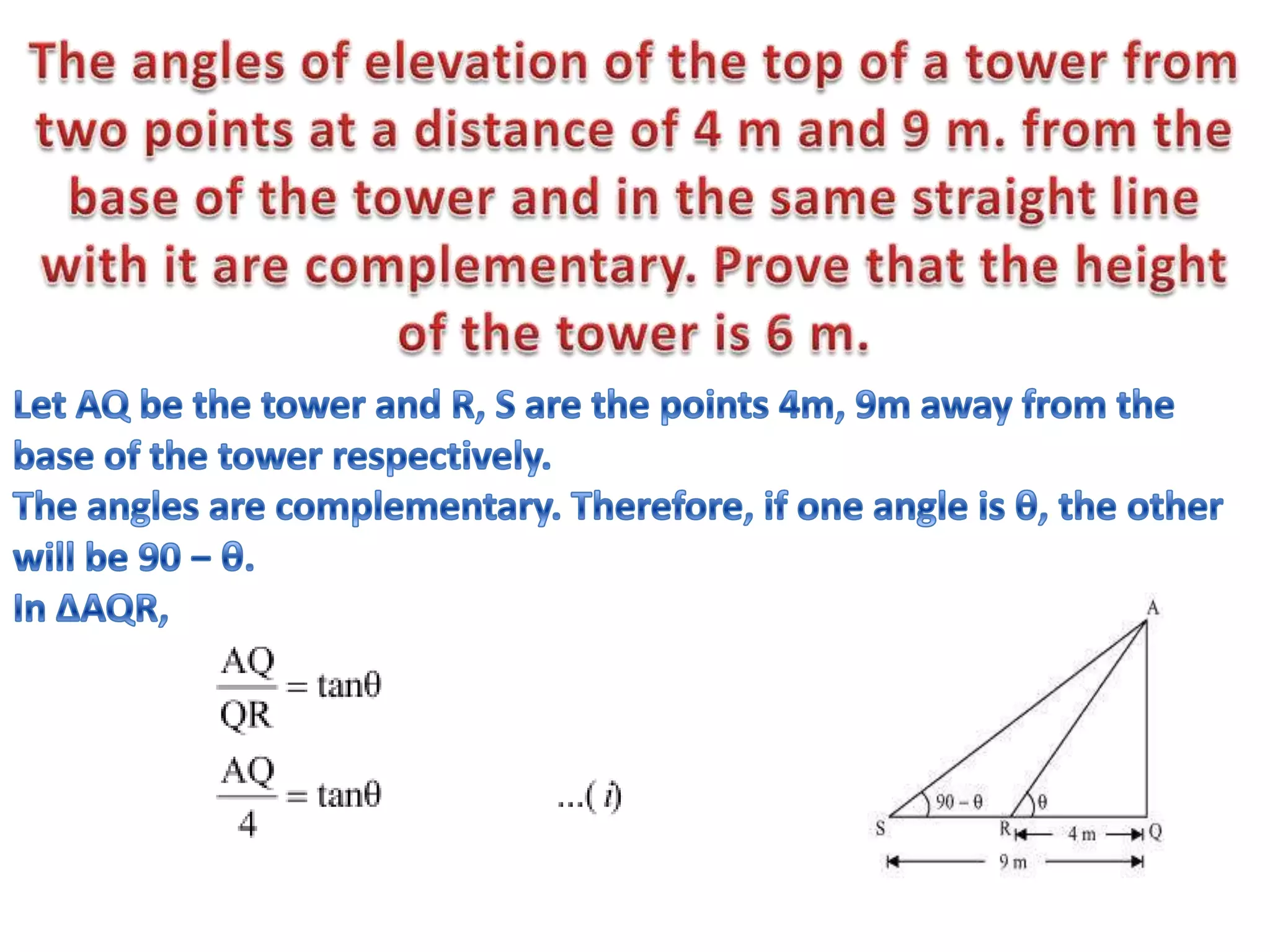
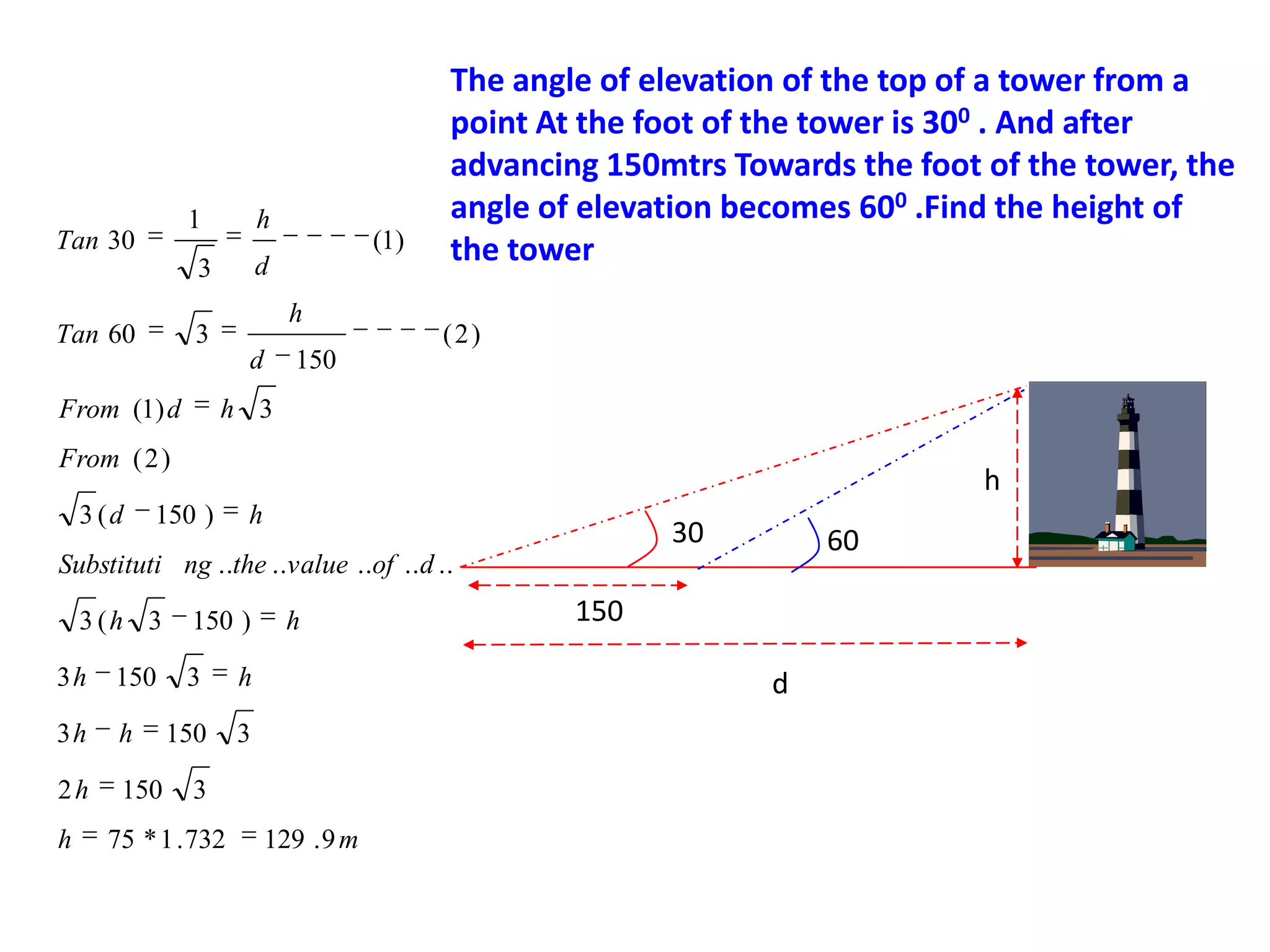
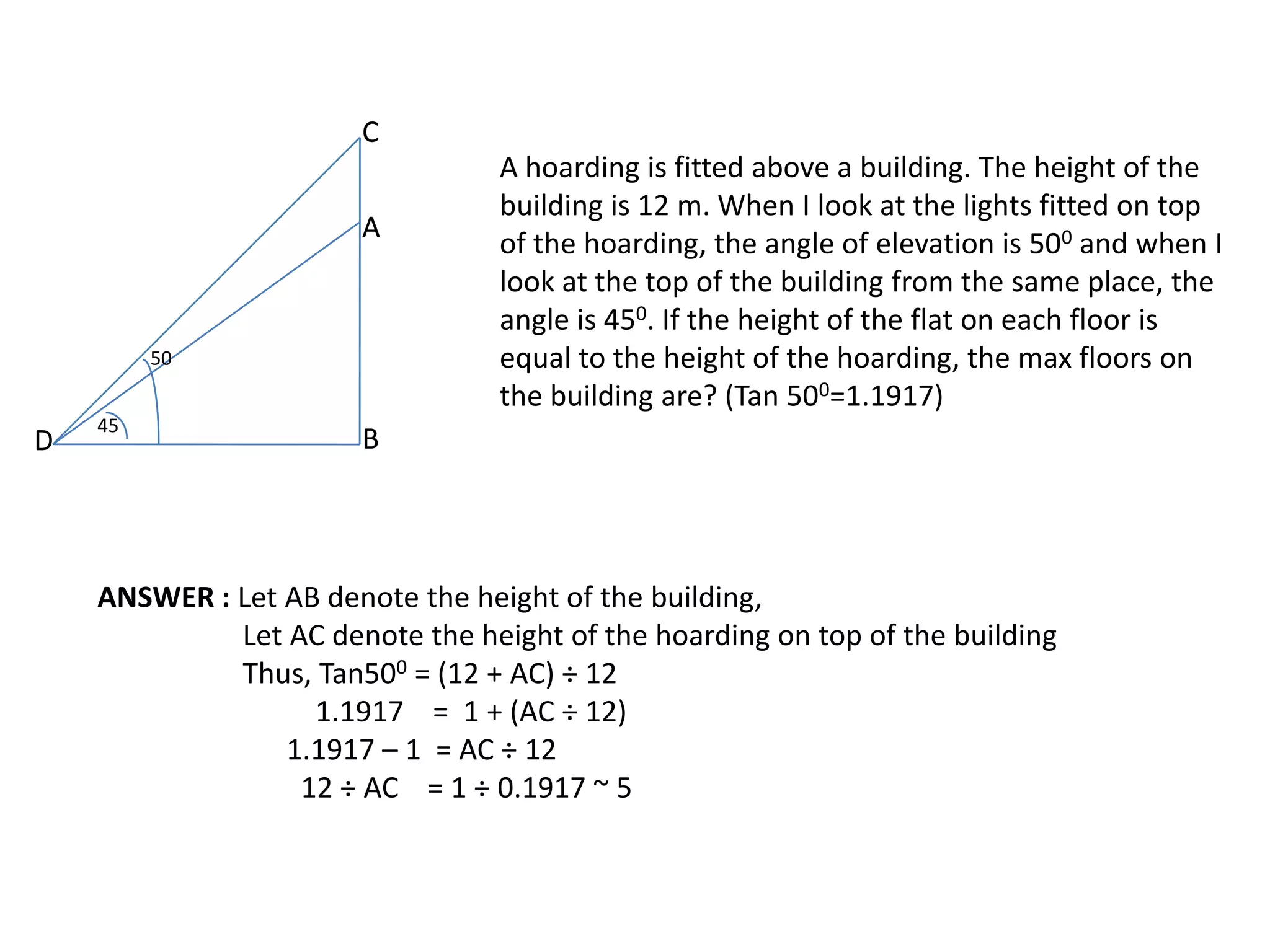
Trigonometry studies triangles and relationships between sides and angles. This document discusses using trigonometric ratios to calculate heights and distances, including the angles of elevation and depression. It provides examples of using trigonometry to find the height of a tower from the angle of elevation measured 30 meters away (30 meters high), and the height of a pole from the angle made by a rope tied to its top (10 meters high). It also explains calculating the length of a kite string from the angle of elevation.

2. Some
Applications of
Trigonometry

3. What is Trigonometry?
Trigonometry is a branch
of mathematics that studies triangles and the
relationships between their sides and the angles
between these sides.

4. In this topic we shall make use of
Trigonometric Ratios to find the height of
a tree, a tower, a water tank, width of a
river, distance of ship from lighthouse etc.

5. Basic Fundamentals

6. Line of Sight
Horizontal

7. Angle of Elevation
The angle which the line of sight
makes with a horizontal line drawn
away from their eyes is called the
angle of Elevation of aero plane from
them.
Angel of Elevation

8. • Angle of Elevation: In the picture below, an
observer is standing at the top of a building is
looking straight ahead (horizontal line). The
observer must raise his eyes to see the airplane
(slanting line). This is known as the angle of
elevation.

9. • Angle of Depression: The angle below horizontal that an
observer must look to see an object that is lower than
the observer. Note: The angle of depression is congruent
to the angle of elevation (this assumes the object is close
enough to the observer so that the horizontals for the
observer and the object are effectively parallel).

10. Angle of Depression
Horizontal
Angel of Depression

11. Trigonometric Ratios

12. Now let us Solve some
problem related to
Height and Distance

13. The angle of elevation of the top of a tower from a
point on the ground, which is 30 m away from the
foot of the tower is 30°. Find the height of the tower.
.
Let AB be the tower and the angle of elevation from point C
(on ground) is
30°.
In ΔABC,
Therefore, the height of the tower is

14. A circus artist is climbing a 20 m long rope, which is tightly
stretched and tied from the top of a vertical pole to the
ground. Find the height of the pole, if the angle made by the
rope with the ground level is 30 °.
Sol:- It can be observed from the figure that AB is the pole.
In ΔABC,
Therefore, the height of the pole is 10 m.

15. .
Let K be the kite and the string is tied to point P on
the ground.
In ΔKLP,
Hence, the length of the string is

16. ,

17. .
Height of tree =
+ BC
Hence, the height of the tree is

20. 1
Tan 30
h
3
Tan 60
h
3
d
From (1) d
(1)
d
The angle of elevation of the top of a tower from a
point At the foot of the tower is 300 . And after
advancing 150mtrs Towards the foot of the tower, the
angle of elevation becomes 600 .Find the height of
the tower
(2)
150
h 3
From ( 2 )
3 (d
h
150 )
h
30
60
Substituti ng ..the ..value ..of .. d ..
3 (h 3
3h
150
3h
h
2h
150
h
150 )
3
h
150
h
3
d
3
75 * 1 . 732
150
129 . 9 m

21. Questions based on trigonometry :• The angle of elevation of the top of a pole measures 48° from a point on
the ground 18 ft. away from its base. Find the height of the flagpole.
• Solution
Step 1: Let’s first visualize the situation
Step 2: Let ‘x’ be the height of the flagpole.
STEP 3: From triangle ABC,tan48=x/18
Step 4: x = 18 × tan 48° = 18 × 1.11061… = 19.99102…» 20
Step 5: So, the flagpole is about 20 ft. high.

22. C
A
50
D
45
A hoarding is fitted above a building. The height of the
building is 12 m. When I look at the lights fitted on top
of the hoarding, the angle of elevation is 500 and when I
look at the top of the building from the same place, the
angle is 450. If the height of the flat on each floor is
equal to the height of the hoarding, the max floors on
the building are? (Tan 500=1.1917)
B
ANSWER : Let AB denote the height of the building,
Let AC denote the height of the hoarding on top of the building
Thus, Tan500 = (12 + AC) ÷ 12
1.1917 = 1 + (AC ÷ 12)
1.1917 – 1 = AC ÷ 12
12 ÷ AC = 1 ÷ 0.1917 ~ 5