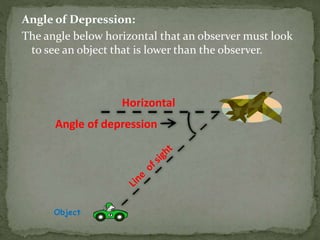
Trigonometry focuses on the properties and relationships of triangles, particularly right triangles, and has applications in various fields including astronomy, geography, and navigation. It involves trigonometric functions like sine, cosine, and tangent, which are ratios of triangle sides. The document provides examples of calculating heights and distances using these functions in real-life scenarios.

2. Trigonometry is the branch of mathematics that deals
with triangles particularly right triangles.
They are behind how sound and light move and are also
involved in our perceptions of beauty and other facets
on how our mind works.
So trigonometry turns out to be the fundamental to
pretty much everything!

3. A trigonometric function is a ratio of certain parts of a triangle. The
names of these ratios are: The sine, cosine, tangent, cosecant, secant,
cotangent.
Let us look at this triangle…
a
c
b
ө
A
B
C
Given the assigned letters to the sides
and angles, we can determine the
following trigonometric functions.
Sinθ=
Cos θ=
Tan θ=
Side Opposite
Hypotenuse
Side Adjacent
Hypotenuse
Side Opposite
Side Adjacent
=
=
a
c
b
c
= a
b

4. 1
1
1
1
1

45
2
45
2
45

 
Sin
Cos
Tan
3
1
3

30
2
30
1
2
30


Sin
Cos
Tan
3
3
1
1

60
2
60
2
60


Sin
Cos
Tan
0
0
 
1
 
0
1
0
1
1
0
0
1
0
 
Sin
Cos
Tan
Sin
Cos
1
 
0
1

Tan n .
d
0
90
1
90
1
1
90
 

5. One of the most ancient subjects studied
by scholars all over the world, astronomers have
used trigonometry to calculate the distance
from the earth to the planets and stars.
Its also used in geography and in
navigation.
The knowledge of trigonometry is used
to construct maps, determine the
position of an island in
relation to longitudes and latitudes.
Trigonometry is used in almost every
sphere of life around you.
Angle of
depression
Angle of
elevation

6. Angle of Elevation: In the picture below, an observer
is standing at the top of a building is looking straight
ahead (horizontal line). The observer must raise his
eyes to see the airplane (slanting line). This is known
as the angle of elevation.
Angle of elevation
Horizontal

7. Angle of Depression:
The angle below horizontal that an observer must look
to see an object that is lower than the observer.
Horizontal
Angle of depression
Object

8. The angle of elevation of the top of a pole measures 45° from a
point on the ground 18 ft. away from its base. Find the height
of the flagpole.
Solution
Let’s first visualize the situation
Let ‘x’ be the height of the flagpole.
From triangle ABC, tan 45 ° =x/18
x = 18 × tan 45° = 18 × 1=18ft
So, the flagpole
is 18 ft. high.
45 °

9. A tower stands on the ground. The angle of elevation
from a point on the ground which is 30 metres away from the foot
Of the tower is 30⁰. Find the height of the tower. (Take √3 = 1.732)
Let AB be the tower h metre high.
Let C be a point on the ground
which is 30 m away from point B,
the foot of the tower.
30⁰
So BC = 30 m
Then ACB = 30⁰
Now we have to find AB i.e. height ‘h’
of the tower .
30 m
h
A
B
C
Solution .

10. Now we shall find the trigonometric ratio combining
AB and BC .
AB
B
tan 30⁰
1
√3
h
30
h 30
√3
30 x √3
√3 x √3
30 x √3
3
10√3 m
10 x 1.732 m
17.32 m
Hence, height of the tower = 17.32 m
30⁰
30 m
h
A
B
C

11. An airplane is flying at a height of 2 miles above the level ground.
The angle of depression from the plane to the foot of a tree is 30°.
Find the distance that the air plane must fly to be directly above
the tree.
30 °
30 °
Step 1: Let ‘x’ be the distance the airplane
must fly to be directly above the tree.
Step 2: The level ground and
the horizontal are parallel, so
the alternate interior angles are equal in
measure.
Step 3: In triangle ABC, tan 30=AB/x.
Step 4: x = 2 / tan 30
Step 5: x = (2*31/2)
Step 6: x = 3.464
So, the airplane must fly about 3.464
miles to be directly above the tree.
D