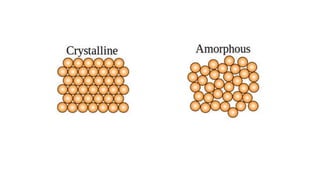
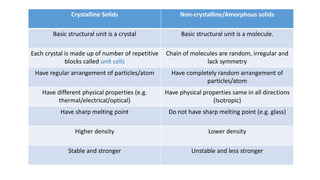
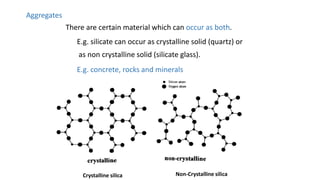
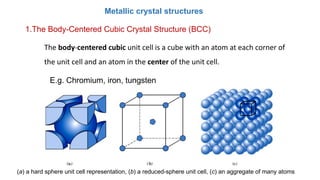
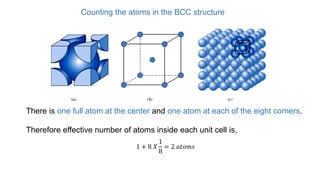
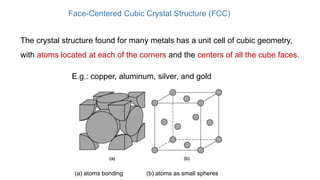
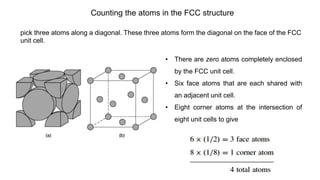
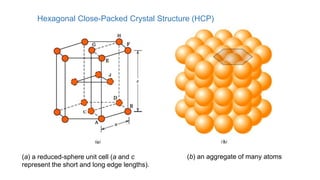
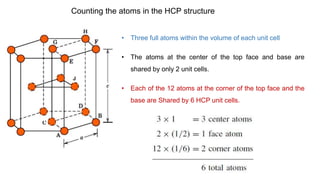
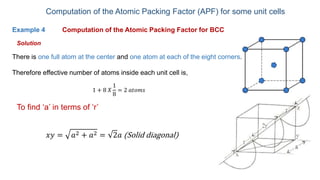
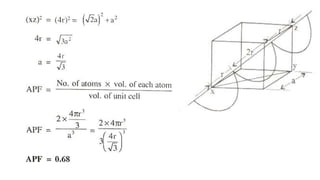
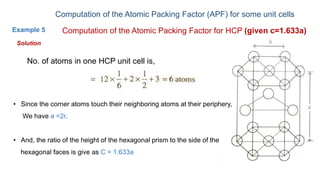
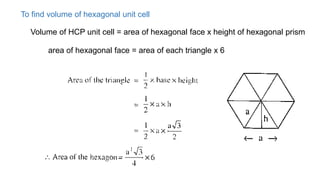
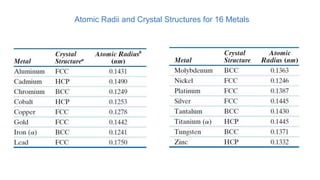
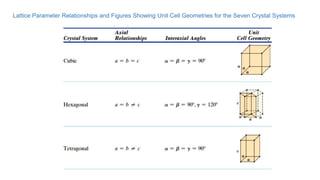
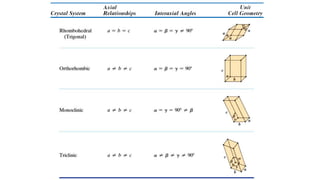
The document introduces the fundamentals of materials science and engineering, focusing on crystal structures such as body-centered cubic (bcc), face-centered cubic (fcc), and hexagonal close-packed (hcp) configurations. It explains the characteristics of crystalline vs. non-crystalline materials, emphasizing differences in atomic arrangement and physical properties. Additionally, it covers atomic packing factors, diffusion laws, and provides examples of various crystalline materials.

1. Introduction to Materials Science
and Engineering
Department of IE & M
JSS Academy of Technical Education, Bangalore-560060

2. UNIT - 1
Crystal Structure: BCC, FCC and HCP Structures, coordination number and
atomic packing factors, crystal imperfections -point line and surface
imperfections. Atomic Diffusion: Phenomenon, Fick’s laws of diffusion, factors
affecting diffusion
The Structure of Crystalline Solids

3. WHY STUDY The Structure of Crystalline Solids?
Significant property differences exist between crystalline and non-crystalline
materials having the same composition.
Example: Noncrystalline ceramics and polymers normally are optically
transparent; the same materials in crystalline (or semi crystalline) form tend
to be opaque or, at best, translucent.

4. Crystal Structures
Fundamental concepts
Solid materials may be classified according to the regularity with which atoms
or ions are arranged with respect to one another.
 crystalline solids / material
 Non Crystalline material / amorphous solids

5. A crystalline material is one in which the atoms are situated in a repeating
or periodic array over large atomic distances; such that upon solidification,
the atoms will position themselves in a repetitive three-dimensional pattern,
in which each atom is bonded to its nearest-neighbor atoms.
Crystalline solids / material
All metals, many ceramic materials, and certain polymers form crystalline
structures

7. Crystalline Solids Non-crystalline/Amorphous solids
Basic structural unit is a crystal Basic structural unit is a molecule.
Each crystal is made up of number of repetitive
blocks called unit cells
Chain of molecules are random, irregular and
lack symmetry
Have regular arrangement of particles/atom Have completely random arrangement of
particles/atom
Have different physical properties (e.g.
thermal/electrical/optical)
Have physical properties same in all directions
(Isotropic)
Have sharp melting point Do not have sharp melting point (e.g. glass)
Higher density Lower density
Stable and stronger Unstable and less stronger

8. Aggregates
There are certain material which can occur as both.
E.g. silicate can occur as crystalline solid (quartz) or
as non crystalline solid (silicate glass).
E.g. concrete, rocks and minerals
Crystalline silica Non-Crystalline silica

9. Unit cells
Unit cell is the basic structural unit or building block of the crystal structure
and defines the crystal structure by virtue of its geometry and the atom
positions within.

10. Three relatively simple crystal structures are found for most of the common
metals:
 face-centered cubic (FCC)
 body-centered cubic (BCC)
 hexagonal close-packed (HCP)
Metallic crystal structures

11. Metallic crystal structures
1.The Body-Centered Cubic Crystal Structure (BCC)
The body-centered cubic unit cell is a cube with an atom at each corner of
the unit cell and an atom in the center of the unit cell.
(a) a hard sphere unit cell representation, (b) a reduced-sphere unit cell, (c) an aggregate of many atoms
E.g. Chromium, iron, tungsten

12. There is one full atom at the center and one atom at each of the eight corners.
Therefore effective number of atoms inside each unit cell is,
1 + 8 𝑋
1
8
= 2 𝑎𝑡𝑜𝑚𝑠
Counting the atoms in the BCC structure

13. Face-Centered Cubic Crystal Structure (FCC)
The crystal structure found for many metals has a unit cell of cubic geometry,
with atoms located at each of the corners and the centers of all the cube faces.
E.g.: copper, aluminum, silver, and gold
(a) atoms bonding (b) atoms as small spheres

14. Counting the atoms in the FCC structure
pick three atoms along a diagonal. These three atoms form the diagonal on the face of the FCC
unit cell.
• There are zero atoms completely enclosed
by the FCC unit cell.
• Six face atoms that are each shared with
an adjacent unit cell.
• Eight corner atoms at the intersection of
eight unit cells to give

15. Determination of FCC Unit Cell Volume
Calculate the volume of an FCC unit cell in terms of the atomic radius R.
• the atoms touch one another across a face-
diagonal the length of which is 4R.
• Since the unit cell is a cube, its volume is a3
Where ‘a’ cell edge length.
• From the right triangle on the face,
Example 1

16. Hexagonal Close-Packed Crystal Structure (HCP)
 The top and bottom faces of the unit cell consist of six atoms that
form regular hexagons and surround a single atom in the center.
 Another plane that provides three additional atoms to the unit
cell is situated between the top and bottom planes.
 The atoms in this mid plane have as nearest neighbors atoms in
both of the adjacent two planes.

17. (a) a reduced-sphere unit cell (a and c
represent the short and long edge lengths).
(b) an aggregate of many atoms
Hexagonal Close-Packed Crystal Structure (HCP)

18. Counting the atoms in the HCP structure
• Three full atoms within the volume of each unit cell
• The atoms at the center of the top face and base are
shared by only 2 unit cells.
• Each of the 12 atoms at the corner of the top face and the
base are Shared by 6 HCP unit cells.

19. • coordination number
• APF (Atomic Packing Factor)
Characteristics of a crystal structure
Each atom has the same number of nearest-neighbor atoms, which is the
coordination number
 For face-centered cubics, the coordination number is 12
• Front face atom has four corner nearest-neighbor atoms surrounding it.
• Four face atoms that are in contact from behind.
• Four other equivalent face atoms residing in the next unit cell to the front,
which is not shown.

20. Atomic packing factor (APF)
The APF is the sum of the sphere volumes of all atoms within a unit cell divided by
the unit cell volume. —that is,
FCC structure, the atomic packing factor is 0.74

21. Computation of the Atomic Packing Factor for FCC
Show that the atomic packing factor for the FCC crystal structure is 0.74
Solution
Example 2
The total atom and unit cell volumes may be calculated in terms of the atomic radius R.
The volume for a sphere is -
since there are 4 atoms per FCC unit cell, the total FCC atom (or sphere) volume is,

22. From Example1, the total unit cell volume is
Therefore, the atomic packing factor is

23. Computation of the Atomic Packing Factor (APF) for some unit cells
Computation of the Atomic Packing Factor for SC (Simple cubic)Example 3
Let a = lattice constant
r = atomic radius
The center of each atom coincides with the different corners of the
cube and the atoms touch each other at their periphery.
Let us take a =2r
Each one of the atoms at the corners of the cube has effectively only 1/8th of its volume
present inside the cubic cell,
a
8 𝑋
1
8
= 1 𝑎𝑡𝑜𝑚𝑠

24. APF = 0.52

25. Computation of the Atomic Packing Factor (APF) for some unit cells
Example 4 Computation of the Atomic Packing Factor for BCC
There is one full atom at the center and one atom at each of the eight corners.
Therefore effective number of atoms inside each unit cell is,
1 + 8 𝑋
1
8
= 2 𝑎𝑡𝑜𝑚𝑠
Solution
To find ‘a’ in terms of ‘r’
𝑥𝑦 = 𝑎2 + 𝑎2 = 2𝑎 (Solid diagonal)

27. Computation of the Atomic Packing Factor (APF) for some unit cells
Example 5 Computation of the Atomic Packing Factor for HCP (given c=1.633a)
No. of atoms in one HCP unit cell is,
Solution
• Since the corner atoms touch their neighboring atoms at their periphery,
We have a =2r.
• And, the ratio of the height of the hexagonal prism to the side of the
hexagonal faces is give as C = 1.633a

28. To find volume of hexagonal unit cell
Volume of HCP unit cell = area of hexagonal face x height of hexagonal prism
area of hexagonal face = area of each triangle x 6

30. List of Formulae

32. Atomic Radii and Crystal Structures for 16 Metals

33. Lattice Parameter Relationships and Figures Showing Unit Cell Geometries for the Seven Crystal Systems

35. End of Module 2