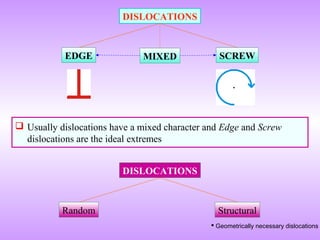
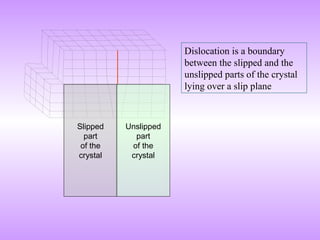
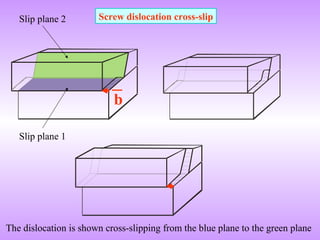
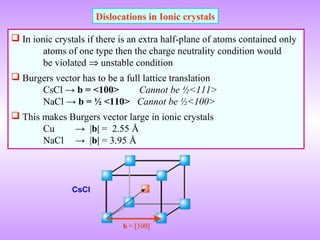
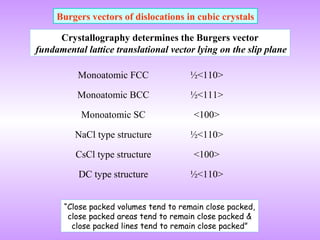
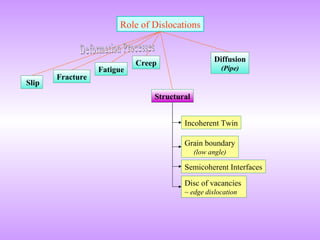
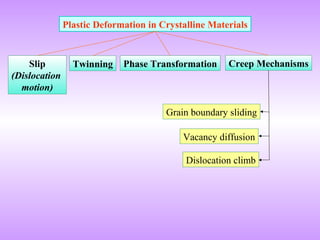
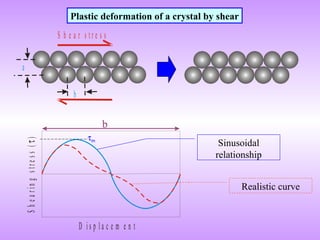
 Dislocations are line defects in crystals that represent disrupted planes of atoms. They allow plastic deformation via slip along crystallographic planes and directions.  A dislocation is characterized by its Burgers vector, which represents the lattice displacement caused by the dislocation and determines the direction of slip. The Burgers vector connects one lattice position to another.  Dislocations lower the theoretical shear strength of crystals by several orders of magnitude, enabling plasticity. Their motion through glide and climb allows crystals to deform plastically under stress.

1. DDIISSLLOOCCAATTIIOONNSS
 Edge dislocation
 Screw dislocation

2. Slip
(Dislocation
motion)
Plastic Deformation in Crystalline Materials
Twinning Phase Transformation Creep Mechanisms
Grain boundary sliding
Vacancy diffusion
Dislocation climb

3. Plastic deformation of a crystal by shear
S h e a r i n g s t r e s s ( t )
S h e a r s t r e s s
D i s p l a c e m e n t
Sinusoidal
relationship
Realistic curve
a
b
tm

4. Sin x m
As a first approximation the t t 2p
ö çè
÷ø
= æ
b
stress-displacement curve can be
written as
At small values of displacement t = Gg = G x
Hooke’s law should apply
a
t t 2p
ö çè
÷ø
= æ
b
x
m
Þ For small values of x/b
G b
a
t
m p
2
Hence the maximum shear =
stress at which slip should occur
t G
2 m
p
If b ~ a :

5.  The shear modulus of metals is in the range 20 – 150 GPa
t G
2 m
p
:
 The theoretical shear stress will be
in the range 3 – 30 GPa
 Actual shear stress is 0.5 – 10 MPa
 I.e. (Shear stress)theoretical > 100 * (Shear stress)experimental !!!!
DISLOCATIONS
Dislocations weaken the crystal

6. Carpet Pull

7. EDGE
DISLOCATIONS
MIXED SCREW
 Usually dislocations have a mixed character and Edge and Screw
dislocations are the ideal extremes
Random
DISLOCATIONS
Structural
 Geometrically necessary dislocations

8. Slipped
part
of the
crystal
Unslipped
part
of the
crystal
Dislocation is a boundary
between the slipped and the
unslipped parts of the crystal
lying over a slip plane

9. A dislocation has associated with it two vectors:

t ® A unit tangent vector along the dislocation line

b® The Burgers vector

10. Burgers Vector
Perfect crystal
Edge dislocation
Crystal with edge dislocation
RHFS:
Right Hand Finish to Start
convention

11. Edge dislocation
t 
Direction of `t vector
dislocation line vector
b 
Direction of `b vector

12.  Dislocation is a boundary between the slipped and the unslipped parts
of the crystal lying over a slip plane
 The intersection of the extra half-plane of atoms with the slip plane
defines the dislocation line (for an edge dislocation)
 Direction and magnitude of slip is characterized by the Burgers vector
of the dislocation
(A dislocation is born with a Burgers vector and expresses it even in
its death!)
 The Burgers vector is determined by the Burgers Circuit
 Right hand screw (finish to start) convention is used for determining
the direction of the Burgers vector
 As the periodic force field of a crystal requires that atoms must move
from one equilibrium position to another Þ b must connect one
lattice position to another (for a full dislocation)
 Dislocations tend to have as small a Burgers vector as possible

13.  The edge dislocation has compressive stress field above and tensile
stress field below the slip plane
 Dislocations are non-equilibrium defects and would leave the crystal
if given an opportunity

14. Compressive stress
field
Tensile stress
field

15. O STRESS FIELD OFF AA EEDDGGEE DDIISSLLOOCCAATTIIOONN
sX – FEM SIMULATED CONTOURS
(MPa)
FILM
27 Å 28 Å
SUBSTRATE
b
(x & y original grid size = b/2 = 1.92 Å)

16. Positive edge dislocation
Negative edge dislocation
ATTRACTION
REPULSION
Can come together and cancel
one another

17. Motion of
Edge
dislocation
Conservative
(Glide)
Non-conservative
(Climb)
Motion of dislocations
On the slip plane
Motion of dislocation
^ to the slip plane
 For edge dislocation: as b ^ t → they define a plane → the slip plane
 Climb involves addition or subtraction of a row of atoms below the
half plane
► +ve climb = climb up → removal of a plane of atoms
► -ve climb = climb down → addition of a plane of atoms

18. Edge Dislocation Glide
Shear stress
Surface
step

19. Edge Climb
Positive climb
Removal of a row of atoms
Negative climb
Addition of a row of atoms

20. Screw dislocation
[1]
[1] Bryan Baker
chemed.chem.purdue.edu/genchem/ topicreview/bp/materials/defects3.html -

21. Screw dislocation cross-slip
Slip plane 2
Slip plane 1
`b
The dislocation is shown cross-slipping from the blue plane to the green plane

22. The dislocation line ends on:
· The free surface of the crystal
· Internal surface or interface
· Closes on itself to form a loop
· Ends in a node
 A node is the intersection point of more than two dislocations
 The vectoral sum of the Burgers vectors of dislocations meeting at a
node = 0

23. Geometric properties of dislocations
Dislocation Property
Type of dislocation
Edge Screw
Relation between dislocation
line (t) and b ^ ||
Slip direction || to b || to b
Direction of dislocation line
movement relative to b || ^
Process by which dislocation
may leave slip plane climb Cross-slip

24. Mixed dislocations
`b `t
`b
Pure screw Pure Edge

25. Motion of a mixed dislocation
[1] http://www.tf.uni-kiel.de/matwis/amat/def_en/kap_5/backbone/r5_1_2.html
[1]
We are looking at the plane of the cut (sort of a semicircle centered in the lower left corner). Blue circles denote
atoms just below, red circles atoms just above the cut. Up on the right the dislocation is a pure edge dislocation
on the lower left it is pure screw. In between it is mixed. In the link this dislocation is shown moving in an
animated illustration.

26. Energy of dislocations
 Dislocations have distortion energy associated with them
 E per unit length
 Edge → Compressive and tensile stress fields
Screw → Shear strains
Energy of dislocation
Elastic
Non-elastic (Core)
E
~E/10
2
E @ 1 Gb Energy of a dislocation / unit length
2
G → (m) shear modulus
b → |b|

27. E @ 1 Gb 2
Þ Dislocations will have as small a b as possible
2
Dislocations
(in terms of lattice translation)
Full
Partial
b → Full lattice translation
b → Fraction of lattice
translation

28. Dissociation of dislocations
Consider the reaction:
2b → b + b
Change in energy:
G(2b)2/2 → 2[G(b)2/2]
G(b)2
Þ The reaction would be favorable

29. 2
1 211
6
b = éë ùû
3
1 12 1
6
b = éë ùû
1
(111)
1 110
2
b = éë ùû
(111)
Slip plane
(111)
1 [110]
2
1 [121]
6
æ ö
çè ø¸ (111)
æ ö
çè ø¸ (111)
1 [211]
6
æ ö
çè ø¸ → +
b1
2 > (b2
2 + b3
2)
½ > ⅓
FCC
Shockley Partials
A
B
C
(111)
(111)
Some of the atoms are omitted for clarity
(111)
1 [12 1]
6
æ ö
çè ø¸
(111)
1 [211]
6
æ ö
çè ø¸

30. FCC Pure edge dislocation
Dislocation line vector
Slip plane
Extra half plane
Burger’s vector
The extra- “half plane” consists of two ‘planes’ of atoms

31. BCC Pure edge dislocation
Dislocation line vector
(110)
(110),(111)
1 [1 1 1]
2
æ ö
çè ø¸
1 [112]
2
æ ö
çè ø¸
(111)
(1 10)
Slip plane
Extra half plane
Burger’s vector
1 [111]
1 2 112
2
éë ùû
(110)

32. Dislocations in Ionic crystals
 In ionic crystals if there is an extra half-plane of atoms contained only
atoms of one type then the charge neutrality condition would
be violated Þ unstable condition
 Burgers vector has to be a full lattice translation
CsCl → b = <100> Cannot be ½<111>
NaCl → b = ½ <110> Cannot be ½<100>
 This makes Burgers vector large in ionic crystals
Cu → |b| = 2.55 Å
NaCl → |b| = 3.95 Å
CsCl

33. Formation of dislocations (in the bulk of the crystal)
 Due to accidents in crystal growth from the melt
 Mechanical deformation of the crystal
 Annealed crystal: dislocation density (r) ~ 108 – 1010 /m2
 Cold worked crystal: r ~ 1012 – 1014 /m2

34. Burgers vectors of dislocations in cubic crystals
Crystallography determines the Burgers vector
fundamental lattice translational vector lying on the slip plane
Monoatomic FCC ½<110>
Monoatomic BCC ½<111>
Monoatomic SC <100>
NaCl type structure ½<110>
CsCl type structure <100>
DC type structure ½<110>
“Close packed volumes tend to remain close packed,
close packed areas tend to remain close packed &
close packed lines tend to remain close packed”

35. Slip systems
Crystal Slip plane(s) Slip direction
FCC {111} <110>
HCP (0001) <11`20>
BCC
Not close packed {110}, {112}, {123} [111]
No clear choice
Þ Wavy slip lines
Anisotropic

36. Slip
Role of Dislocations
Fracture
Fatigue
Creep Diffusion
(Pipe)
Structural
Incoherent Twin
Grain boundary
(low angle)
Semicoherent Interfaces
Disc of vacancies
~ edge dislocation