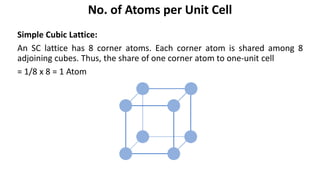
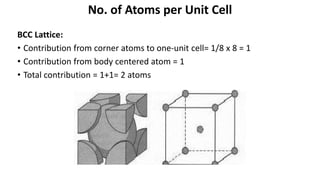
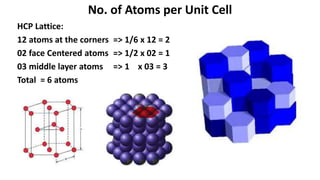
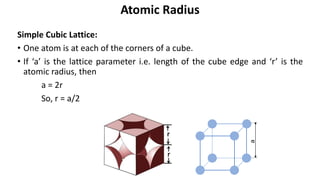
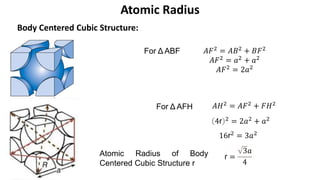
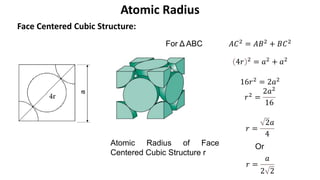
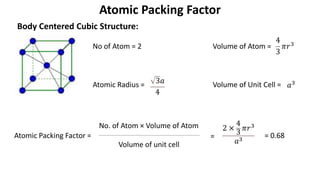
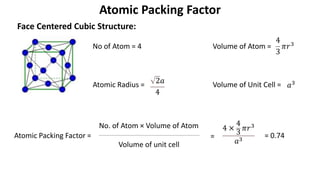
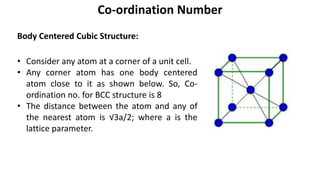
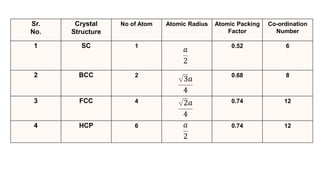
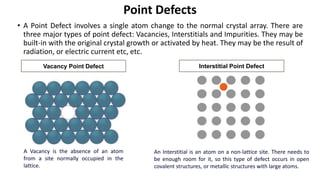
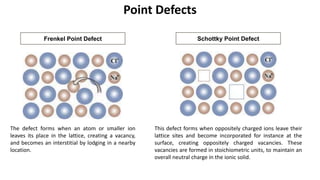
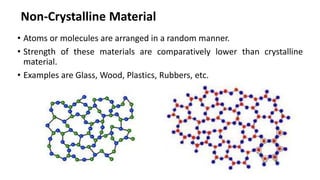
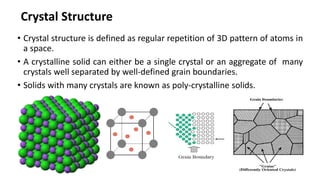
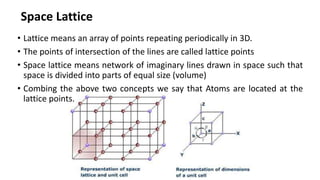
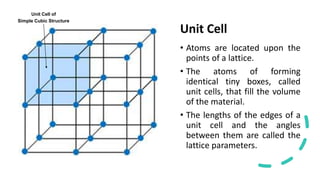
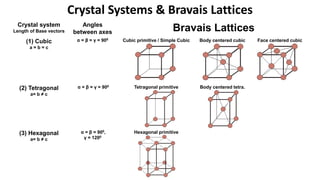
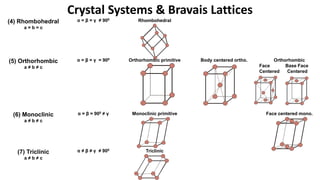
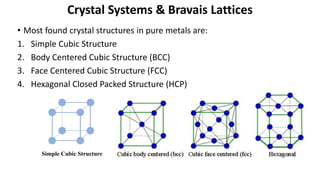
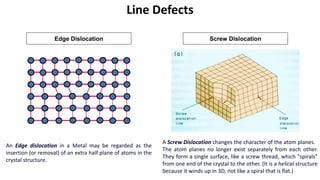
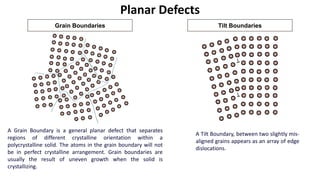
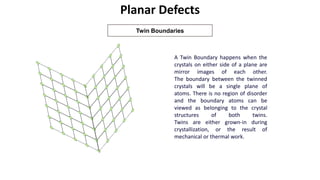
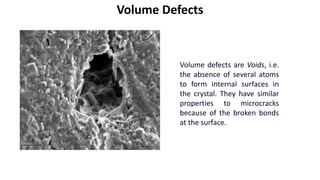
The document summarizes key concepts related to crystal structure: Crystalline materials have atoms or molecules arranged in a regular, orderly 3D pattern which gives them high strength, while non-crystalline materials have a random arrangement and lower strength. A crystal structure is a regular repetition of this 3D pattern defined by a unit cell and space lattice. Common crystal structures include simple cubic, body-centered cubic, face-centered cubic, and hexagonal close-packed. Crystal defects such as point defects, dislocations, grain boundaries, and voids are also discussed.

1. Crystal
Structure
By Ratnadeepsinh Jadeja

2. Crystalline Material
• Atoms or molecules are arranged in a very regular and orderly fashion in
3D pattern.
• Strength of these materials are comparatively high.
• Examples are Metals and Alloys.

3. Non-Crystalline Material
• Atoms or molecules are arranged in a random manner.
• Strength of these materials are comparatively lower than crystalline
material.
• Examples are Glass, Wood, Plastics, Rubbers, etc.

4. Crystal Structure
• Crystal structure is defined as regular repetition of 3D pattern of atoms in
a space.
• A crystalline solid can either be a single crystal or an aggregate of many
crystals well separated by well-defined grain boundaries.
• Solids with many crystals are known as poly-crystalline solids.

5. Space Lattice
• Lattice means an array of points repeating periodically in 3D.
• The points of intersection of the lines are called lattice points
• Space lattice means network of imaginary lines drawn in space such that
space is divided into parts of equal size (volume)
• Combing the above two concepts we say that Atoms are located at the
lattice points.

6. Unit Cell
• Atoms are located upon the
points of a lattice.
• The atoms of forming
identical tiny boxes, called
unit cells, that fill the volume
of the material.
• The lengths of the edges of a
unit cell and the angles
between them are called the
lattice parameters.
Unit Cell of
Simple Cubic Structure

7. Crystal Systems & Bravais Lattices
• The crystals are divided into 7 systems based on
1. Axial lengths
2. Interfacial angles
3. Directions of axis of symmetry
• There are 14 possible ways of arranging points in space lattice so that all
the lattice points have exactly same surroundings.

8. Crystal Systems & Bravais Lattices
Crystal system
Length of Base vectors
Angles
between axes Bravais Lattices
(1) Cubic
a = b = c
α = β = γ = 900 Cubic primitive / Simple Cubic Body centered cubic Face centered cubic
(2) Tetragonal
a= b ≠ c
α = β = γ = 900 Tetragonal primitive Body centered tetra.
(3) Hexagonal
a= b ≠ c
α = β = 900,
γ = 1200
Hexagonal primitive

9. Crystal Systems & Bravais Lattices
(4) Rhombohedral
a = b = c
α = β = γ ≠ 900 Rhombohedral
(5) Orthorhombic
a ≠ b ≠ c
α = β = γ = 900 Orthorhombic primitive Body centered ortho. Orthorhombic
Face Base Face
Centered Centered
(6) Monoclinic
a ≠ b ≠ c
α = β = 900 ≠ γ Monoclinic primitive Face centered mono.
(7) Triclinic
a ≠ b ≠ c
α ≠ β ≠ γ ≠ 900 Triclinic

10. • Most found crystal structures in pure metals are:
1. Simple Cubic Structure
2. Body Centered Cubic Structure (BCC)
3. Face Centered Cubic Structure (FCC)
4. Hexagonal Closed Packed Structure (HCP)
Simple Cubic Structure
Crystal Systems & Bravais Lattices

11. Simple Cubic Lattice:
An SC lattice has 8 corner atoms. Each corner atom is shared among 8
adjoining cubes. Thus, the share of one corner atom to one-unit cell
= 1/8 x 8 = 1 Atom
No. of Atoms per Unit Cell

12. BCC Lattice:
• Contribution from corner atoms to one-unit cell= 1/8 x 8 = 1
• Contribution from body centered atom = 1
• Total contribution = 1+1= 2 atoms
No. of Atoms per Unit Cell

13. FCC Lattice:
• In addition to eight corner atoms, there are six face centered atoms at six
planes of the cubes. Each of these six face centered atoms is equally
shared by two adjacent cubes. So,
• Contribution from corner atoms to one-unit cell= 1/8 x 8 = 1
• Contribution from face centered atoms to one-unit cell = 1/2 x 6 = 3
• Total = 1+3 = 4 atoms
No. of Atoms per Unit Cell

14. HCP Lattice:
12 atoms at the corners => 1/6 x 12 = 2
02 face Centered atoms => 1/2 x 02 = 1
03 middle layer atoms => 1 x 03 = 3
Total = 6 atoms
No. of Atoms per Unit Cell

15. It is possible to evaluate the radii of atoms by assuming that atoms are
spheres in contact with each other in a crystal. The atomic radius r is
defined as half the distance between the nearest neighbors in a crystal of a
pure element.
Atomic Radius

16. Simple Cubic Lattice:
• One atom is at each of the corners of a cube.
• If ‘a’ is the lattice parameter i.e. length of the cube edge and ‘r’ is the
atomic radius, then
a = 2r
So, r = a/2
Atomic Radius
a

17. Body Centered Cubic Structure:
Atomic Radius
𝐴𝐹2 = 𝐴𝐵2 + 𝐵𝐹2
𝐴𝐹2 = 𝑎2 + 𝑎2
𝐴𝐹2
= 2𝑎2
𝐴𝐻2 = 𝐴𝐹2 + 𝐹𝐻2
4r 2 = 2𝑎2 + 𝑎2
16r2 = 3𝑎2
r =
3𝑎
4
For Δ ABF
For Δ AFH
Atomic Radius of Body
Centered Cubic Structure r

18. Face Centered Cubic Structure:
Atomic Radius
a
For Δ ABC 𝐴𝐶2 = 𝐴𝐵2 + 𝐵𝐶2
4𝑟 2
= 𝑎2
+ 𝑎2
16𝑟2 = 2𝑎2
𝑟2 =
2𝑎2
16
𝑟 =
2𝑎
4
Atomic Radius of Face
Centered Cubic Structure r
𝑟 =
𝑎
2 2
Or

19. • In crystallography, atomic packing factor (APF) or packing fraction is the
fraction of volume in a crystal structure that is occupied by atoms.
• It is dimensionless and always less than unity.
• For practical purposes, the APF of a crystal structure is determined by
assuming that atoms are rigid spheres.
• The radius of the atoms (spheres) is taken to be the maximal value such
that the atoms do not overlap
• For one-component crystals (those that contain only one type of atom),
the APF is represented mathematically by
• Natoms is the number of atoms in the unit cell
• Vatom is the volume of an atom
• Vunit cell is the volume occupied by the unit cell.
Atomic Packing Factor

20. Simple Cubic Lattice:
Atomic Packing Factor
No of Atom in = 1
Atomic Radius = 𝑎
2
4
3
𝜋𝑟3
Volume of Atom =
Volume of unit cell = 𝑎3
Atomic Packing Factor =
No. of Atom × Volume of Atom
Volume of unit cell
1 ×
4
3 𝜋𝑟3
𝑎3= = 0.52

21. Body Centered Cubic Structure:
Atomic Packing Factor
No of Atom = 2 Volume of Atom =
Atomic Radius = Volume of Unit Cell =
Atomic Packing Factor =
No. of Atom × Volume of Atom
Volume of unit cell
2 ×
4
3 𝜋𝑟3
𝑎3= = 0.68
3𝑎
4
4
3
𝜋𝑟3
𝑎3

22. Face Centered Cubic Structure:
Atomic Packing Factor
No of Atom = 4 Volume of Atom =
Atomic Radius = Volume of Unit Cell =
Atomic Packing Factor =
No. of Atom × Volume of Atom
Volume of unit cell
4 ×
4
3 𝜋𝑟3
𝑎3= = 0.74
2𝑎
4
4
3
𝜋𝑟3
𝑎3

23. Hexagonal Cubic Structure:
Atomic Packing Factor
No of Atom = 6 Volume of Atom =
Atomic Radius = Volume of Unit Cell = 3 𝑎2
Sin 60 × c
Atomic Packing Factor =
No. of Atom × Volume of Atom
Volume of unit cell
6 ×
4
3 𝜋𝑟3
3 𝑎2 Sin 60 × c
= = 0.74
𝑎
2
4
3
𝜋𝑟3
Taking c/a ratio for HCP = 1.633

24. • Co-ordination Number defined as the number of nearest atoms directly
surrounding a given atom.
• It can also be defined as the nearest neighbors to an atom in a crystal.
• Remark : When co-ordination number is larger, the structure is more
closely packed.
Co-ordination Number

25. Simple Cubic Lattice:
Co-ordination Number
• Consider any atom at a corner of a unit
cell.
• Any corner atom has four nearest
neighbor atoms in the same plane and
two nearest neighbors in vertical plane
(one exactly above and the other
exactly below).
• So, Co-ordination no. for simple cubic
structure is 4+2 = 6
• The distance between the atom and any
of the nearest atom will be equal to
lattice parameter i.e. a.

26. Body Centered Cubic Structure:
Co-ordination Number
• Consider any atom at a corner of a unit cell.
• Any corner atom has one body centered
atom close to it as shown below. So, Co-
ordination no. for BCC structure is 8
• The distance between the atom and any of
the nearest atom is √3a/2; where a is the
lattice parameter.

27. Face Centered Cubic Structure:
Co-ordination Number
• Consider any atom at a corner of a unit cell.
• For any corner atom, there will be 4 face
centered atoms of the surrounding unit cells
in its own plane, 4 face centered atoms below
its plane and 4 face centered atoms above its
plane. So, Co-ordination no. for FCC structure
is 4+4+4 = 12
• The distance between the atom and any of
the nearest atom is a/√2; where a is the
lattice parameter.

28. Hexagonal Cubic Structure:
Co-ordination Number
• In HCP, each atom in one layer is
located directly above or below
interstices among three atoms in
the adjacent layers. So, each
atom touches three atoms in the
layer below its plane, six atoms
in its own plane, and three
atoms in the layer above. So, Co-
ordination no. for HCP structure
is 3+6+3 = 12

29. Sr.
No.
Crystal
Structure
No of Atom Atomic Radius Atomic Packing
Factor
Co-ordination
Number
1 SC 1 0.52 6
2 BCC 2 0.68 8
3 FCC 4 0.74 12
4 HCP 6 0.74 12
𝑎
2
3𝑎
4
𝑎
2
2𝑎
4

30. • A perfect crystal, with every atom of the same type in the correct
position, does not exist.
• All crystals have some defects. Defects contribute to the mechanical
properties of metals.
• Metals are not perfect neither at the macrolevel and nor at the microlevel
Crystal Defects

31. • There are basic classes of crystal defects:
1. Point defects, which are places where an atom is missing or irregularly
placed in the lattice structure. Point defects include lattice vacancies,
self-interstitial atoms, substitution impurity atoms, and interstitial
impurity atoms
2. Linear defects, which are groups of atoms in irregular positions. Linear
defects are commonly called dislocations.
3. Planar defects, which are interfaces between homogeneous regions of
the material. Planar defects include grain boundaries, stacking faults
and external surfaces.
4. Volume defects, the absence of several atoms to form internal surfaces
in the crystal. They have similar properties to microcracks because of
the broken bonds at the surface.
Crystal Defects

32. • A Point Defect involves a single atom change to the normal crystal array. There are
three major types of point defect: Vacancies, Interstitials and Impurities. They may be
built-in with the original crystal growth or activated by heat. They may be the result of
radiation, or electric current etc, etc.
Point Defects
A Vacancy is the absence of an atom
from a site normally occupied in the
lattice.
An Interstitial is an atom on a non-lattice site. There needs to
be enough room for it, so this type of defect occurs in open
covalent structures, or metallic structures with large atoms.
Vacancy Point Defect Interstitial Point Defect

33. Point Defects
The defect forms when an atom or smaller ion
leaves its place in the lattice, creating a vacancy,
and becomes an interstitial by lodging in a nearby
location.
Frenkel Point Defect
This defect forms when oppositely charged ions leave their
lattice sites and become incorporated for instance at the
surface, creating oppositely charged vacancies. These
vacancies are formed in stoichiometric units, to maintain an
overall neutral charge in the ionic solid.
Schottky Point Defect

34. Line Defects
Edge Dislocation Screw Dislocation
An Edge dislocation in a Metal may be regarded as the
insertion (or removal) of an extra half plane of atoms in the
crystal structure.
A Screw Dislocation changes the character of the atom planes.
The atom planes no longer exist separately from each other.
They form a single surface, like a screw thread, which "spirals"
from one end of the crystal to the other. (It is a helical structure
because it winds up in 3D, not like a spiral that is flat.)

35. Planar Defects
Grain Boundaries Tilt Boundaries
A Grain Boundary is a general planar defect that separates
regions of different crystalline orientation within a
polycrystalline solid. The atoms in the grain boundary will not
be in perfect crystalline arrangement. Grain boundaries are
usually the result of uneven growth when the solid is
crystallizing.
A Tilt Boundary, between two slightly mis-
aligned grains appears as an array of edge
dislocations.

36. Planar Defects
Twin Boundaries
A Twin Boundary happens when the
crystals on either side of a plane are
mirror images of each other.
The boundary between the twinned
crystals will be a single plane of
atoms. There is no region of disorder
and the boundary atoms can be
viewed as belonging to the crystal
structures of both twins.
Twins are either grown-in during
crystallization, or the result of
mechanical or thermal work.

37. Volume Defects
Volume defects are Voids, i.e.
the absence of several atoms
to form internal surfaces in
the crystal. They have similar
properties to microcracks
because of the broken bonds
at the surface.

38. Thank You