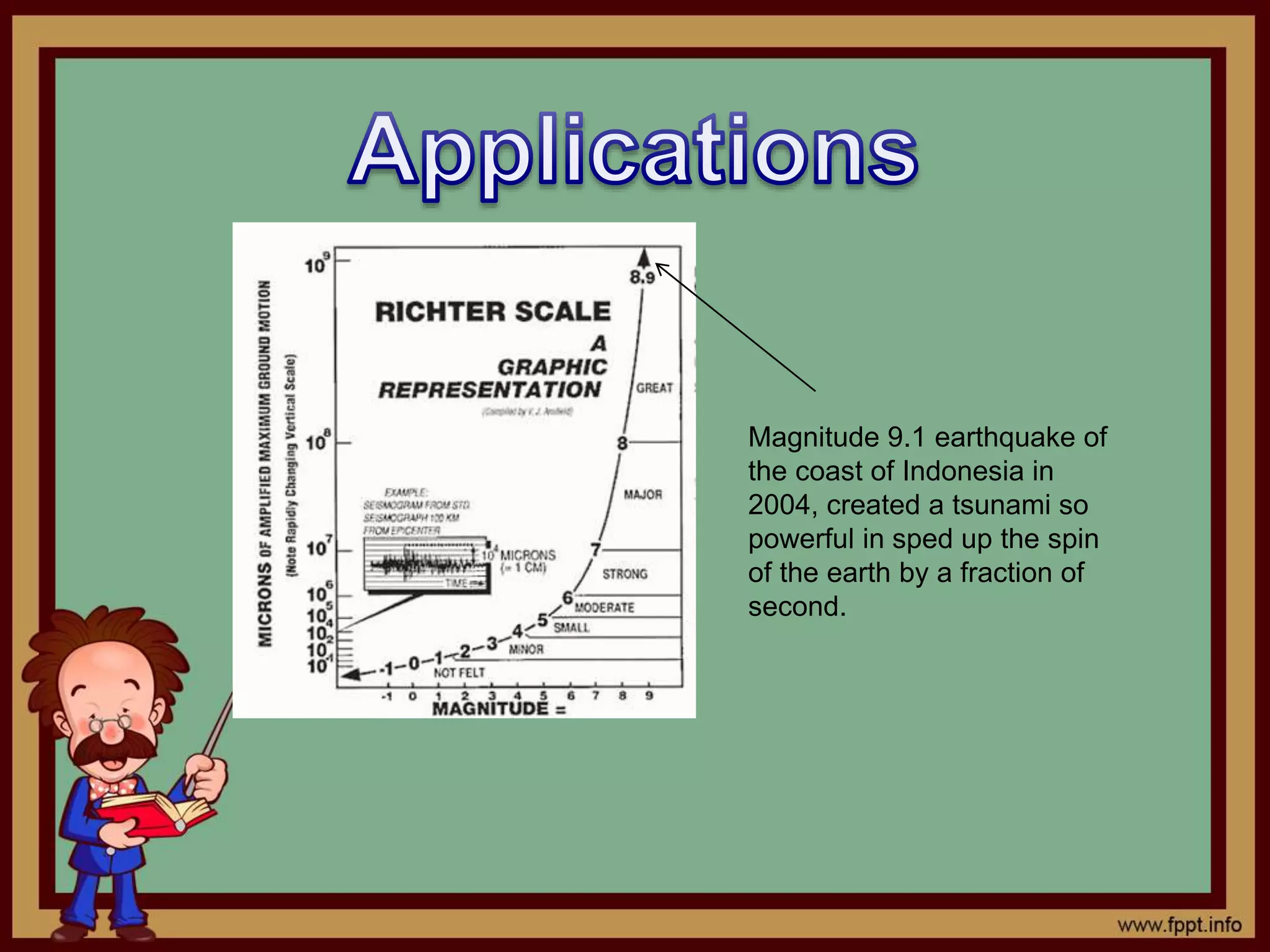
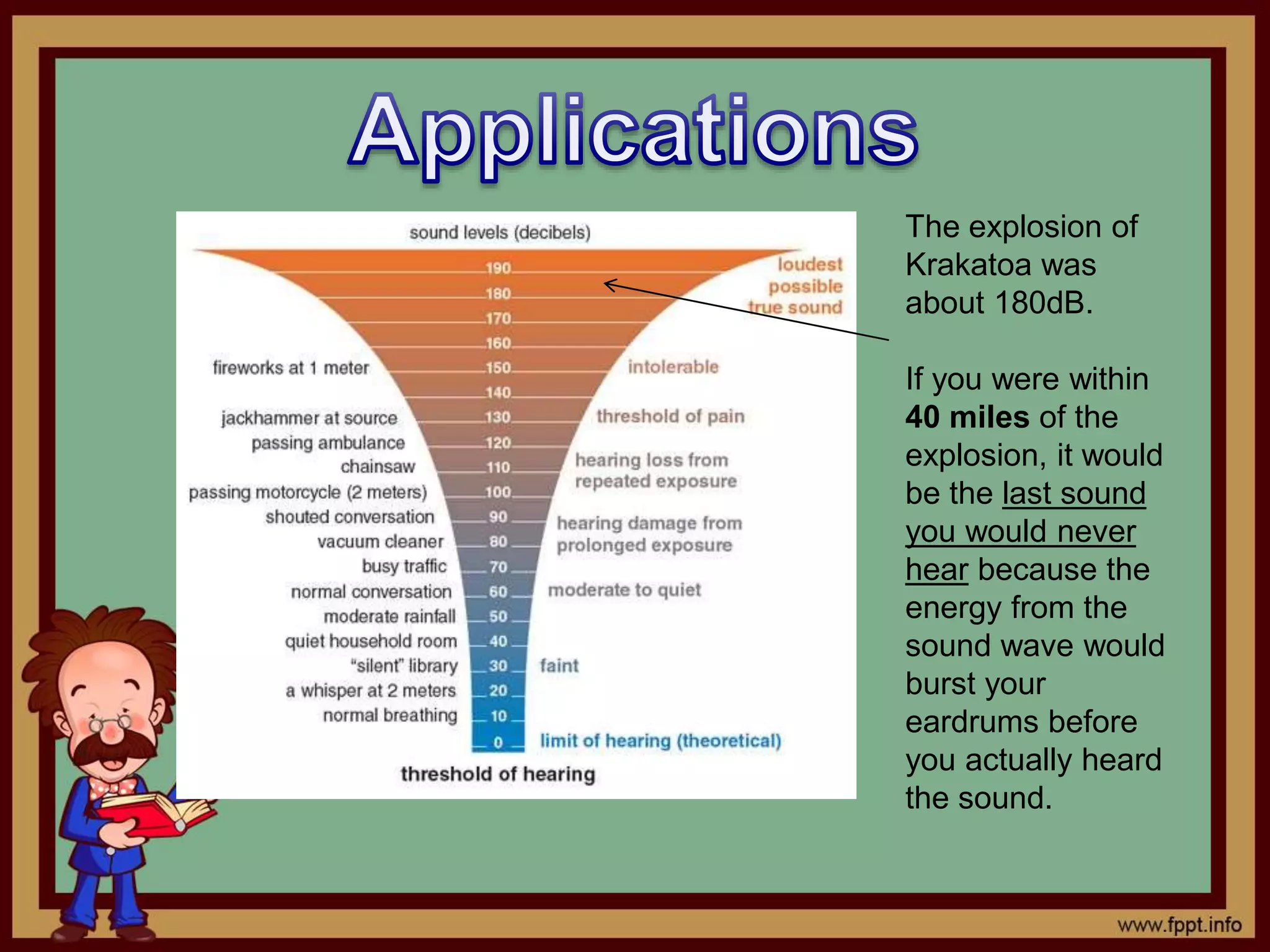
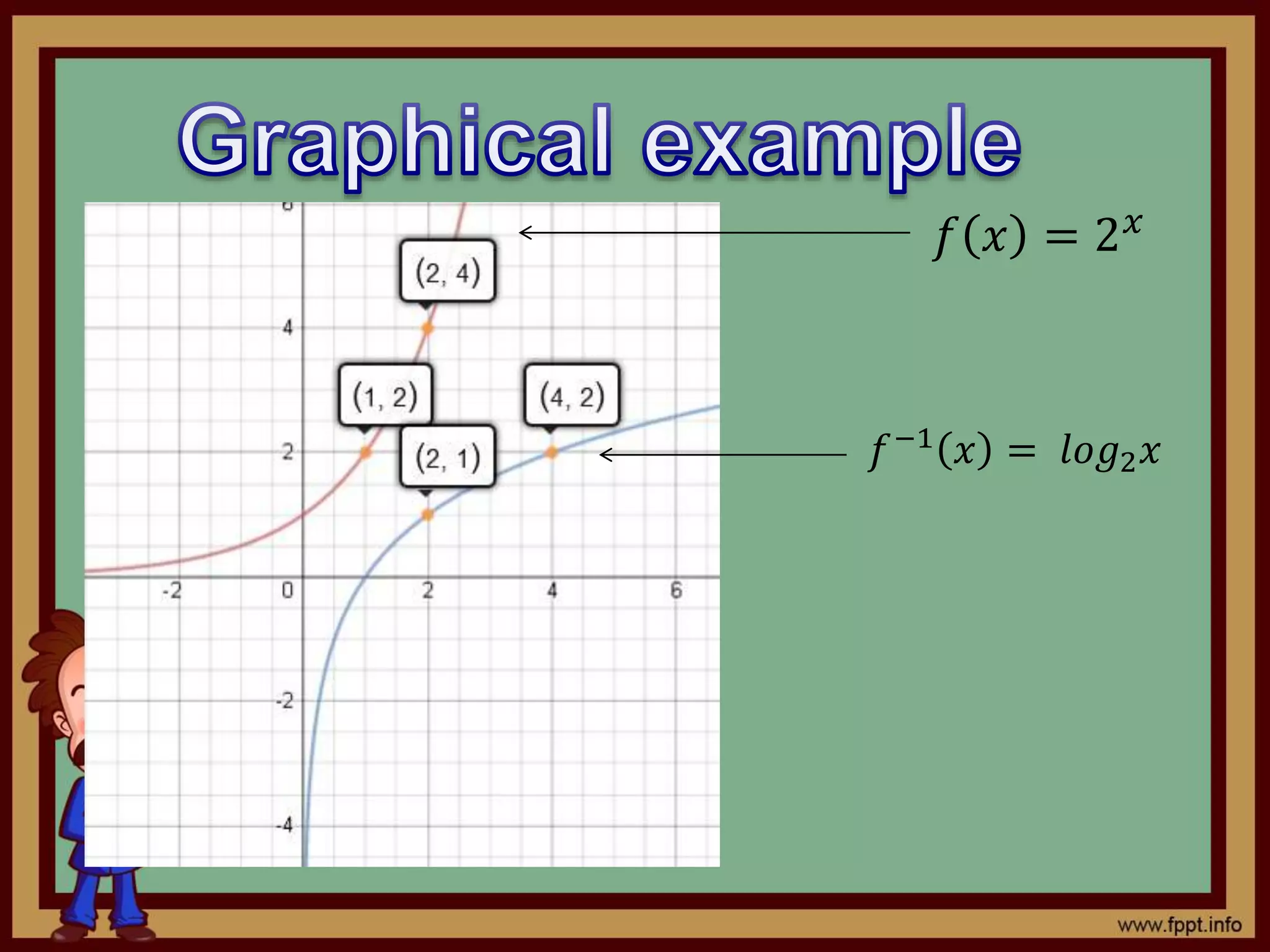
1) The document discusses logarithms and how they were developed to simplify calculations of large numbers before calculators. Logarithms allow expressing a number as an exponent by finding what power of a base number equals the target number. 2) It provides examples of converting between exponential and logarithmic forms, using logarithmic properties to solve equations, and using change of base formulas to solve when the calculator uses a different base than the problem. 3) Key steps are shown to solve the equation 5x = 15,000 by rewriting in logarithmic form, using the change of base formula to solve for x, and checking the exponential form of the answer.

1. Simplify-
1) 24
= 2) 1.53
= 3) 31.5
=
Solve for x (round to TWO decimal places if you have to)
4) 2 𝑥 = 8 5) 2 𝑥 = 20 6) 3 𝑥 = 100
How did you go about trying to find the answer
to #6 and #7?

2. Goals:
1) Explain the structure and the purpose of
logarithms
2) Solve equations using logarithms

3. …In the 11 or 12 years you were at school you
were taught the math that took over 6000 years to
develop.
The development of ‘x’
1) x+1 = 2 → adding/subtracting
2) 2x=4 → Multiplying/dividing
3) 𝑥2 = 4 → Powers/roots
4) 𝑥 = −1 → Imaginary/complex numbers
5) 2 𝑥
= 5 → exponents/logarithms

4. …Created logarithms to make
calculating big numbers easier
(before electronic calculators)
If you need to work with a big
messy number like:
123456789.97654321
You could instead say: For what
x will 10 𝑥equal the number I
want.
Since logs follow similar rules as
other operations it makes
calculating MUCH simpler.

5. Magnitude 9.1 earthquake of
the coast of Indonesia in
2004, created a tsunami so
powerful in sped up the spin
of the earth by a fraction of
second.

6. The explosion of
Krakatoa was
about 180dB.
If you were within
40 miles of the
explosion, it would
be the last sound
you would never
hear because the
energy from the
sound wave would
burst your
eardrums before
you actually heard
the sound.

7. Just like addition is the inverse of subtraction and multiplication is
the inverse of division,
Notes start here:
 Logarithms (or logs) are the inverse of exponents.
 If 𝑓 𝑥 = 2 𝑥, then logarithms answers the question
for what x will the following be true:
𝑥 = 2 𝑓 𝑥

8. 𝑓 𝑥 = 2 𝑥
𝑓−1 𝑥 = 𝑙𝑜𝑔2 𝑥

9. If 𝑏 𝑥
= 𝑎 then 𝑙𝑜𝑔 𝑏 𝑎 = 𝑥
as long as b > 1, b ≠ 0
Exponent base Log base

10. Write the following exponent equation in log form:
1) 52 = 25
2) 6 𝑥
= 100
3) Write your own

11. Write the following log equations in exponential form:
1) 𝑙𝑜𝑔232 = 8 2) 𝑙𝑜𝑔4 𝑥 = 20
3) 𝑙𝑜𝑔650 = 𝑥 4) Write your own

12. Rewrite in log form, use the change of base formula,
solve to THREE decimal places, check:
1) Rewrite in log form: 𝑙𝑜𝑔210 = 𝑥
2) Since most calculators are only able to do log base 10 and
log base e, you need to use a change of base formula:
𝑙𝑜𝑔 𝑥 𝑦 =
𝑙𝑜𝑔 𝑦
𝑙𝑜𝑔 𝑥
→ 𝑙𝑜𝑔210 =
𝑙𝑜𝑔10
𝑙𝑜𝑔2
3) Solve: x= 𝑙𝑜𝑔210 =
𝑙𝑜𝑔10
𝑙𝑜𝑔2
= 3.322
4) Check: 23.322
= 10 (close enough)

13. Solve and check: 5 𝑥 =
15,000
1) Log form → 𝑙𝑜𝑔____________ = x
2) Change of base and solve → 𝑙𝑜𝑔515000 =
𝑙𝑜𝑔____
𝑙𝑜𝑔____
= _______
3) Check you answer: 55.975
= 15008 (close enough but if I
needed to be more accurate I can always take more decimal
places.)