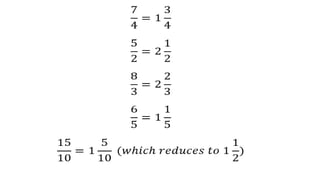The document defines rational numbers as numbers that can be expressed as a ratio of two integers. It describes the different types of rational numbers including natural numbers, whole numbers, integers, fractions (proper, improper, mixed), and decimals. It provides examples of each type. It also explains how to arrange rational numbers in ascending and descending order by expressing them with a common denominator and comparing numerators.

1. Rational
Numbers
 Identifying and Defining the types of
Rational Numbers
 Arranging Rational Numbers in
Ascending and Descending Order

2. Defining
Rational Numbers
In mathematics, a rational number is any number that can
be expressed as a ratio of two integers .For example, 1.5 is
rational since it can be written as 3/2, 6/4, 9/6 or another
fraction or two integers.
NB: Every integer is a rational number: for example, 5 = 5/1.

3. Types of Rational
Numbers
1. Natural numbers
2. Whole numbers
3. Integers
4. Fractions
-(Proper Fractions, Improper Fractions, Mixed Fractions)
5. Decimals

4. • Natural numbers -are numbers used for counting and ordering.
They are positive integers, beginning with 1. Therefore, some
examples include: 1, 2, 3, 4, 5 . . .
• Whole numbers- include all natural numbers with one big difference:
it also includes 0. So, when listing whole numbers, you could say 0, 1,
2, 3, 4 . . .
• Integers- include all natural and whole numbers. Integers apart from
the first two groups stated above is that they also include negative
numbers. Examples of integers include . . . -5, -4, -3, -2, -1, 0, 1, 2, 3,
4, 5 . . .

5. • Proper fractions- are numbers that are less than 1. Examples of fractions include
• If proper fractions are numbers less than 1 (a whole) therefore improper fractions are
numbers that are greater than 1. Maybe you have an entire pie plus an addition half of a pie
available. In this case, you could write the fraction as:
• When improper fractions are converted they become mixed fractions. Mixed fractions
include both proper fractions and whole numbers. If we look at the examples from the
improper fractions, we can turn the following improper fractions into mixed numbers:

7. Decimal numbers- also express values less than 1.
For example if a baby weighed 6.5 pounds at birth. The
decimal tells us that the baby weighed an extra half of a
pound. In between the numbers is a decimal point, which is
similar to a period. This tells us that all the numbers after the
decimal point are a percentage of the whole.

8. Arranging Rational
Numbers in ascending
order
• Step 1: Express the given rational number in terms of a positive
denominator.
• Step 2: Determine the Least Common Multiple of the positive
denominators obtained.
• Step 3: Express each rational number with the LCM acquired as the
common denominator.
• Step 4: The number which has the smaller numerator is the smaller

9. Example #1
Arrange the following rational numbers in Ascending Order -3/5,
-1/5, -2/5
Since all the numbers have a common denominator the one with a smaller
numerator is the smaller rational number. However, when it comes to
negative numbers the higher one is the smaller one.
Therefore arranging the given rational numbers we get -3/5, -2/5,
-1/5

10. Example #2
Arrange the rational numbers 1/2, -2/9, -4/3 in Ascending Order
Find the LCM of the denominators 2, 9, 3
LCM of 2, 9, 3 is 18
Express the given rational numbers with the LCM in terms of common denominator.
1/ 2= 1x9/2x9 = 9/18
-2/9 = -2x2/9x2 = -4/18
-4/3 = -4x6/3x6 = -24/18
Check the numerators of all the rational numbers expressed with a common denominator. Since -
24 is less than the other two we can arrange the given rational numbers in Ascending Order.
-4/3, -2/9, 1/2 is the Ascending Order of Given Rational Numbers.

11. Arranging Rational
Numbers in descending
order
• Step 1: Express the given rational numbers with positive
denominators.
• Step 2: Take the least common multiple (L.C.M.) of these positive
denominators.
• Step 3: Express each rational number (obtained in step 1) with this
least common multiple (LCM) as the common denominator
• Step 4:Compare the numerators and the highest numerator is the
largest one.

12. Example
Arrange the numbers 5/-3, 10/-7, -5/8 in Descending Order.
Express the Rational Numbers with Positive Denominators
5/-3 = 5*(-1)/-3*(-1) = -5/3
10/-7 = 10*(-1)/-7*(-1) = -10/7
-5/8 already has a positive denominator
Find the LCM of Positive Denominators. LCM of 3, 7, 8 is 168
Express the Rational Numbers with Common Denominator with the LCM obtained.
-5/3 = -5 x 56/3x56 = -280/ 168
-10/7 = -10x24/7x24 = -240/168
-5/8 = -5 x 21/8 x21 = -105/168
Check the numerators of the rational numbers. Since all of them are negative numbers