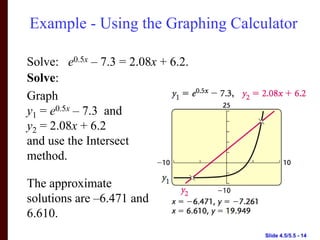
This document section discusses solving exponential and logarithmic equations. It provides examples of solving different types of exponential equations using properties of exponents and logarithms. It also gives examples of solving logarithmic equations by rewriting the equations in exponential form and then solving. The examples demonstrate solving equations with variables in exponents, logarithmic expressions with a single variable, and more complex equations involving logarithms of expressions. Graphing calculators can also be used to approximate solutions.

2. CHAPTER 4/5:
Exponential and
Logarithmic Functions
4.2/5.2 Exponential Functions and Graphs
4.3/5.3 Logarithmic Functions and Graphs
4.4/5.4 Properties of Logarithmic Functions
4.5/5.5 Solving Exponential and Logarithmic
Equations
4.6/5.6 Applications and Models: Growth and
Decay; and Compound Interest

3. 4.5/5.5
Solving Exponential and
Logarithmic Equations
• Solve exponential equations.
• Solve logarithmic equations.

4. Solving Exponential Equations
Equations with variables in the exponents, such as
3x = 20 and 25x = 64,
are called exponential equations.
Use the following property to solve exponential
equations.
Base-Exponent Property
For any a > 0, a ≠ 1,
ax = ay ↔ x = y.
Slide 4.5/5.5 - 4

5. Example
Solve 2 3x−7
= 32.
Solution:
Write each side as a power of the same number (base).
2 3x−7 = 2 5
Since the bases are the same number, 2, we can use the
base-exponent property and set the exponents equal:
3 x −7
3x − 7 = 5 Check x = 4: 2 = 32.
3x = 12 2 3(4 )−7 ? 32
x=4 212−7
25
The solution is 4. 32 32 TRUE
Slide 4.5/5.5 - 5

6. Another Property
Property of Logarithmic Equality
For any M > 0, N > 0, a > 0, and a ≠ 1,
loga M = loga N ↔ M = N.
Slide 4.5/5.5 - 6

7. Example
Solve: 3x = 20.
Solution:
3x = 20
This is an exact answer. We
log 3 = log 20
x
cannot simplify further, but we
x log 3 = log 20 can approximate using a
calculator.
log 20
x= ≈ 2.7268
log 3
We can check by finding 32.7268 ≈ 20.
Slide 4.5/5.5 - 7

8. Example
Solve: e0.08t = 2500.
Solution:
e0.08 t = 2500
ln e0.08 t = ln 2500
0.08t = ln(2500)
ln(2500)
t=
0.08
t ≈ 97.8
The solution is about 97.8.
Slide 4.5/5.5 - 8

9. Solving Logarithmic Equations
Equations containing variables in logarithmic
expressions, such as
log2 x = 4 and log x + log (x + 3) = 1,
are called logarithmic equations.
To solve logarithmic equations algebraically, we first try
to obtain a single logarithmic expression on one side and
then write an equivalent exponential equation.
Slide 4.5/5.5 - 9

10. Example
Solve: log3 x = −2. 1
Check: x =
9
Solution:
log 3 x = −2
log 3 x = −2 1
log 3 ? −2
3−2 = x 9
log 3 3−2
1
2
=x −2 − 2 TRUE
3
1
=x 1
9 The solution is .
9
Slide 4.5/5.5 - 10

11. Example
Solve: log x + log (x + 3) = 1.
Solution:
log x + log (x + 3) = 1
log ⎡ x (x + 3)⎤ = 1
⎣ ⎦
x (x + 3) = 101
x + 3x = 10
2
x 2 + 3x − 10 = 0
(x − 2 )(x + 5 ) = 0
x − 2 = 0 or x + 5 = 0
x = 2 or x = −5
Slide 4.5/5.5 - 11

12. Example (continued)
Check x = 2: Check x = –5:
log x + log (x + 3) = 1 log x + log (x + 3) = 1
log 2 + log (2 + 3) ? 1 log (−5 ) + log (−5 + 3) ? 1
log 2 + log 5 FALSE
log (2 ⋅ 5 )
log10
1 1 TRUE
The number –5 is not a solution because negative
numbers do not have real number logarithms. The
solution is 2.
Slide 4.5/5.5 - 12

13. Example
Solve: ln (4x + 6 ) − ln (x + 3) = ln x.
Solution:
ln (4x + 6 ) − ln (x + 3) = ln x 0 = x2 + x − 6
4x + 6 0 = (x + 3)(x − 2 )
ln = ln x
x+5
x + 3 = 0 or x − 2 = 0
4x + 6
=x x = −3 or x = 2
x+5
4x + 6
(x + 5 )⋅ = x (x + 5 ) Only the value 2 checks
x+5 and it is the only solution.
4x + 6 = x 2 + 5x
Slide 4.5/5.5 - 13

14. Example - Using the Graphing Calculator
Solve: e0.5x – 7.3 = 2.08x + 6.2.
Solve:
Graph
y1 = e0.5x – 7.3 and
y2 = 2.08x + 6.2
and use the Intersect
method.
The approximate
solutions are –6.471 and
6.610.
Slide 4.5/5.5 - 14