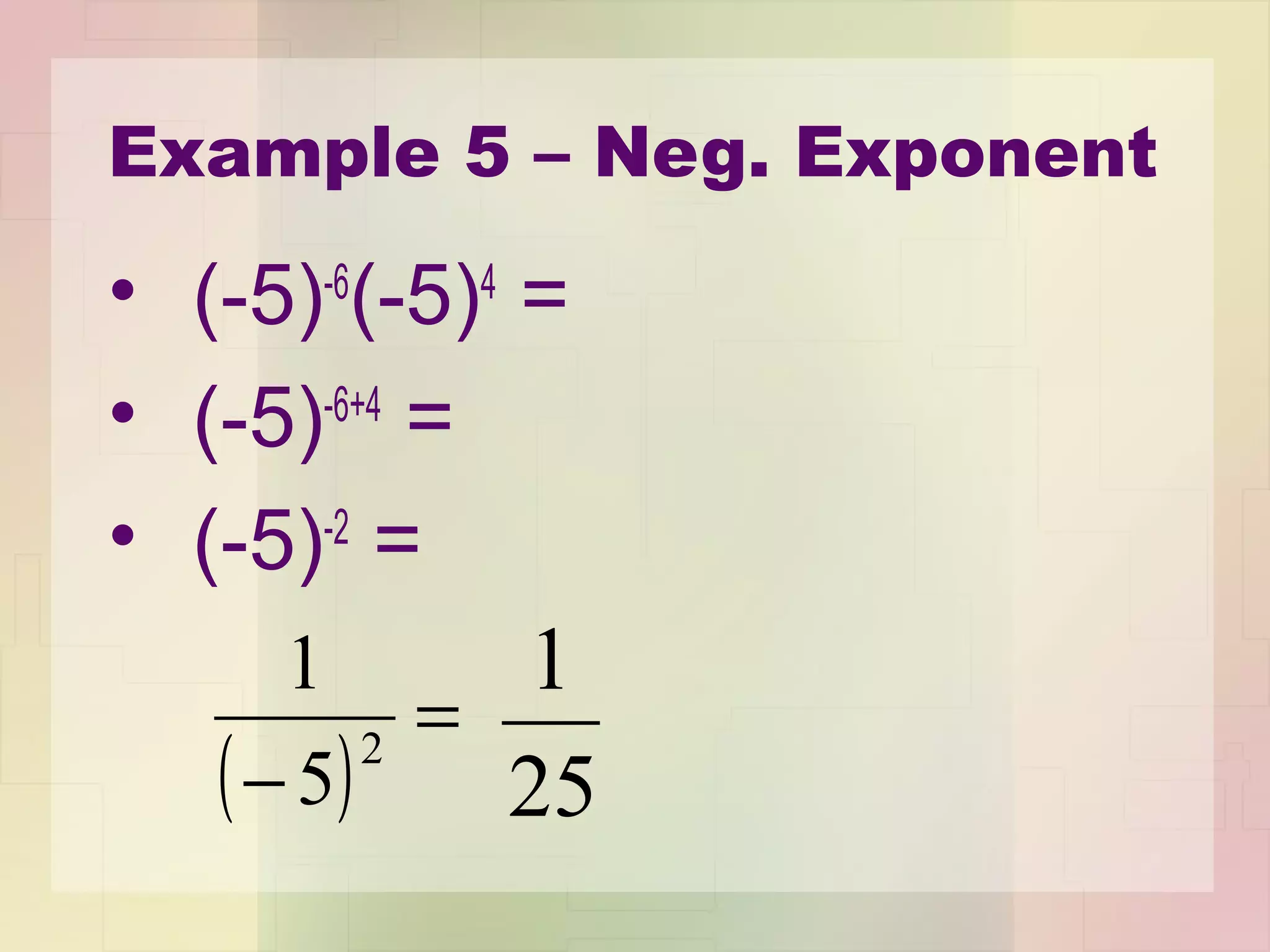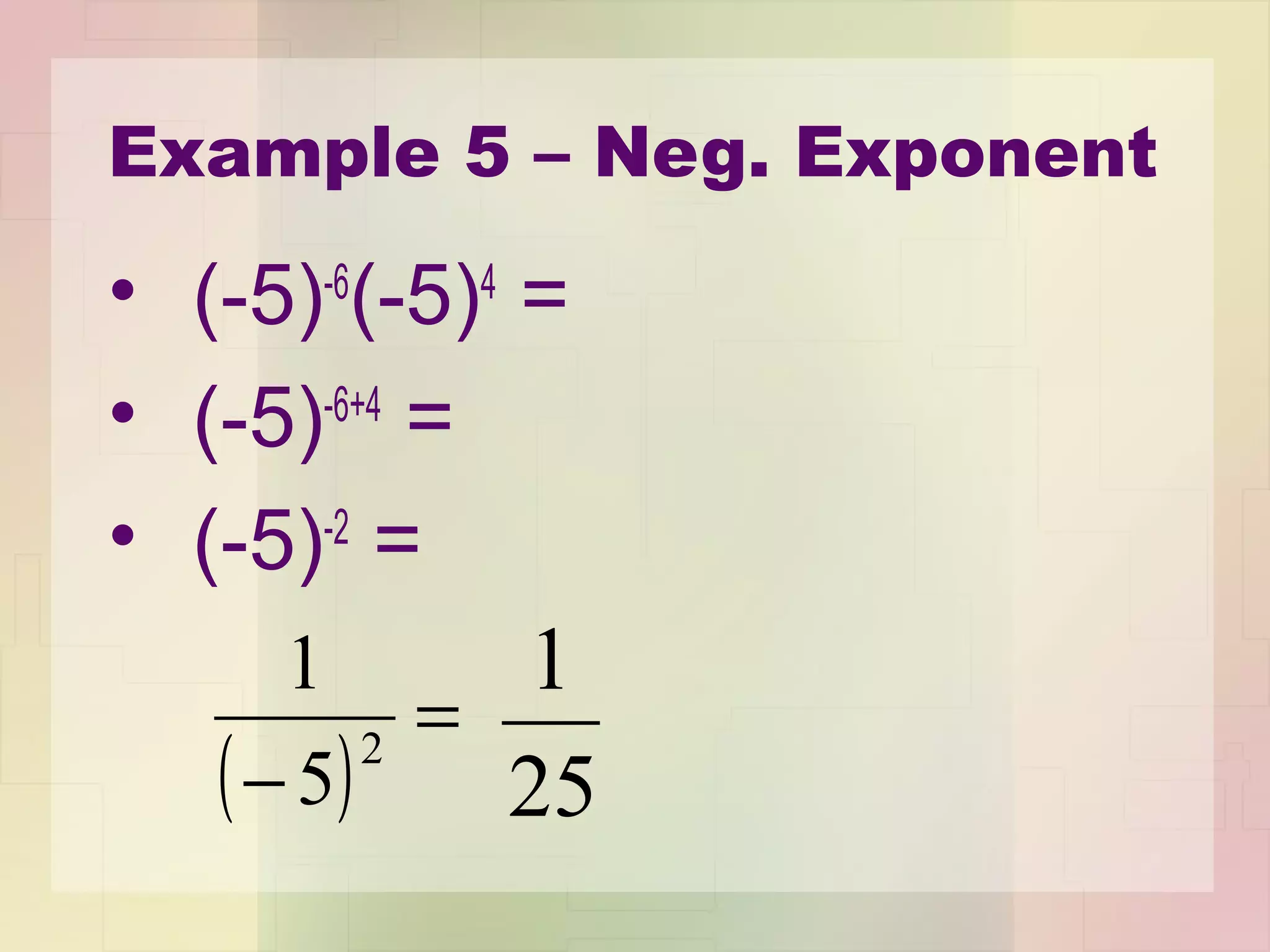
The document summarizes properties of exponents including the product, power, and quotient properties. It provides examples of applying each property to simplify exponential expressions. For example, it shows that the product property allows rewriting (-5)4 * (-5)5 as (-5)4+5 = (-5)9 = -1953125. It also introduces scientific notation and provides an example of rewriting 131,400,000,000 as 1.314 x 1011 by moving the decimal 11 places to the right.

1. 6.1 Using
Properties of
Exponents
p. 323

2. Properties of Exponents
a&b are real numbers, m&n are integers
• Product Property: am
* an
=am+n
• Power of a Power Property: (am
)n
=amn
• Power of a Product Property: (ab)m
=am
bm
• Negative Exponent Property: a-m
= ; a≠0
• Zero Exponent Property: a0
=1; a≠0
• Quotient of Powers: am
= am-n
; a≠0
an
• Power of Quotient: b≠0
m
mm
b
a
b
a
=





m
a
1

3. Example 1 – Product Property
• (-5)4
* (-5)5
=
• (-5)4+5
=
• (-5)9
=
• -1953125

4. Example 2
• x5
* x2
=
• x5+2
=
• x7

5. Example 3 – Power of a Power
• (23
)4
=
• 23*4
=
• 212
=
• 4096

6. Example 4
• (34
)2
=
• 34*2
=
• 38
=
• 6561

7. Example 5 – Neg. Exponent
• (-5)-6
(-5)4
=
• (-5)-6+4
=
• (-5)-2
=
( )
=
−
2
5
1
25
1

8. Example 6 – Quotient of
Powers
=3
5
x
x
=−35
x 2
x

9. Example 7 – Power of
Quotient
=





−
2
5
s
r
( )
=
− 25
2
s
r
=−10
2
s
r 102
sr

10. Example 8 – Zero Exponent
• (7b-3
)2
b5
b =
• 72
b-3*2
b5
b =
• 49 b-6+5+1
=
• 49b0
=
• 49

11. Example 9 – Quotient of
Powers
=10
5
x
x
=−105
x =−5
x 5
1
x

12. Scientific Notation
• 131,400,000,000=
1.314 x 1011
Move the decimal
behind the 1st
number
How many
places did you
have to move
the decimal?
Put that number here!

13. Example – Scientific Notation
• 131,400,000,000 =
• 5,284,000
1.314 x 1011
=
5.284 x 106
611
10*
284.5
314.1 −
900,2410*249. 5
≈≈

14. AssignmentAssignment