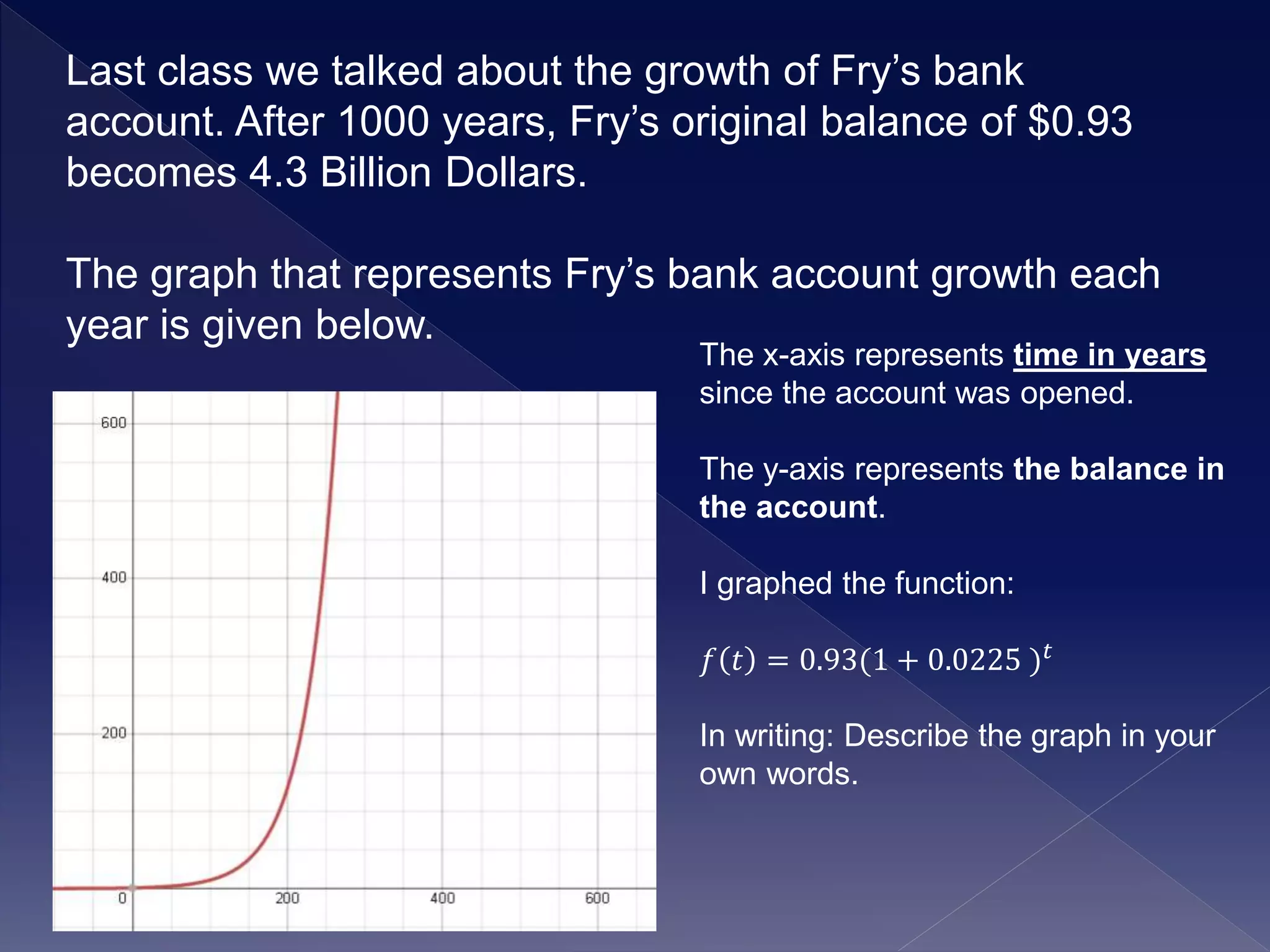
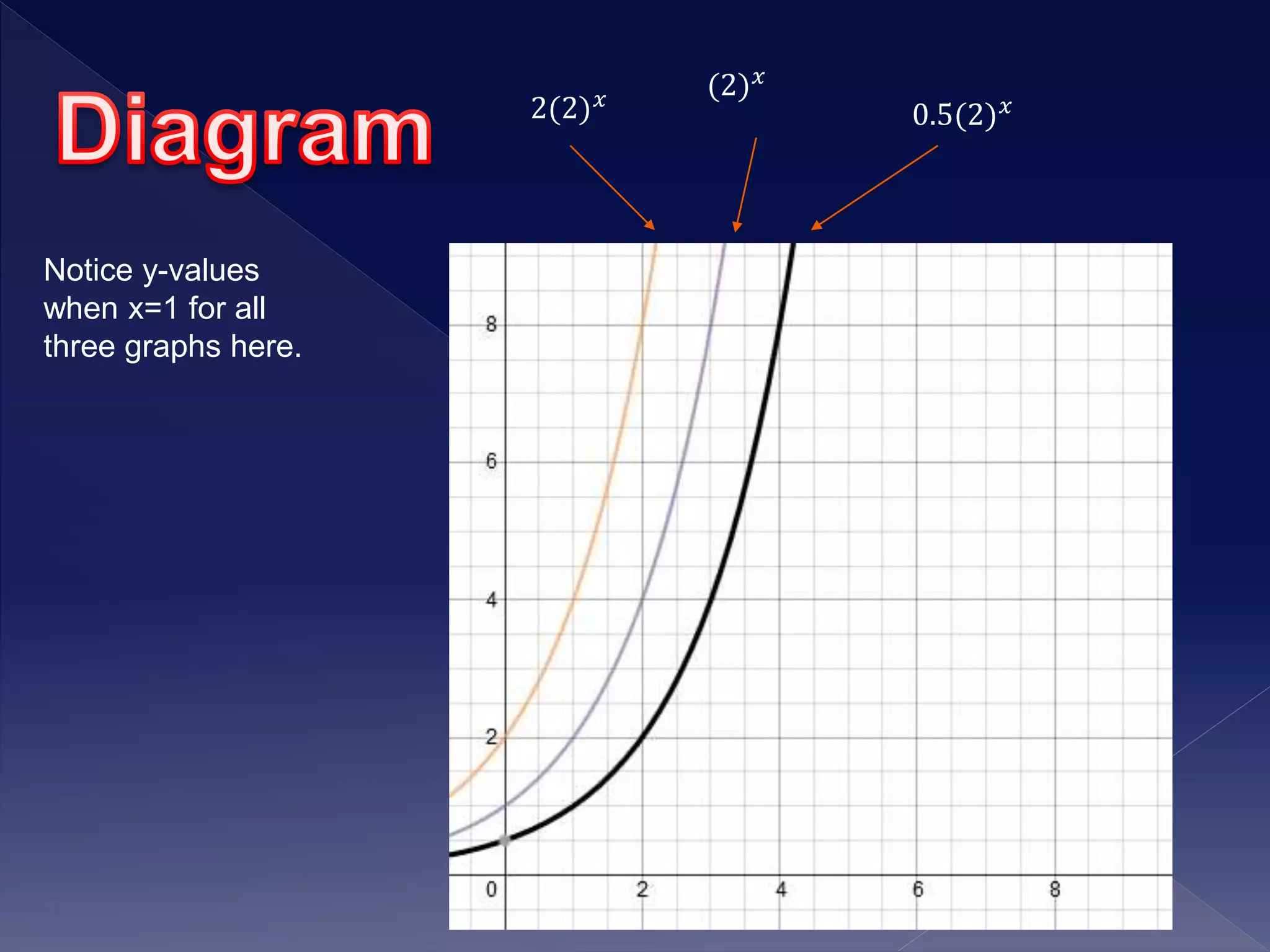
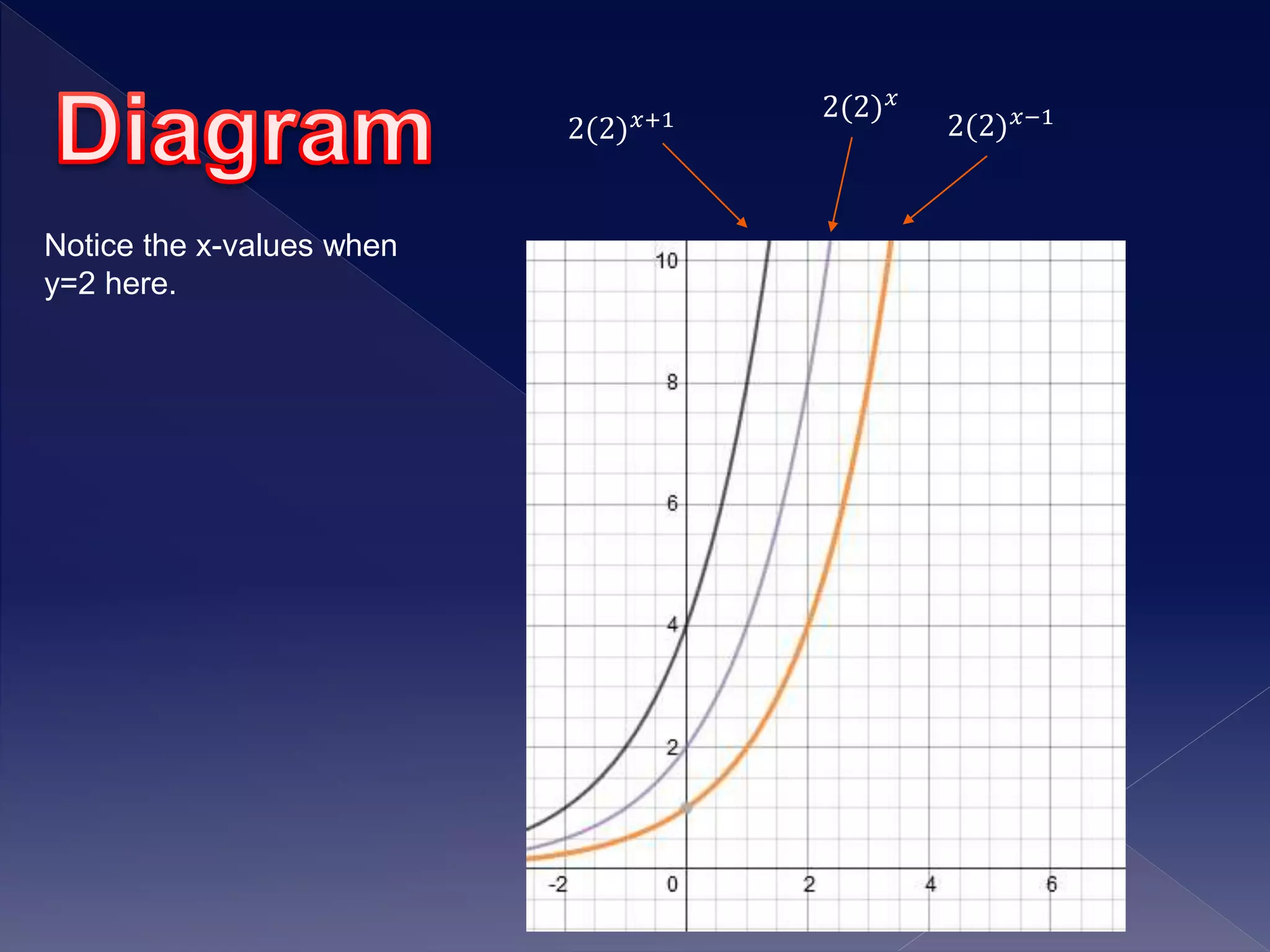
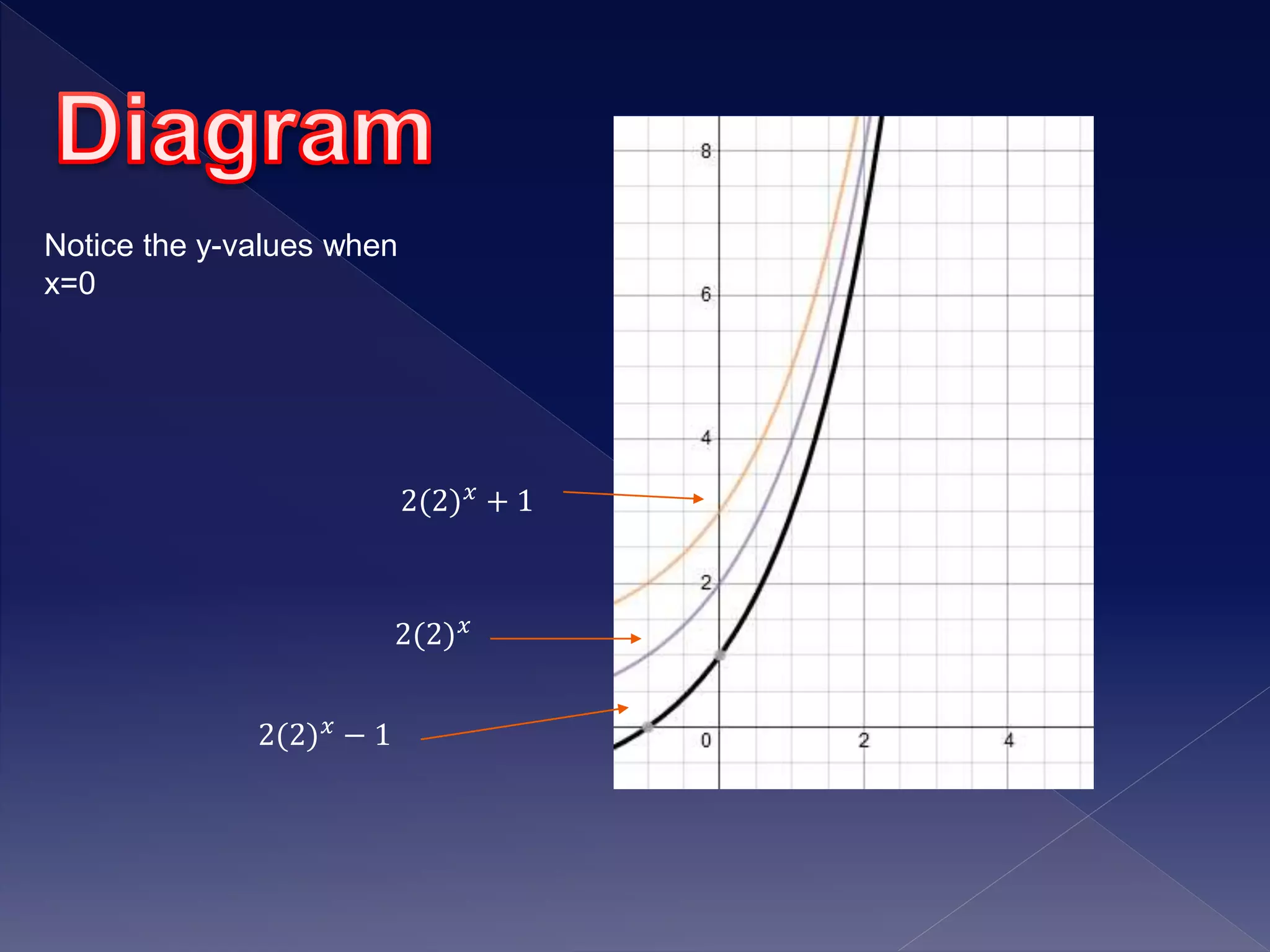
1) The document discusses exponential growth functions and how changing the parameters a, h, and k transforms the graph of the exponential function f(x) = abx-h + k. 2) It explains that changing a stretches or compresses the graph vertically, changing h shifts the graph left or right, and changing k shifts the graph up or down. 3) Examples are given of exponential growth scenarios involving bacteria reproduction and how changes to the starting amount, time, or vertical shift would be represented by transformations to the parameters a, h, and k.

1. QR for lesson:

2. 1) Explain what a savings account is?
2) Why would someone want to have a savings account (as
opposed to a checking account)?
A major reason for having a savings account is that the interest rate
on a savings account is generally higher then a checking account.
Question:
What is interest?

3. Interest is basically the cost of money.
I want to burrow $23,000 from you, money which I don’t have, to buy a car.
Unless you have a generous and very rich family member, $23,000 isn’t money
that is just lying around.
However, you can burrow $23,000 from a bank. In return for the money the bank
gives you, you pay a little bit (or a lot) extra when you pay back the money.
The extra money you pay is called interest.

4. <iframe width="640" height="360"
src="http://www.youtube.com/embed/https:
//youtu.be/GHHesANT6OM?rel=0&start=3
&end=85&autoplay=0" frameborder="0"
allowfullscreen></iframe>

5. Watch the video

6. How much is in Fry’s bank account? Without calculating:
1) Make a guess
2) Give a value that you know for sure is too low
3) Give a value you know for sure is too high
4) Now answer question 1 and 2 in the ‘exponential growth’ worksheet

7.  Exponential Growth is when a quantity grows by the same rate over
the same time period.
For example, Fry’s bank account grows by 2.25% every year (over the
course of 1000 years).
Rather then, calculate year-by-year to find the balance, you can write a
formula:
 To calculate exponential growth you can use the function:
 𝒇 𝒕 = 𝒂(𝟏 + 𝒓) 𝒕
 a = original amount
 r= rate of growth
 t = time
Question: Think back to geometric sequences. Why is the common
ratio, r,(1+r) for exponential growth?

8. Answer question #3 in the worksheet you have started

9. In the last example, we looked at interest that was accumulated once per
year.
One time per year you take your current balance and multiply it by the
interest rate to get your new value.
However….
When a banks compete for your money, they offer interest that
accumulates twice per year, quarterly, and even continuously.
 Compounding interest is interest that is earned over a defined period
of time. The equation is:
 𝒇 𝒕 = 𝒂 𝟏 +
𝒓
𝒏
𝒏𝒕
 a = original amount
 r= rate of growth
 t = time in years
 n = number of times interest compounded per year

10. I get a $1000 graduation gift. Being a savvy investor I get a mutual fund
that pays 3.5% interest over a period of 5 years. The interest on the
mutual fund is compounded monthly. When I graduate college in 5
years, how much will my Mutual Fund be worth?
 Things I know:
 a = $1000 original amount
 r = 0.035
 n = 12 times per year
 t = 5 years
𝑓 𝑡 = 𝑎(1 +
𝑟
𝑛
) 𝑛𝑡
𝑓 𝑡 = 1000(1 +
0.035
12
)12(5)
$1190.94

11. Another mutual fund offers all identical options. However, the interest is
compounded daily instead of monthly. How much will you earn if you go with
the second mutual fund?
 Things I know:
 a = $1000 original amount
 r = 0.035
 n = 365 (because this one is compounded daily)
 t = 5 years
$1191.24
Notice that the difference between the two option is
less then $1. However, when you as an investor
have little two distinguish the two mutual funds by,
the logical better choice is to choose the one which
will give you more money in the long run.
…and all else being equal, the better choice is to
go with the option that has the greatest rate of
compounding.

12. Answer question 4 on the worksheet (all parts).

13. Answer question #5 and #6 on the worksheet and submit.
Watch the video, then..

15. Please download the Desmos app if you do not
already have it.
Open the Exponential Growth Function worksheet
and answer question #1 through #4.

16. Day 1- Learn about specific application of exponential
growth to interest rate with an equation.
Day 2- Learn about exponential growth as a function and
the relationship between the equation and the graph.

17. Last class we talked about the growth of Fry’s bank
account. After 1000 years, Fry’s original balance of $0.93
becomes 4.3 Billion Dollars.
The graph that represents Fry’s bank account growth each
year is given below.
The x-axis represents time in years
since the account was opened.
The y-axis represents the balance in
the account.
I graphed the function:
𝑓 𝑡 = 0.93(1 + 0.0225 ) 𝑡
In writing: Describe the graph in your
own words.

18. Objective:
Describe the transformation of an exponential function graph and its
application to exponential growth problems.

19.  The parent function of an exponential growth function is defined as:
𝑓 𝑥 = 𝑏 𝑥 where |b| > 1
 The general form of an exponential function is:
𝑓 𝑥 = 𝑎𝑏 𝑥−ℎ + 𝑘
Now Answer question #5 on the worksheet (all parts).
The graph used to compare
other graphs to

20. To find out what happens when the exponential parent functions is
transformed let’s suppose that we have a sample of bacteria that like to
double over a certain time.
 𝑓 𝑡 = 2 𝑡 means one bacteria doubles every time interval. (say
every hour). This will be our parent function.
 𝑓 𝑡 = 2(2) 𝑡
means we start with 2 bacteria instead and double it.
 Since a = 2 here the graph of this new function is stretched
vertically by a factor of 2.
 If instead we could cut a bacteria in half and it still reproduced at
the same rate, we would start with a=0.5. This would compress
the function vertically by a factor of ½.

21. 2(2) 𝑥 (2) 𝑥
0.5(2) 𝑥
Notice y-values
when x=1 for all
three graphs here.

22. Now suppose that we have 2 bacteria but half of them die BEFORE they start
to double because of a freeze.
 𝑓 𝑡 = 2(2) 𝑡−1 means we start with 2 bacteria and half of them die before
time starts.
 Here h = 1, this has the effect of shifting your graph to the right 1
 Now suppose the 2 bacteria already doubled before time starts (super
bacteria). In order to adjust, we need to make h= -1 (think of it as 1
hour before normal functions) which has the effect of shifting the graph
to the left 1 unit.
 Another way to think of h is it’s ability to exponentially increase or
decrease your original starting amount by the common ratio (the b-
value).
 If I start with 2 bacteria and h=2, my starting amount would be at
1/2 of a bacteria.

23. 2(2) 𝑥+1 2(2) 𝑥
2(2) 𝑥−1
Notice the x-values when
y=2 here.

24. Finally suppose you put another bacteria in before they start reproducing.
 The function 𝑓 𝑡 = 2(2) 𝑥 + 1 means we put in an extra bacteria
 Here k =1. This has the effect of shifting the graph up 1 unit.
 Suppose instead you take one bacteria out (or one dies) before
they start to reproduce. Here k = -1 and this has the effect of
shifting the graph down one unit.

25. 2(2) 𝑥 − 1
2(2) 𝑥
2(2) 𝑥 + 1
Notice the y-values when
x=0